
par Sylvain Bouley | Jan 12, 2021 | Zoom Sur
La surface de la Terre se réchauffe. Et ce réchauffement est causé par l’accumulation depuis plus d’un siècle de gaz à effet de serre, tel que le CO2, émis par les activités humaines. Voilà près de 30 ans maintenant que ce résultat scientifique fait consensus dans la communauté des physiciens de l’atmosphère et du climat.

Bien sûr, ce résultat questionne aujourd’hui notre mode de vie et le fonctionnement même de notre société [1]. Car sans baisse radicale de nos émissions de gaz à effet de serre, et donc sans changement radical de nos modes de transport et consommation, la surface de la Terre pourrait se réchauffer de 3 à 5°C d’ici à la fin du siècle [2]. Les conséquences de ce réchauffement seraient dramatiques partout sur Terre. Montée des eaux, acidification des océans, modification des zones de précipitation conduisant à l’aridification de nombreuses terres, amplification des événements météorologiques extrêmes, etc.. Un sacré programme …
Modèle climatique du système « Terre »
La démonstration scientifique de ce réchauffement climatique a pour la première fois été proposée dans les années 1960 par le scientifique nippo-américain Syukuro Manabe à l’aide d’un modèle numérique de climat simplifié [3]. L’idée sur le papier est assez simple. À l’aide d’un programme informatique, on simule une Terre « virtuelle » sur un ordinateur en résolvant numériquement les équations physiques principales qui régissent le comportement de l’atmosphère de la Terre : les équations de la convection, de la thermodynamique, du transfert radiatif, etc. On réalise alors une première expérience numérique dans laquelle la quantité de CO2 est choisie égale à celle de la période pré-industrielle (autour de 300 ppm ou partie par million de CO2, c’est-à-dire 0,03% de CO2 dans l’atmosphère) ; puis une seconde dans laquelle la quantité est artificiellement augmentée (par exemple à 600 ppm pour un doublement de la concentration atmosphérique en CO2). Pour référence, la concentration moyenne de CO2 en 2019 est d’environ 410 ppm soit 0,041% [4]. On quantifie alors l’effet du CO2 sur la température moyenne à la surface de la Terre en comparant ces différentes expériences. Dès 1967, Manabe montrait avec son modèle numérique de climat très simplifié (fig. 1) qu’un doublement de la concentration en CO2 dans l’atmosphère de la Terre – par rapport à la période pré-industrielle – pouvait conduire à un réchauffement de la température moyenne de sa surface de l’ordre de 2,5°C.
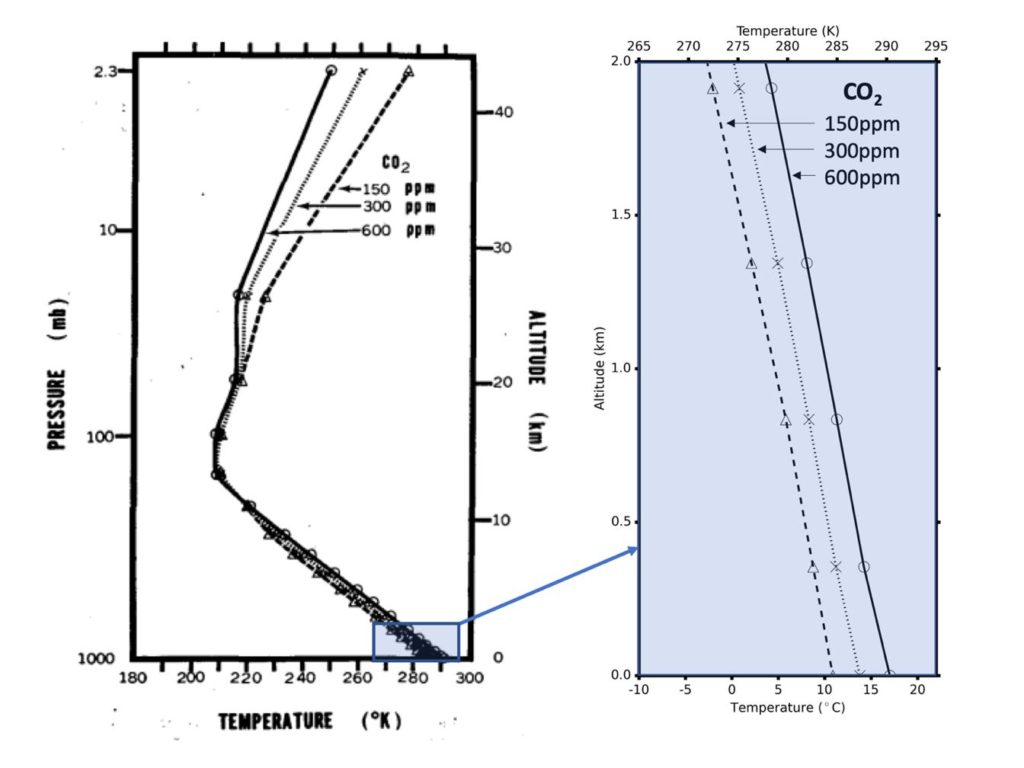
À gauche se trouve un profil vertical de température tel que calculé dans le modèle de Manabe et Wetherald en 1967 [3], pour trois concentrations distinctes en CO2 (150, 300 et 600 ppm ; pour référence, la concentration moyenne de CO2 était d’environ 300ppm à l’aire pré-industrielle, et elle est d’environ 410 ppm en 2019). À droite se trouve un zoom de ce profil vertical de température entre 0 et 2 km. C’est la figure historique montrant pour la première fois, à l’aide d’un modèle d’atmosphère basé sur les composantes physiques majeures du système climatique terrestre (incluant à la fois le transfert radiatif, la convection et une description réaliste des rétroactions de la vapeur d’eau), que l’augmentation de la concentration de CO2 atmosphérique conduit à un réchauffement de la température de surface de la Terre.
Nous sommes maintenant en 2020, soit plus de 50 ans après l’expérience numérique originale de Syukuro Manabe. Si le résultat de cette expérience – c’est à dire que l’augmentation de la quantité de CO2 dans l’atmosphère conduit à un réchauffement important de la température de surface de la Terre – n’a dans le fond pas changé [2], les modèles numériques de climat – eux – ont considérablement évolué. Ces modèles, que l’on appelle maintenant GCM pour Modèle Global de Climat, simulent l’atmosphère de la Terre en trois dimensions et intègrent simultanément tout un ensemble de processus physiques et chimiques très complexes tels que : la mécanique des fluides, le transfert radiatif, la microphysique des nuages, la circulation océanique, l’écoulement des fleuves et rivières, la végétation, etc. Le but ultime de ces modèles est littéralement de prendre en compte simultanément l’effet de tous les processus qui pourraient avoir un impact – même très mineur – sur la surface et l’atmosphère de la Terre. En d’autres termes, le but est de reproduire sur ordinateur une Terre virtuelle qui se comporte de façon aussi proche que possible de notre vraie Terre dans la réalité. Cet effort est nécessaire pour comprendre au mieux l’impact climatique des émissions de CO2 liées à l’utilisation d’énergies fossiles, et ainsi informer les politiques et populations sur les mesures à prendre pour lutter et se préparer contre les conséquences de ce réchauffement climatique.
Les Modèles de Climat Global (GCM) font appel à l’expertise de dizaines de milliers de scientifiques partout dans le monde. Au Laboratoire de Météorologie Dynamique et à l’Institut Pierre et Simon Laplace (LMD/IPSL) où j’ai réalisé ma thèse de doctorat, plusieurs centaines de chercheurs travaillent main dans la main pour développer un tel GCM (fig.2). Pour vous faire une idée, le programme informatique de ce GCM compte près de 150 000 lignes de code, et plus de 40 ans d’expertise accumulée ! Une sacrée usine à gaz dont on doit pourtant comprendre et maîtriser tous les rouages.
Du système « Terre » aux autres planètes
Le GCM du LMD/IPSL a une spécificité quasi unique au monde. Des années 90 à aujourd’hui, il a été progressivement adapté pour étudier le climat de la planète Mars, puis des autres planètes du Système solaire, et enfin des planètes extrasolaires, c’est à dire des planètes qui tournent autour d’autres étoiles que notre Soleil. L’idée géniale ici est d’avoir su tirer avantage du fait que les lois et processus physiques et chimiques qui régissent le fonctionnement de l’atmosphère de la Terre sont basés sur des équations mathématiques universelles, qui sont les mêmes que l’on se trouve sur Terre, sur Mars ou bien sur une exoplanète. Tenez par exemple, les vents atmosphériques peuvent être tout aussi bien décrits par les équations de Navier Stokes de l’hydrodynamique que l’on soit sur Terre ou … sur l’exoplanète « Jupiter chaud » 51 Pegasi b2 ! Idem pour les équations de Clausius-Clapeyron de la thermodynamique, ou encore pour les équations du transfert radiatif.
Les équations de « Navier Stokes » de la mécanique des fluides permettent de décrire le mouvement des masses d’air de l’atmosphère. Elles permettent par exemple d’estimer l’intensité et la direction des grands courants atmosphériques tels que les alizées ou les vents d’Ouest.
Les équations de « Clausius-Clapeyron » de la thermodynamique permettent de décrire l’évolution de la pression de changement d’état d’un gaz en fonction de sa température. Elles permettent par exemple d’estimer les conditions pour lesquelles la vapeur d’eau présente dans l’atmosphère va se condenser, produisant ainsi des nuages et des précipitations.
Les équations du transfert radiatif permettent de décrire comment les gaz et nuages de l’atmosphère interagissent avec la lumière. Les gaz et nuages peuvent absorber la lumière, la réfléchir ou encore en émettre. Les équations du transfert radiatif permettent par exemple de comprendre comment un gaz comme le CO2 interagit avec la lumière, produisant ainsi un effet de serre.
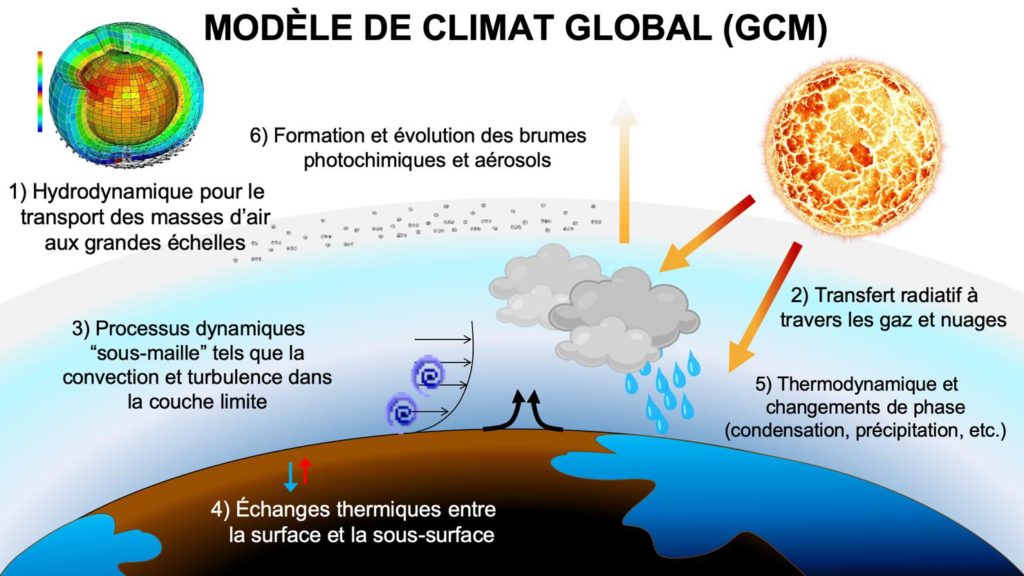
Figure 2: Schéma simplifié illustrant les processus physiques et chimiques principaux qui sont modélisés dans le modèle de climat global (GCM) du LMD/IPSL pour simuler l’atmosphère de la Terre, des planètes du Système solaire et des exoplanètes. Les processus « sous-maille » (en 3) font référence à tous les processus qui ont lieu à des échelles spatiales trop petites pour être directement résolues par le modèle. Crédit : M. Turbet/N. Chaniaud.
Dans la pratique, l’idée a consisté à « hacker » c’est-à-dire adapter le programme informatique simulant la Terre, d’abord en y modifiant tous les paramètres qui lui sont propres (gravité, rayon, relief, niveau d’insolation, composition chimique de l’atmosphère, etc.) et ensuite en y adaptant la formulation de certains processus. Prenons l’exemple de Titan, une lune de Saturne, pour y voir plus clair. Si vous voulez simuler l’atmosphère de Titan, il faut d’abord adapter le GCM à la gravité de Titan (14% de la gravité terrestre), son rayon (40% du rayon terrestre), son niveau d’insolation (1% de l’insolation sur Terre), l’épaisseur et la composition chimique de son atmosphère (1,47 fois la pression de l’atmosphère terrestre ; atmosphère composée essentiellement d’azote N2, de quelques % de méthane CH4, et d’hydrocarbures plus lourds en quantité minoritaire), etc. Dans un second temps, il faut également adapter certains des processus. Titan possède en effet une atmosphère épaisse d’azote et de méthane qui est si froide que le méthane, l’éthane et d’autres hydrocarbures plus lourds peuvent s’y condenser. Oui, il pleut littéralement du pétrole sur Titan. Pour simuler le cycle hydrologique sur Titan (non pas de l’eau comme sur Terre, mais du méthane CH4, de l’éthane C2H6, et des hydrocarbures plus lourds), il convient donc d’adapter les processus thermodynamiques de condensation et précipitation de l’eau vers ceux du méthane, de l’éthane et des hydrocarbures plus lourds.
D’abord, les planètes du Système solaire
Ces Modèles de Climat Global (GCM) donnent aujourd’hui des résultats très satisfaisants. D’abord ils permettent de reproduire fidèlement le comportement de la plupart des atmosphères des planètes du Système solaire, notamment des planètes telluriques (Terre, Mars, Vénus), planètes naines (Pluton) et lunes (Titan, Triton) qui ont une atmosphère. Pour la petite histoire, le GCM du LMD/IPSL de la planète Mars est même utilisé par les grandes agences spatiales (Nasa, Esa, Agence Spatiale Chinoise, etc.) pour préparer les missions d’insertion en orbite et d’atterrissage sur la planète Mars3. Ces mêmes modèles de climat global peuvent également servir à faire de belles découvertes scientifiques, parmi lesquelles : la démonstration de l’origine du « cœur » de glace d’azote de Pluton [5] ; ou encore la démonstration que les périodes passées de forte obliquité sur Mars ont conduit à des cycles de climat glaciaires qui permettent d’expliquer pourquoi les régions proches de l’équateur de Mars sont couvertes de traces d’érosion glaciaire relativement récentes [6].
Pour les planètes géantes du Système solaire (Jupiter, Saturne, Uranus, Neptune), la tâche est un peu plus difficile. Notamment parce que pour simuler correctement la circulation atmosphérique de grandes planètes en rotation rapide4, il est nécessaire d’augmenter significativement la résolution spatiale des simulations numériques5 ce qui augmente considérablement la puissance de calcul nécessaire pour réaliser des simulations numériques 3-D. Toutefois, des résultats récents montrent qu’avec une puissance de calcul importante à disposition, il est possible de reproduire fidèlement les structures atmosphériques des planètes géantes du Système solaire [7].
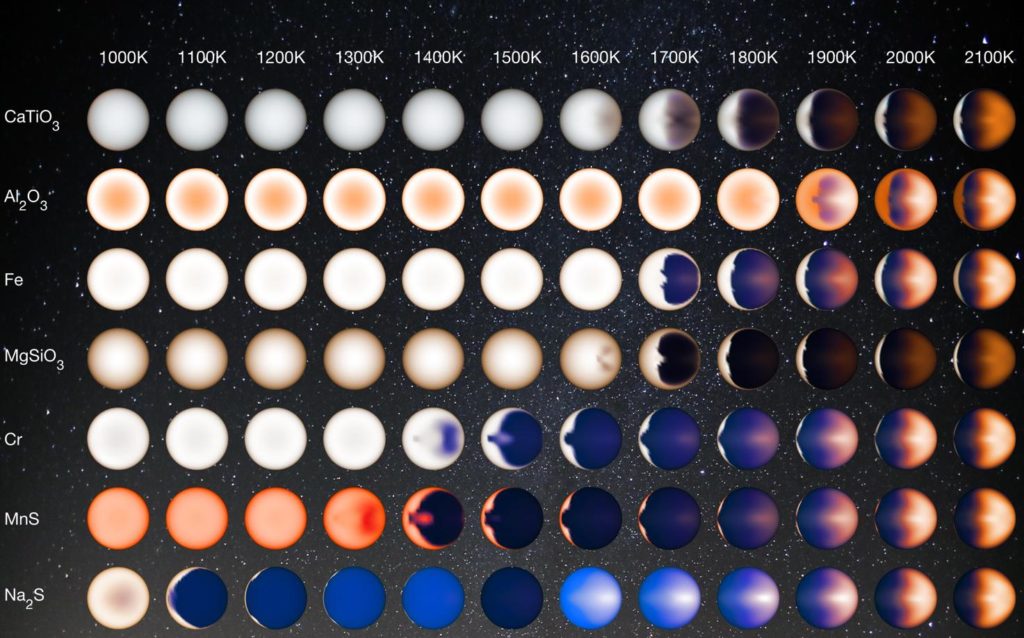
Cette image illustre comment l’apparence et les couleurs de la face illuminée (face jour uniquement ; la face nuit n’est pas montrée) d’une exoplanète « Jupiter chaud » varient en fonction de sa température et de la composition de ses nuages, aussi exotiques soient-ils. Cette illustration a été réalisée à partir de simulations numériques 3-D [10] utilisant le SPARC/MIT GCM. Crédit : NASA/JPL-Caltech/University of Arizona/V. Parmentier.
Ensuite, les planètes extrasolaires
L’utilisation de modèles de climat global (GCM) a permis également de faire des avancées scientifiques majeures dans le domaine des exoplanètes. Appliqués aux plus grosses et chaudes planètes que nous connaissons – les « Jupiters chauds » –, ils ont permis de comprendre le fonctionnement de régimes de circulation atmosphérique exotiques (Figure 3). D’expliquer notamment comment la redistribution de chaleur s’opère au sein de l’atmosphère en fonction de l’insolation reçue par les planètes [8,9,10], et d’élucider par exemple pourquoi le point le plus chaud de certaines de ces exoplanètes est parfois largement décalé par rapport au point le plus irradié [8,9]. Appliqués aux exoplanètes de taille intermédiaire « super-Terre » ou « mini-Neptune », ces GCMs ont permis d’élucider pourquoi nombre de ces planètes semblent être couvertes d’une épaisse couche de nuages qui empêche nos télescopes de sonder en détail ce qu’il s’y cache [11]. Enfin, appliqués aux petites planètes tempérées – celles qui sont pour l’instant trop petites et trop froides pour être directement accessibles aux techniques de caractérisation d’atmosphère que nous avons à disposition – ces GCMs permettent d’identifier la gamme de toutes les compositions atmosphériques possibles. Cela permet d’être en mesure de reconnaître les différents types d’atmosphères des petites planètes tempérées lorsque ces observations seront un jour possibles [12].
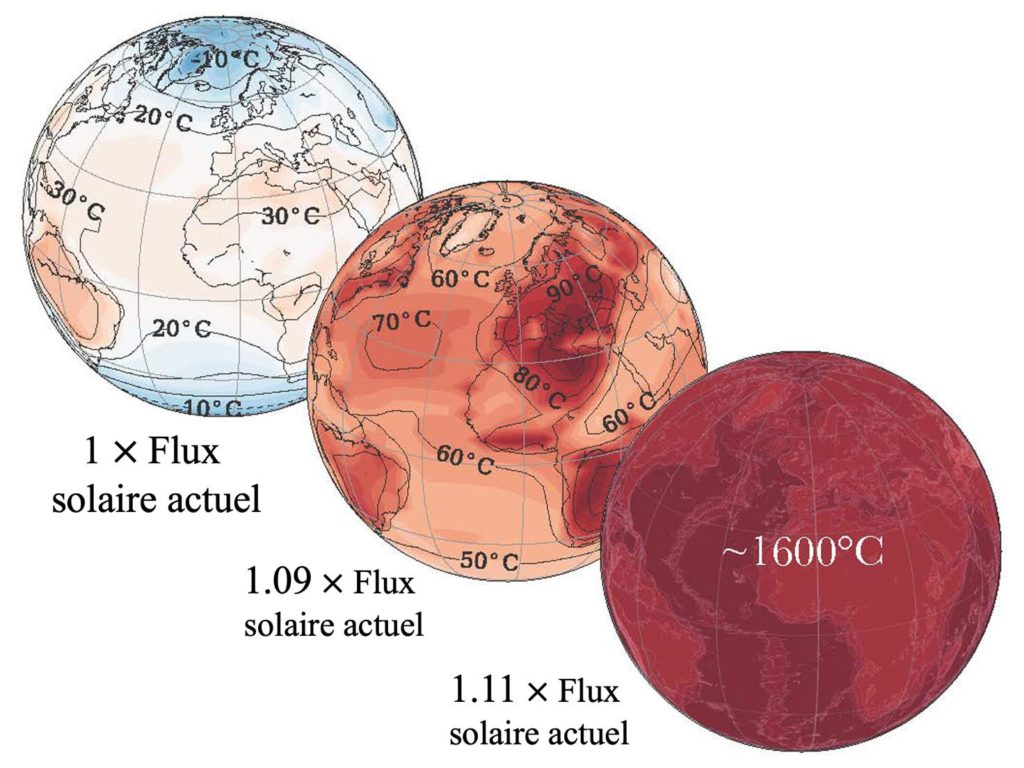
Cartes de températures moyennes annuelles simulées sur Terre pour différentes insolations hypothétiques (1´, 1,09´ et 1,11´ le flux solaire actuel sur Terre) en utilisant le LMD/IPSL GCM [13]. Les insolations simulées correspondent respectivement à l’insolation actuelle, et celles estimées dans 850 et 1150 millions d’années. Crédit : J. Leconte.
Utiliser les exoplanètes pour mieux comprendre la Terre
Si toutes ces avancées scientifiques majeures dans la modélisation numérique des atmosphères des exoplanètes peuvent aujourd’hui voir le jour, c’est grâce à tout le travail réalisé depuis des décennies par les physiciens de l’atmosphère et du climat de la Terre et sur lequel elles s’appuient. Mon grand espoir, c’est celui de pouvoir un jour directement utiliser ce que l’on aura appris des exoplanètes pour aider en retour à mieux comprendre le fonctionnement et l’évolution du climat de la Terre.
Un peu comme on étudie les animaux pour en apprendre plus sur la médecine et le corps humain, étudier les exoplanètes permettrait de replacer la Terre dans un contexte plus large afin de mieux comprendre comment elle s’est formée, a évolué, et va évoluer. Avec l’avènement de nouvelles générations de télescopes et d’instruments ainsi qu’avec l’aide de techniques observationnelles toujours plus innovantes, cette idée pour l’instant un peu théorique – presque philosophique – va commencer à avoir des applications concrètes. Je vais essayer dans les lignes suivantes de vous le démontrer via un exemple sur lequel j’ai personnellement travaillé.
Pour cela, commençons par faire une expérience de pensée très simple. Imaginez que l’on prenne la Terre et la rapproche de quelques pourcents seulement du Soleil. L’augmentation du flux lumineux qu’elle reçoit va chauffer sa surface et donc augmenter sa température. Les océans et mers de la Terre, réchauffés, vont évaporer plus d’eau. La vapeur d’eau étant un puissant gaz à effet de serre, la température de surface de la Terre va continuer d’augmenter. Si le flux solaire reçu par la planète est alors suffisamment grand (autour de 10% de plus que le flux solaire actuel sur Terre [13]), il a été montré indépendamment par plusieurs équipes internationales que l’évaporation des océans devrait s’emballer jusqu’à leur assèchement complet [13,14,15]. Cela provient du fait que l’atmosphère très riche en vapeur d’eau est très opaque au rayonnement infrarouge thermique. La température de la surface doit alors augmenter jusqu’à plus de 1600°C pour pouvoir rayonner dans le visible où la vapeur d’eau laisse passer le rayonnement infrarouge, ce qui est nécessaire pour générer une source de refroidissement. On appelle ce mécanisme d’emballement le « runaway greenhouse » ou « effet de serre galopant ». Ce mécanisme est illustré par des simulations numériques sur la figure 4.
Dans 1 milliard d’années environ, la Terre recevra approximativement 10% de plus que le flux solaire actuel6, ce qui est en théorie suffisant pour que le mécanisme d’effet de serre galopant se mette en place … En fait, certaines études ont montré qu’une augmentation importante de la concentration de CO2 dans l’atmosphère de la Terre pourrait jouer le même rôle qu’une augmentation du flux solaire, et ainsi conduire également à un emballement de l’effet de serre de la vapeur d’eau [14]. Les quantités de CO2 nécessaires pour démarrer cet emballement sont certes en théorie bien supérieures aux prévisions d’émissions anthropiques de CO2 dans l’atmosphère de la Terre. Mais que faire pour en avoir le cœur net ?

Cartes de températures moyennes annuelles simulées sur Terre pour différentes insolations hypothétiques (1´, 1,09´ et 1,11´ le flux solaire actuel sur Terre) en utilisant le LMD/IPSL GCM [13]. Les insolations simulées correspondent respectivement à l’insolation actuelle, et celles estimées dans 850 et 1150 millions d’années. Crédit : J. Leconte.
À l’aide de modèles numériques de climat, j’ai montré très récemment avec mes collègues [15] que cette transition de l’« effet de serre galopant » peut conduire à une augmentation de la taille des planètes pouvant atteindre plusieurs centaines voire milliers de km (jusqu’à plusieurs dizaines de % du rayon de la planète) suite à l’expansion de leur atmosphère très chaude et riche en vapeur d’eau (fig. 5). Pour une planète similaire à la Terre, cette augmentation pourrait atteindre 500 km7. Cela provient d’abord du fait que l’atmosphère riche en vapeur d’eau serait alors beaucoup plus épaisse (d’un facteur 270 par rapport à l’atmosphère terrestre actuelle) ; et ensuite du fait que l’atmosphère serait beaucoup plus chaude donc beaucoup plus dilatée et étendue.
À mesure que l’on découvre un nombre significatif d’exoplanètes similaires à la Terre (en masse et taille), on va pouvoir commencer à tester l’existence et l’impact de l’« effet de serre galopant » sur ces exoplanètes. En particulier, comme l’illustre la figure 6, une augmentation statistiquement significative du rayon des exoplanètes de masse terrestre – à mesure que l’on augmente l’insolation qu’elles reçoivent au-delà de la limite théorique de l’effet de serre galopant ou « runaway greenhouse » – validerait non seulement l’existence du processus d’augmentation de rayon. Mais surtout, elle permettrait de mesurer l’insolation exacte à laquelle a lieu cet emballement. Cette mesure astronomique pourrait permettre – grâce aux exoplanètes – d’évaluer empiriquement à quel point la Terre est proche ou non de cette limite de l’effet de serre galopant. Afin d’avoir le cœur net sur ce qui attend notre Terre dans le futur.
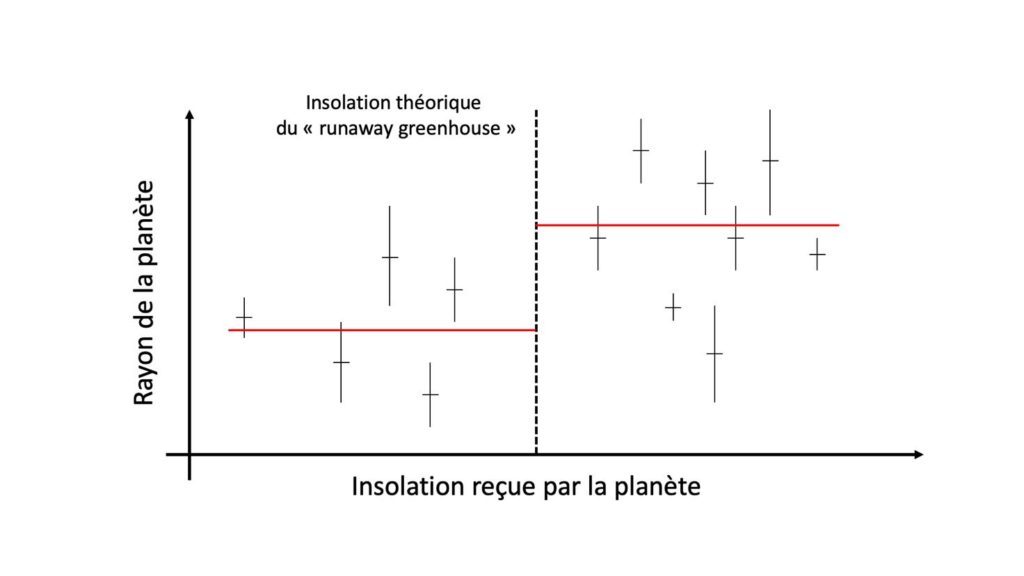
Principe de la mesure statistique de l’effet de serre galopant. On place sur ce diagramme la position (insolation et rayon de la planète) connue de planètes de masse similaire à la Terre (par exemple de 0,5 à 2 masses terrestres. Ces planètes sont indiquées pour l’exemple par des croix noires (barres d’erreur fictives). Si une fraction significative des planètes de l’échantillon est riche en eau, et si le mécanisme d’augmentation de rayon par l’effet de serre galopant ou ‘runaway greenhouse’ de la vapeur d’eau est bien réel, on devrait observer une augmentation statistique (indiquée par la ligne rouge) du rayon des planètes plus irradiées que la limite de l’effet de serre galopant (indiquée par une ligne noire pointillée verticale), par rapport à celles qui le sont moins. Cette mesure astronomique pourrait permettre d’évaluer à quel point la Terre est proche ou non de la limite de l’effet de serre galopant.
Martin Turbet, Observatoire de Genève
Notes (en exposant dans le texte)
[1] Les curieux auront noté que la partie supérieure de l’atmosphère, quant à elle, décroit en température avec l’augmentation de la concentration du CO2. Dans cette partie de l’atmosphère, moins dense, les échanges d’énergie sont dominés par les échanges radiatifs. Le CO2 qui absorbe fortement dans l’infrarouge est également – d’après la loi du rayonnement de Kirchhoff – un très bon émetteur dans l’infrarouge. Dans la partie radiative/haute de l’atmosphère, l’ajout de CO2 va donc augmenter l’émission thermique de l’atmosphère, ce qui conduit à son refroidissement.
[2] 51 Pegasi b est la première planète extrasolaire à avoir été découverte (en 1995). Ce qui a valu entre autre aux astronomes suisses Michel Mayor et Didier Queloz le prix Nobel de physique 2019.
[3] Vous pouvez vous aussi l’utiliser en vous connectant sur http://www-mars.lmd.jussieu.fr/mcd_python/ (en anglais).
[4] La vitesse de rotation à l’équateur est environ 22 fois plus grande sur Saturne (et 27 fois sur Jupiter) que sur Terre.
[5] Il existe une échelle caractéristique – que l’on appelle « rayon de déformation de Rossby » – pour laquelle les effets de la rotation planétaire sont aussi importants que ceux de la gravité ou des forces de pression. Pour représenter correctement l’effet de la rotation planétaire (à l’origine des jets de Jupiter, par exemple ; ou encore de la circulation de Hadley sur Terre), il est nécessaire que la résolution spatiale d’une simulation numérique 3-D soit plus fine que le rayon de déformation de Rossby. La résolution spatiale (en km) doit donc être d’autant plus fine que la planète simulée est grande et tourne rapidement sur elle-même. D’où la difficulté à simuler correctement la circulation atmosphérique sur une planète comme Jupiter.
[6] Le mécanisme moteur qui permet au Soleil d’alimenter la Terre en énergie lumineuse est la fusion nucléaire. À mesure que les atomes d’hydrogène fusionnent, des éléments plus lourds comme de l’Hélium se forment. Au cours du temps, la proportion d’Hélium dans le cœur du Soleil augmente. Le noyau du Soleil devient de plus en plus dense et de plus en plus chaud. Les réactions nucléaires s’y font alors plus intenses. Résultat : La luminosité du Soleil augmente avec le temps et sera environ 10% plus grande d’ici environ 1 milliard d’années.
[7] Pour la comparaison, l’épaisseur typique de l’atmosphère terrestre est de ~10km, en fonction de la longueur d’onde/couleur à laquelle on l’observe.
Bibliographie
[1] Premier rapport d’évaluation du GIEC, 1990.
[2] Cinquième rapport d’évaluation du GIEC, 2014.
[3] S. Manabe & R.T. Wetherald, « Thermal Equilibrium of the Atmosphere with a Given Distribution of Relative Humidity », Journal of Atmospheric Sciences Volume 24 (1967).
[4] Concentration de CO2 mesurée à l’Observatoire du Mauna Loa, à Hawaii (Etats-Unis), Scripps CO2 Program.
[5] T. Bertrand & F. Forget, « Observed glacier and volatile distribution on Pluto from atmosphere- topography processes », Nature Volume 540 (2016).
[6] F. Forget, R. M. Haberle, F. Montmessin, B. Levrard, & J. W. Head, « Formation of Glaciers on Mars by Atmospheric Precipitation at High Obliquity », Science Volume 311 (2006).
[7], A. Spiga et al., « Global climate modeling of Saturn’s atmosphere. Part II: Multi-annual high-resolution dynamical simulations », Icarus Volume 335 (2020).
[8] T.D. Komacek, A.P. Showman & X. Tan, « Atmospheric Circulation of Hot Jupiters: Dayside-Nightside Temperature Differences. II. Comparison with Observations », The Astrophysical Journal Volume 835 (2017).
[9] V. Parmentier & I.J. Crossfield, « Exoplanet Phase Curves: Observations and Theory », Handbook of Exoplanets, Springer International Publishing AG (2018).
[10] V. Parmentier et al., « Transitions in the Cloud Composition of Hot Jupiters », The Astrophysical Journal, Volume 828 (2016).
[11] B. Charnay, V. Meadows, A. Misra, J. Leconte & G. Arney, « 3D Modeling of GJ1214b’s atmosphere: Formation of inhomogeneous high clouds and observational implications », The Astrophysical Journal Letters Volume 813 (2015).
[12] M. Turbet et al., « The habitability of Proxima Centauri b. II. Possible climates and observability », Astronomy & Astrophysics Volume 596 (2016).
[13] J. Leconte, F. Forget, B. Charnay, R. Wordsworth & A. Pottier, « Increased insolation threshold for runaway greenhouse processes on Earth-like planets », Nature Volume 504 (2013).
[14] C. Goldblatt, T.D. Robinson, K.J. Zahnle & D. Crisp, « Low simulated radiation limit for runaway greenhouse climates », Nature Geoscience Volume 6 (2013).
[15] M. Turbet, D. Ehrenreich, C. Lovis, E. Bolmont & T. Fauchez, « The runaway greenhouse radius inflation effect. An observational diagnostic to probe water on Earth-sized planets and test the habitable zone concept », Astronomy & Astrophysics Volume 628 (2019).

par Sylvain Bouley | Jan 12, 2021 | Actualités
Coalescence d’un trou noir de 23 masses solaires avec un astre compact 9 fois plus léger et de nature inconnue

Les détecteurs Virgo (USA) et LIGO (Italie) ont enregistré le 14 août 2019 des ondes gravitationnelles (des déformations de l’espace-temps) dont la fréquence est montée de 20 à 100 Hz environ en deux secondes. Leur analyse a révélé qu’elles ont été émises durant les dernières secondes avant la fusion de deux astres en un seul plus massif . Ce couple d’astres, avant qu’il fusionne en un trou noir plus massif de 25,6 masses solaires, était formé d’un astre compact de 2,6 masses solaires et d’un trou noir de 23,2 masses solaires. Aucune contrepartie connue à ce jour n’a été observée dans le spectre électromagnétique (lumière visible, ondes radio, rayons X et gamma).
Mais au fait, direz-vous, si on additionne les masses des deux astres, on trouve 2,6+23,2=25,8. Or l’astre final a une masse de 25,6 masses solaires. Où sont passées les 0,2 masses solaires manquantes ? Elles ont été converties en énergie, selon la célèbre formule E=mc**2, précisément celle qui a propagé des déformations d’espace-temps sous forme d’ondes gravitationnelles.
Cet événement présente deux particularités intéressantes.
D’abord la masse du corps le plus léger, 2,6 masses solaires, en fait soit le trou noir le moins massif jamais observé, soit l’étoile à neutrons la plus massive connue. En principe, rien ne s’oppose à l’existence d’un trou noir de 2,6 masses solaires, mais les scénarios actuels de l’effondrement des étoiles massives suggèrent qu’on obtienne, outre les quantités énormes de matière éjectées dans l’espace, des trous noirs plus massifs. En ce qui concerne les étoiles à neutrons, tous les modèles actuels décrivant les propriétés de leur matière (équations d’état), quoique nombreux et tous relativement spéculatifs, prévoient pour les étoiles à neutrons une masse maximale n’excédant 2 masses solaires que de très peu.
L’autre intérêt est la grande différence de masses entre les deux astres au moment où ils ont émis ces ondes gravitationnelles. Une onde gravitationnelle émise par deux astres de même masse est surtout intense à une certaine fréquence, que l’on peut appeler la fréquence fondamentale du système. Deux astres de masses très différentes émettent, en plus de ce mode fondamental, des ondes gravitationnelles à des fréquences multiples du mode fondamental. Si on faisait un parallèle avec la musique, on dirait que les systèmes asymétriques ont un timbre plus riche que les systèmes formés de deux astres de même masse. Cela offre des contraintes nouvelles pour mettre à l’épreuve la théorie de la relativité générale en champ gravitationnel fort, ainsi que les théories alternatives. Encore une fois, on ne mesure pas de déviation entre ce qui est prédit par la théorie de la relativité générale et ce qui est observé.
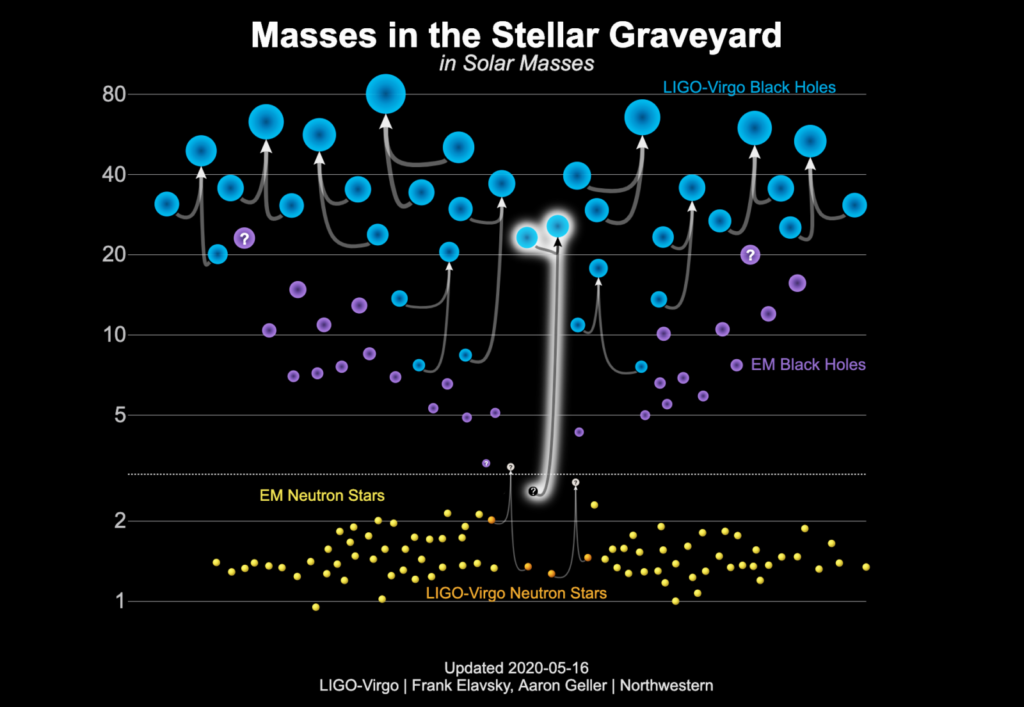
masse des objets observés par LiGo-Virgo. Les fusions d’étoiles sont indiquées par des lignes partant des deux étoiles progénitrices et aboutissant (flèche) à l’étoile fusionnée. Les objets en jaune sont des étoiles à neutrons dont la masse a pu être mesurée par des observations dans le domaine électromagnétique (donc pas avec LiGo-Virgo). Les étoiles à neutrons détectées avec des ondes gravitationnelles (avec LiGo et/ou Virgo) sont en orange. Les objets en violet sont des trous noirs détectés dans le domaine électromagnétique, ceux en bleu sont des trous noirs détectés grâce aux ondes gravitationnelles. LiGo-Virgo a observé deux fusions d’étoiles à neutrons, onze fusions de trous noirs, et l’événement GW190814 (entouré en blanc), fusion entre un trou noir et un objet de nature inconnue. L’auteur parle de «stellar graveyard», soit «cimetière d’étoiles» pour ce objets.
Fabrice Mottez, CNRS, Observatoire de Paris-psl
Lien vers l’article de la découverte : https://ui.adsabs.harvard.edu/abs/2020arXiv200612611T/abstract

par Sylvain Bouley | Jan 12, 2021 | Sur le Terrain

Une Gestation Difficile
Le projet de création d’une association continentale d’astronomie professionnelle est une idée ancienne qui a eu une genèse plutôt laborieuse. L’appel à sa création remonte à 2008 lorsque Peter Martinez (Afrique du Sud) et Pius Okeke (Nigéria) ont discuté dans divers articles des moyens de développer l’astronomie en Afrique, en appelant spécifiquement à la formation d’une société panafricaine d’astronomie. Entre temps, des sociétés régionales d’astronomie professionnelle ont été créées en Afrique de l’Ouest et en Afrique de l’Est. Notons aussi que lors du lancement en 2010 de la société africaine de physique à Dakar, un certain nombre d’astronomes de tout le continent et de la diaspora africaine ont relancé l’idée de former une société africaine d’astronomie. Suite à cette réunion, s’est tenue la rencontre de Ouagadougou en 2010, lors de laquelle fut élaborée une première copie d’une constitution pour une telle société d’astronomie (AfAS), tâche qui fut achevée en janvier 2011. L’AfAS a finalement été inaugurée lors de la deuxième réunion régionale du MEARIM meeting de l’IAU pour l’Afrique et le Moyen-Orient à Cape Town en Afrique du Sud en avril 2011.

Fig1: La réunion de création de l’AfAS en mars 2018 à l’observatoire historique de Cape Town
Espoirs Déçus et Lancement d’ AfAS2.0
Malheureusement, pas grand chose ne se passa concrètement pendant les années suivantes; aussi un consensus se dégagea après plusieurs concertations, dont l’initiative des astronomes réunis lors de la réunion d’Addis-Abeba en 2017, de déclarer morte la structure précédente et de lancer l’AfAS 2.0, dans un nouveau cadre et avec notamment la nécessité de bénéficier d’un soutien institutionnel fort. C’était ce soutien qui semblait manquer dans la précédente structure.
Le gouvernement Sud African à travers la DSI (Department of Science and Innovation) proposa d’héberger la structure et de la financer pour les premières années. Un colloque fut organisé à ce propos à Cape Town en mars 2018, avec la participation de quelques soixante astronomes d’Afrique et de la diaspora à la suite duquel l’AfAS nouvelle version fut lancée et un nouveau comité directeur fut élu. Depuis, l’AfAS s’est mise à pied d’œuvre à travers ses différents comités et s’est lancée dans d’ambitieux programmes tant pour les astronomes professionnels qu’amateurs. De plus amples détails se trouvent sur le site de l’association.
Notons qu’un important développement a eu lieu en avril dernier lorsque l’AfAS est devenue un consortium englobant un certain nombre d’autres associations astronomiques continentales dont l’ African Planetariums Association (APA) et l’African Science Stars, toutes ayant aussi leurs sièges en Afrique du Sud, mais chapeautées toujours par l’AfAS.
Visions et objectifs principaux de l’AfAS
L’ambition de l’AfAS est de créer une communauté astronomique compétitive à l’échelle mondiale en Afrique. Elle se veut aussi être au service de la communauté amateur et du grand public.
Ses missions principales peuvent être déclinées comme suit:
– Être la voix de l’astronomie en Afrique
– Contribuer à relever les défis auxquels l’Afrique est confrontée à travers la promotion et l’avancement de l’astronomie.

Fig 2: Activités scolaires de diffusion de la culture astronomique à l’aide de planétarium portables au Kenya

Fig 3: Activités scolaires de diffusion de la culture astronomique à l’aide de planétarium portables en Algérie
– L’inclusion de l’astronomie dans le domaine du développement social et économique.
– L’utilisation de l’astronomie pour attirer les jeunes africains vers des carrières en sciences, technologie, ingénierie et mathématiques
– L’organisation de conférences thématiques et des campagnes d’observation lors d’événements astronomiques et des domaines connexes.
– Sauvegarder les sites astronomiques en Afrique et les connaissances autochtones du ciel.
Capitaliser sur les grands instruments Africains
L’AfAS, comme but stratégique, voudrait tirer parti de l’avantage géographique naturel de l’Afrique et capitaliser sur l’existence de grands instruments de classe mondiale sur le continent. Mentionnons les rapidement: Il y a notamment le telescope optique SALT (South African Large Telescope) sur le plateau du Sutherland (Afrique du Sud), qui est considéré comme le plus grand télescope optique d’astronomie optique au monde, télescope de type Hobby–Eberly avec un miroir principal de 11 m. Puis vient le radio-télescope MeerKAT dans le semi désert du Karoo toujours en Afrique du Sud et qui préfigure le futur SKA (Square Kilometer Array), un des plus grands projets de radioastronomie dans le Monde. Concluons la liste en mentionnant les télescopes du projet HESS pour l’astronomie gamma en Namibie.

Fig 4: Photo prise par le radiotélescope MeerKAT offrant en radio la vue la plus claire à ce jour du centre de notre Galaxie situé à quelque 25.000 années-lumière de la Terre.
Ces différents projets sont à même de jouer le rôle de locomotive pour l’astronomie professionnelle africaine et constituer une puissante source d’inspiration pour les astronomes amateurs et les jeunes scientifiques du continent en général. Il est un fait que jusqu’à présent, tout ces atouts n’ont pas suffisamment profité du talent humain africain et c’est ce qui devrait changer.
En Conclusion
A bien des égards, l’astronomie est une science africaine avec une riche tradition populaire à travers tout le continent. Il est temps de la valoriser, la faire fructifier, ainsi que de la mettre au diapason de l’astronomie mondiale.
C’était là quelques perspectives sur les premiers pas de la Société Astronomique Africaine. Nous invitons tous les individus et parties intéressés et à même de contribuer, à se joindre à nous pour faire progresser l’astronomie sur notre continent.
Jamal Mimouni – Président, AfAS



















