
par Sylvain Bouley | Jan 9, 2023 | Non classé
| 02/02/2023 |
Rapprochement entre la Lune et M 35 |
| 03/02/2023 |
Rapprochement entre la Lune et Pollux |
| 04/02/2023 |
Lune à l’apogée (distance géoc. = 406476 km) |
| 05/02/2023 |
Pleine Lune |
| 06/02/2023 |
Rapprochement entre la Lune et Régulus

|
| 13/02/2023 |
Dernier Quarter de la Lune |
| 18/02/2023 |
Rapprochement entre la Lune et Mercure avant le lever du Soleil

|
| 19/02/2023 |
Lune au périgée (distance géoc. = 358267 km) |
| 20/02/2023 |
Nouvelle Lune |
| 22/02/2023 |
Rapprochement entre la Lune, Jupiter et Vénus après le coucher du Soleil

|
| 27/02/2023 |
Premier Quartier de Lune |
| 28/02/2023 |
Rapprochement entre la Lune et Mars en première partie de nuit

|
| 28/02/2023 |
Rapprochement serré entre Vénus et Jupiter après le coucher de Soleil |

par Sylvain Bouley | Oct 13, 2022 | Actualités
Selon des simulations numériques d’impacts géants, il serait très difficile de former de gros satellites autour de planètes rocheuses de masse supérieure à 6 masses terrestres.


Si l’on met de côté le cas un peu particulier du couple Pluton-Charon, la planète du Système solaire possédant le plus gros satellite par rapport à sa propre masse est la Terre. La Lune représente en effet plus de 1 % de la masse terrestre. Cette configuration serait le résultat d’un impact géant survenu il y a environ 4,47 milliards d’années (Ga) entre une planète, la proto-Terre, un peu plus petite que la Terre elle-même, et un objet de la taille de Mars, Théia. Cet impact aurait détruit Théia et excavé une partie du manteau terrestre. Et c’est à partir de ce matériau rassemblé en un disque de gaz et de débris que la Lune se serait formée. Selon les modèles actuels d’évolution du Système solaire, les impacts géants auraient été inévitables, et même communs, dans la jeunesse de celui-ci. Au point que l’on se demande pourquoi Vénus ne possède pas, elle aussi, un gros satellite1. Une autre question brûle les lèvres : qu’en est-il des autres systèmes planétaires ? De nombreuses exoplanètes de taille comparable à la Terre (exo-Terres) ou un peu plus grosses (super-Terres) ont été recensées. Celles-ci possèdent-elles, dans leur majorité, de grosses exo-lunes ? Une équipe de chercheurs dirigée par Miki Nakajima, de l’université de Rochester, s’est penchée sur cette question à l’aide de simulations numériques d’impacts géants2. Ces chercheurs notent tout d’abord qu’une étude approfondie réalisée sur une soixantaine de super-Terres répertoriées dans le catalogue de la mission Kepler n’a mis en évidence aucune exo-lune autour de ces exoplanètes. Détecter une exo-lune n’est évidemment pas une mince affaire, et ce résultat négatif ne signifie pas que les super-Terres sont systématiquement dépourvues de satellite. Mais il se pourrait aussi qu’il traduise une tendance bien réelle. C’est en tout cas ce que suggèrent les simulations numériques de Miki Nakajima et de ses collègues (fig. 1). Selon ces calculs, la formation d’un gros satellite à la suite d’un impact géant ne pourrait pas se produire pour des super-Terres rocheuses de 6 masses terrestres ou plus (fig. 2), ce qui correspond à des planètes d’au moins 1,6 rayon terrestre. Pour des super-Terres composées de glace, la masse seuil tombe à une masse terrestre, soit une planète d’environ 1,3 rayon terrestre. Ce résultat s’explique par la quantité d’énergie libérée pendant l’impact, qui est d’autant plus élevée que la masse totale du système (proto-planète plus impacteur) est grande. Or, plus cette énergie est élevée, plus la fraction de matériau à l’état de vapeur dans le disque de débris est importante. Un embryon de satellite de 100 m à 100 km se formant dans un tel disque est soumis à d’intenses forces de frottement qui le poussent à migrer vers la planète mère. Son destin est alors inéluctable : il va, à brève échéance, franchir la limite de Roche et se disloquer. Difficile, dans ces conditions, de former un gros satellite.
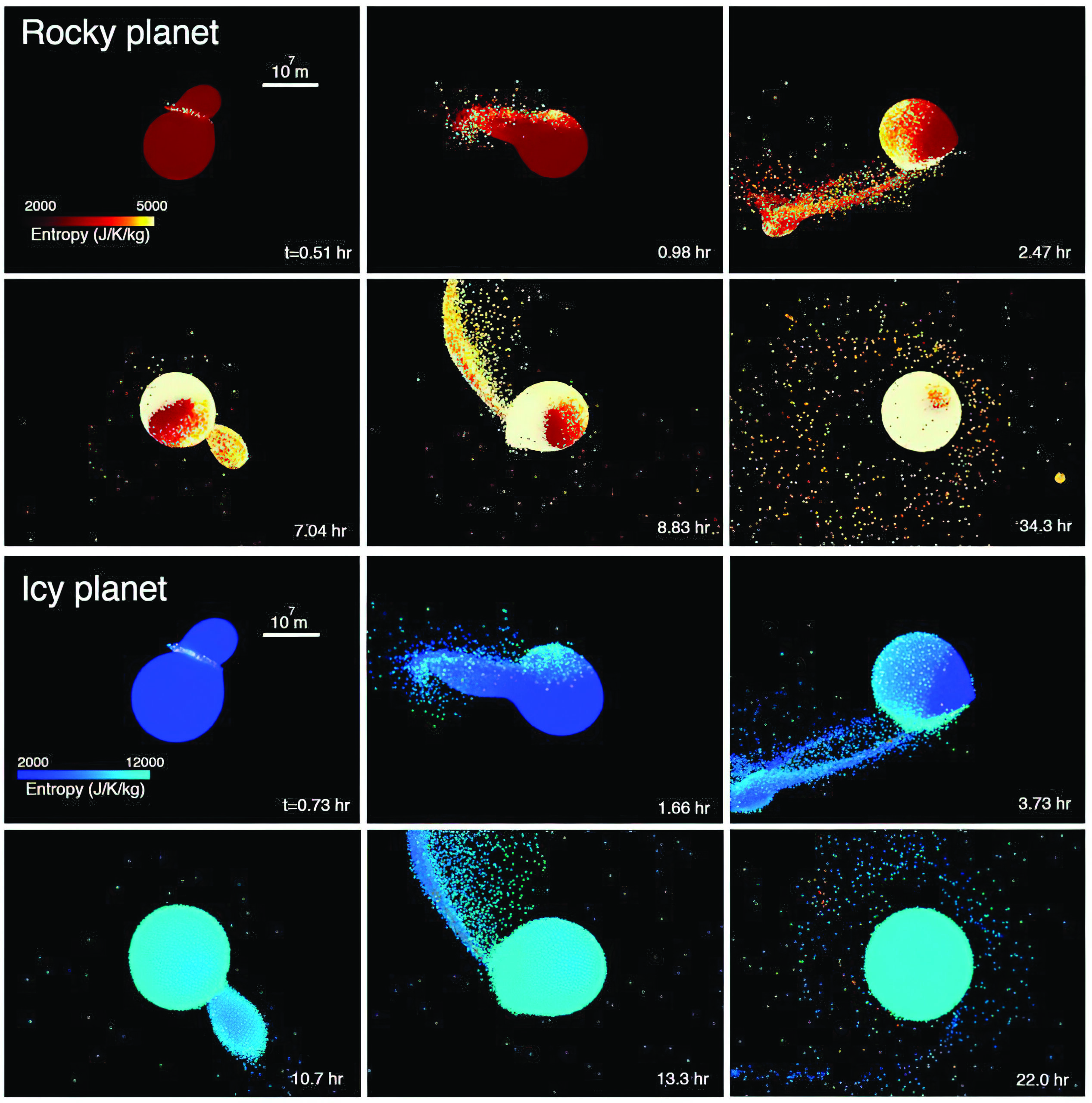
1. Deux simulations numériques pour des planètes d’une masse terrestre, en haut (Rocky planet), pour une planète rocheuse, et en bas (Icy planet) pour une planète de glace. Dans le premier cas, il se forme bien un satellite, mais pas dans le second. Pour les planètes rocheuses, la masse seuil au-dessus de laquelle la formation d’un satellite est entravée est de 6 masses terrestres. (Nakajima et al., 2022)
Si ces simulations reflètent la réalité, la chasse aux exo-lunes autour de super-Terres pourrait s’annoncer plus compliquée que prévu. Elle devra en effet se focaliser sur des planètes de taille comparable à celle de la Terre, ce qui requiert des moyens d’observation plus puissants que pour une recherche similaire autour de super-Terres. Ce résultat compromet aussi quelque peu l’habitabilité des super-Terres. La présence de la Lune permet en effet de maintenir l’inclinaison de l’axe de rotation de la Terre dans une gamme de valeurs relativement étroite. Notre planète peut ainsi se prémunir de variations climatiques trop extrêmes ou fréquentes, donnant à la vie le temps nécessaire pour évoluer vers des formes complexes.
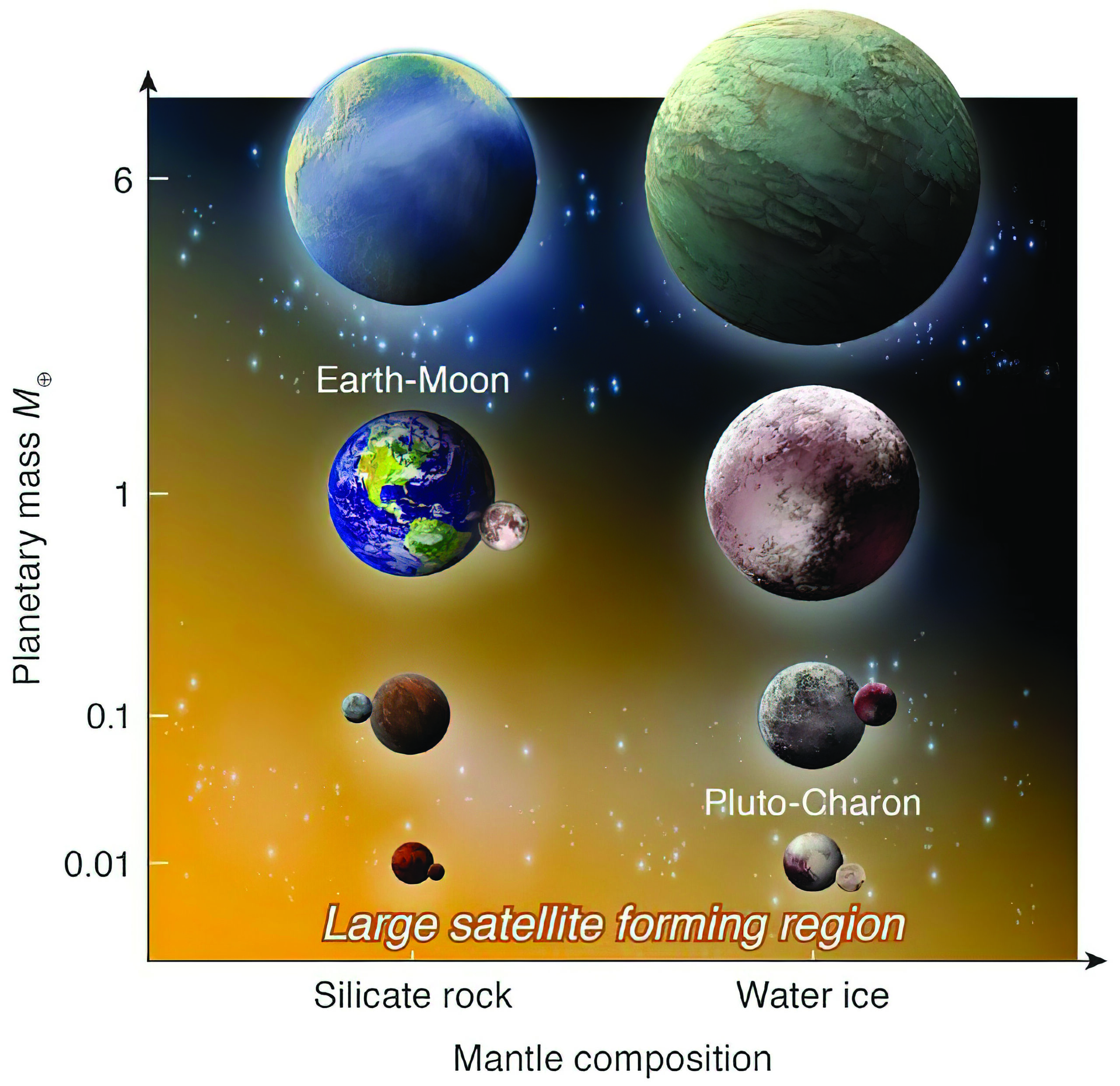
2. Selon les simulations numériques de Miki Nakajima, la formation de gros satellites suite à un impact géant n’est sans doute pas possible pour les super-Terres trop massives. Le seuil se situe autour de 6 masses terrestres pour les planètes rocheuses (à gauche), et une masse terrestre pour les planètes de glace (à droite). (© Nakajima et al., 2022)
Frédéric Deschamps, IESAS, Taipei, Taïwan
Notes
- Cette question n’a pour le moment pas de réponse. Une hypothèse est que Vénus aurait subi deux impacts. Le premier aurait bien créé un satellite, mais le second aurait modifié la rotation de Vénus de telle façon que, sous l’effet des forces de marée, ce satellite aurait migré vers Vénus au lieu de s’en éloigner, et se serait disloqué en franchissant la limite de Roche. Cette explication a le mérite d’expliquer la vitesse de rotation faible et rétrograde de Vénus. Mais il est aussi possible que Vénus n’ait pas subi d’impact géant.
- Nakajima M. et al., « Large planets may not form fractionally large moons », Nature Communications, 13:568, 2022. doi : 10.1038/s41467-022-28063-8.

par Sylvain Bouley | Oct 13, 2022 | Zoom Sur
Année 2007, les astronomes détectent un pulsar à l’emplacement de ce qu’ils croyaient être depuis des années une variable cataclysmique : l’astre qu’ils croyaient être une étoile naine blanche d’une dizaine de milliers de kilomètres de diamètre (comparable à la Terre) et d’une masse de quelques dixièmes de la masse du Soleil (100 000 fois la Terre) s’avère être en réalité une étoile à neutrons*, c’est-à-dire un résidu d’étoile massive de seulement 20 km de diamètre et un milliard de fois plus dense qu’une naine blanche avec une masse d’environ 1,5 fois la masse du Soleil. Comment a-t-on pu faire une telle méprise ? C’est ce que nous allons essayer de voir dans le reste de cet article.

Un * renvoie au glossaire en fin d’article.
L’ESSENTIEL
Un pulsar est une étoile à neutrons magnétisée tournant très vite, que l’on peut observer en ondes radio, ou X ou gamma. Un pulsar émet beaucoup d’énergie, ce qui ralentit sa rotation au point qu’après quelques millions d’années, il s’éteint. Il reste une étoile à neutrons presque inerte. Cependant, d’anciens pulsars formant un système double avec une étoile peuvent accréter de la matière de leur compagnon, ils gagnent alors de la vitesse de rotation et se transforment à nouveau en pulsar. Le vent émis par le pulsar réactivé va progressivement faire disparaître le compagnon stellaire ayant permis son réallumage. Des observations très différentes du même objet, appelé J1023, menées en 2000, 2001, 2004 et 2007 ont été interprétées récemment comme provenant d’un système de deux étoiles subissant cette transformation. L’article, qui décrit cette transformation d’un système binaire en un pulsar milliseconde, tel qu’il est observé entre 2007 et 2013, est rédigé par un des coauteurs d’une étude de J1023 publiée cette année. Mentionnons que ce jeune chercheur a obtenu son doctorat en 2017, et qu’il a reçu le prix de la meilleure thèse de l’Union astronomique internationale, dans la thématique « phénomènes de haute énergie et physique fondamentale ».

1. Schéma représentant un pulsar. L’étoile à neutrons est en rotation autour de l’axe vertical vert. Les lignes blanches représentent le champ magnétique de l’étoile. Le cône bleu s’échappant des pôles magnétiques représente le faisceau d’ondes radio émis. Un observateur voit passer le faisceau à chaque rotation de l’étoile sous la forme d’une impulsion radio revenant avec une très grande régularité. (Mysid, CC BY-SA 3.0)
Genèse d’un pulsar
Un pulsar est constitué d’une étoile à neutrons qui elle-même est un résidu d’étoile massive. Par massive, on entend une étoile faisant plus de 8 fois la masse du Soleil. Les étoiles moins massives, et en particulier le Soleil, ont pour résidu une naine blanche qui, comme mentionné dans le texte, est à la fois beaucoup plus volumineuse et moins massive qu’une étoile à neutrons. Toutes les étoiles en activité résultent de l’équilibre entre la pression générée par la fusion nucléaire en leur cœur et la gravité qui tend à les faire s’effondrer sous leur propre poids. Une étoile « meurt » lorsque son combustible nucléaire est épuisé et que les réactions nucléaires s’arrêtent, menant à l’effondrement du cœur tandis qu’une grande partie de l’enveloppe de l’étoile est éjectée dans l’espace dans un dernier souffle. Dans le cas des étoiles massives, ce dernier souffle est particulièrement impressionnant : il s’agit d’une supernova dont la luminosité peut excéder la luminosité combinée de toutes les autres étoiles de sa galaxie hôte. Dans le cas d’une étoile de moins de 8 masses solaires, le résidu fait moins que la masse limite, dite de Chandrasekhar, laquelle vaut 1,4 masse solaire. Avec une telle masse, la pression de dégénérescence des électrons, c’est-à-dire la pression due au fait que deux électrons ne peuvent occuper le même état (la même position et la même vitesse essentiellement), suffit à stopper l’effondrement et l’on obtient une naine blanche. Dans le cas d’étoiles dont le résidu est plus massif, la pression de dégénérescence des électrons ne suffit pas et l’effondrement continue. Sous l’effet de la pression, les électrons se mêlent aux protons pour former des neutrons (ainsi que des neutrinos). Si c’est finalement la pression de dégénérescence des neutrons qui arrête l’effondrement, une étoile à neutrons se forme. Si cela ne suffit pas, alors il semble que rien ne puisse enrayer l’effondrement et un trou noir se forme. Avoir une étoile à neutrons ne signifie cependant pas nécessairement avoir un pulsar. Pour cela, on sait qu’une condition nécessaire est que celle-ci soit dotée d’une magnétosphère capable de produire des champs électriques très intenses, au moins de l’ordre de 1012 volts/mètre, capables d’exciter le plasma piégé dans la magnétosphère à de très hautes énergies ! Cela est possible si l’étoile tourne suffisamment vite sur elle-même, en pratique de 1,5 milliseconde à 8,5 secondes par tour, et si son champ magnétique est particulièrement intense, de plus de 10 000 à 1010 teslas.
Rebaptisé pour l’occasion PSR J1023+0038, l’astre se situe comme son nom l’indique à 10 h et 23 min en ascension droite et à 38 minutes en déclinaison dans le référentiel appelé « J2000 ». Le préfixe « PSR » est simplement l’abréviation de pulsar*. Le pulsar J1023 – les intimes ne s’embarrassent pas souvent de la déclinaison, laquelle est un peu comme le nom de famille de l’objet – n’avait pas été détecté plus tôt pour au moins une bonne raison : il n’était pas là ! Ou du moins, il était trop faible pour être détecté.
Lorsque les astronomes observent dans cette direction entre mai 2000 et décembre 2001 [1], ce qu’ils voient est une source radio continue, et en lumière visible un objet de magnitude 17,5 dont le spectre est très bleu. Surtout, le spectre montre des raies d’émission dédoublées ainsi qu’un scintillement rapide de l’intensité lumineuse, deux éléments caractéristiques des disques d’accrétion spiralant autour des naines blanches dites « variables cataclysmiques ». Jetant un coup d’œil à leurs archives, les astronomes remarquent que le flux radio observé était absent quelques années plus tôt, montrant que cette source varie beaucoup dans le temps. Les astronomes concluent qu’il est urgent d’en apprendre plus, et d’autres observations sont prévues.
Quelques années plus tard, en mars 2004, on assiste à un nouveau développement alors que J1023 est réobservé [3,4] : le spectre bleu, les raies d’émission, le scintillement… tout a disparu. À la place, une simple étoile de type G, comme le Soleil, à cela près que son intensité lumineuse varie mystérieusement avec une période de 4,75 heures.
Nous revoilà en 2007. Compte tenu de tout ce qui avait déjà été observé à l’emplacement de J1023, qu’est-ce qui a fait soudainement dire aux astronomes qu’un pulsar se nichait là ? Pour cela, il faut comprendre ce dont il s’agit exactement. Comme nous l’avons déjà mentionné, un pulsar est une étoile à neutrons, l’objet connu le plus compact qui ne s’effondre pas en trou noir (voir encadré). Dans certains cas au moins, ces objets sont dotés des champs magnétiques les plus extrêmes que nous connaissions, allant de 10 000 teslas à quelques milliards de teslas. Pour comparaison, le champ magnétique terrestre fait moins de 0,0001 tesla et les meilleures expériences en laboratoire ne parviennent à produire que des champs de 1 000 teslas, et encore, pendant une petite fraction de seconde, alors que dans les pulsars le champ est permanent ! Le résultat, c’est que le plasma piégé dans ce que l’on appelle la magnétosphère* du pulsar – la zone où l’influence du champ magnétique domine le plasma qui s’y trouve – produit toutes sortes de rayonnements. Les plus faciles à détecter, et de loin, sont les émissions radio. Surtout, cette émission vue par les radiotélescopes terrestres est pulsée, constituée d’un signal radio bref – un « bip » – répété avec une régularité non pas de métronome, mais d’horloge atomique : dans les meilleurs cas, il est possible de prédire le prochain bip avec une précision de 100 nanosecondes (un dix-millionième de seconde). Cela se comprend très bien si l’on considère que le signal fait partie d’un faisceau étroit produit en continu dans la magnétosphère et que l’étoile tourne sur elle-même, entraînant par là sa magnétosphère et le faisceau avec elle. L’étoile à neutrons se comporte alors comme un phare radio cosmique ! L’observateur, lui, voit passer le faisceau toutes les quelques millisecondes jusqu’à quelques secondes suivant la période de rotation de l’étoile. Pour que chaque impulsion soit aussi brève, il faut nécessairement que la zone d’émission, et donc l’étoile, soit particulièrement petite, ce qui élimine tous les types d’étoiles connus sauf les étoiles à neutrons. En résumé, lorsqu’un radiotélescope détecte un signal bref et périodique, si ce n’est pas la clôture électrique gardant les vaches dans un champ voisin (les radiotélescopes sont très sensibles au moindre signal électromagnétique d’origine humaine), alors il s’agit très certainement d’un pulsar, et c’est ce qui a été observé en 2007 (fig. 1) !
Mesurer le déplacement d’une horloge en écoutant ses tic-tac
Une conséquence particulièrement utile de la régularité d’un pulsar est le fait de pouvoir l’utiliser comme une horloge que l’on aurait posée à cet endroit précis de l’espace et qui nous transmettrait à chaque battement l’heure qu’il est, c’est-à-dire ici le nombre de rotations effectuées depuis que l’observateur a commencé à les compter. Et cela bien sûr sans que personne n’ait eu à faire un trajet de centaines ou de milliers d’années-lumière pour aller l’installer ! La nature fait bien les choses… mais, en fait, à quoi cela sert-il d’avoir des horloges éparpillées dans la Galaxie ? Très simplement, si quoi que ce soit vient perturber l’horloge, le tic-tac si régulier se met à battre la chamade, ou alors à ralentir. C’est exactement ce qui se passe chez J1023 en 2007, et ce d’une façon bien caractéristique que l’on observe à chaque fois qu’un pulsar est dans un système binaire avec une autre étoile. Ici, rien de bien surprenant car, après tout, on avait déjà repéré qu’il y avait là une étoile normale. La signature que l’on observe dans le chronométrage des impulsions du pulsar nous donne aussi plusieurs informations précieuses, dont la période orbitale du pulsar avec son compagnon. En effet, comme les deux objets sont de masses assez similaires, tous deux décrivent des orbites assez amples, contrairement au Soleil, dont on a parfois tendance à penser qu’il est immobile au milieu du Système solaire : cet apparent immobilisme n’est qu’une illusion due à sa masse immensément plus grande que celle des planètes.
Dans le cas de J1023, le pulsar se déplace de centaines de milliers de kilomètres autour du barycentre commun aux deux étoiles, ce qui est suffisant pour retarder l’arrivée du tic d’environ 1 seconde au radiotélescope quand le pulsar s’éloigne de la Terre – une fois l’effet de projection de l’orbite le long de la ligne de visée pris en compte – et avancer le tac de façon similaire lorsque le pulsar se rapproche de la Terre. Cet effet, aussi appelé retard de Rœmer (fig. 2), est le principal effet qui permette de déduire la période orbitale qui n’est autre que… 4,75 heures : la même que la période de la variation de l’intensité lumineuse de l’étoile compagnon détectée en 2004 ! Bon, les astronomes savaient déjà que cette variation était liée à l’orbite de l’étoile compagnon avec ce qu’ils pensaient à l’époque être une naine blanche, car cela est en fait un phénomène relativement commun. Néanmoins, l’astronomie est un peu un travail de détective : l’astronome ne dispose que de quelques indices, qu’il faut croiser, valider et confirmer sans cesse pour déterminer quelle est, au final, l’hypothèse la plus probable. Par ailleurs, les mesures effectuées par la méthode du chronométrage de pulsar sont généralement de loin les plus précises, pour les raisons expliquées plus haut, même si elles sont incapables dans le cas présent de donner à elles seules toutes les informations sur l’orbite [1].
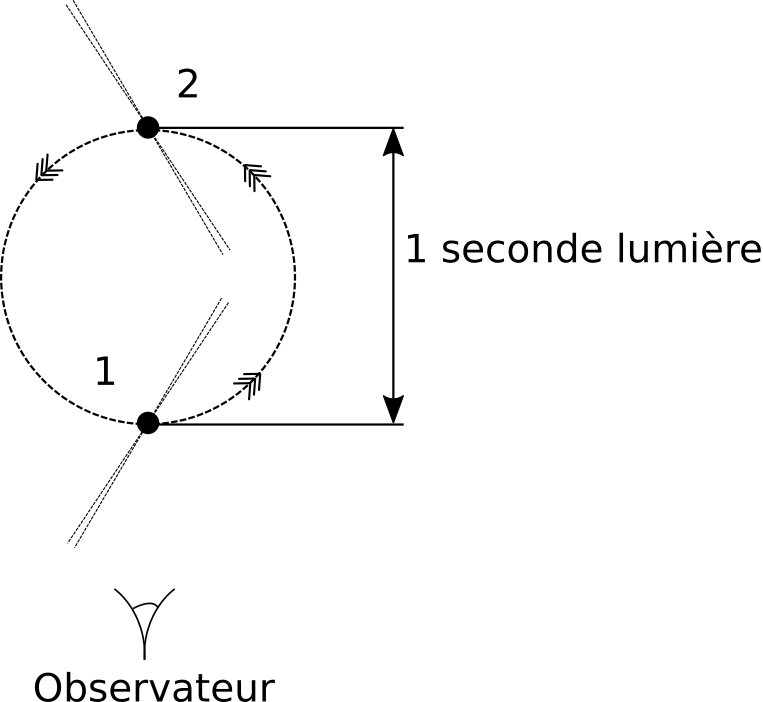
2. Retard de Rœmer. On voit ici le pulsar à deux positions différentes sur son orbite, numérotées 1 et 2. Lorsque le pulsar est à la position 2, les impulsions radio qu’il émet mettent environ 1 seconde de plus pour parvenir à l’observateur que lorsqu’il se trouve en position 1, ce qui se traduit par un retard égal du temps d’arrivée au télescope de l’impulsion comparé avec ce que l’on attendrait d’un pulsar immobile. (Guillaume Voisin, CC BY-SA 4.0)
L’aspect du système binaire*
Le lecteur attentif aura peut-être noté qu’à aucun moment, je n’ai parlé d’image du système J1023, mais seulement d’intensité, de spectre, de signal ou encore de bip, de tic et de tac. Il est en fait impossible de simplement prendre une photographie où l’on verrait d’un côté le pulsar, et de l’autre le compagnon. D’abord parce que le pulsar, comme la plupart de ses congénères, n’apparaît pas en lumière visible, ensuite parce que la distance entre les deux étoiles est de seulement 4 secondes-lumière (environ 1 million de kilomètres), mais se situe à environ 4 300 années-lumière (environ 10 000 milliards de kilomètres). Discerner les deux objets reviendrait à pouvoir discerner les rovers lunaires laissés par les missions Apollo sur la Lune, ce qui est impossible même avec les meilleurs instruments. En revanche, nous voyons très bien les variations d’intensité, et cela peut nous apprendre beaucoup à condition d’avoir un peu d’imagination.
Supposons que nous puissions nous approcher à dix ou vingt millions de kilomètres sans être instantanément irradiés et bouillis par les rayonnements des deux étoiles, que verrions-nous ? L’étoile compagnon nous apparaîtrait comme happée vers un astre invisible, complètement étirée dans la direction du rayon de son orbite, la face intérieure comme aspirée dans un entonnoir. Ce que nous verrions est l’effet de marée gravitationnelle : la face intérieure du compagnon est plus proche du pulsar et donc plus attirée par ce dernier que la face extérieure, ce qui résulte en un étirement. Nous connaissons aussi ce phénomène sur Terre, quand la Lune attire plus les océans du côté de la Terre qui lui fait face que du côté opposé, provoquant un déplacement des masses d’eau. La Terre entière et la Lune se déforment aussi mutuellement, mais de façon imperceptible à l’échelle humaine. À l’échelle du compagnon, la combinaison des attractions gravitationnelles des deux étoiles et de la force centrifuge due à la grande vitesse orbitale crée ce que les astronomes appellent le lobe de Roche du compagnon : un volume en forme de goutte d’eau, pointant vers le pulsar, à l’intérieur duquel la gravité du compagnon domine les deux autres forces. Dans le cas présent, le compagnon remplit pratiquement ce lobe, ce qui lui donne sa forme. Observé de la Terre, cela se voit dans la courbe d’intensité reçue : lorsque nous voyons le « flanc » du compagnon, celui-ci apparaît plus lumineux que lorsque nous le voyons suivant sa section la plus étroite, simplement parce que la surface rayonnant en direction de la Terre varie au cours de l’orbite. On appelle cela la modulation ellipsoïdale, à cause de la forme approximative de l’étoile étirée. Comme l’étoile a deux flancs, la modulation ellipsoïdale de l’intensité présente donc deux maxima par orbite.
Le pulsar, lui, n’est pas visible, même à cette distance : il est minuscule en comparaison de son compagnon, qui fait plusieurs centaines de milliers de kilomètres, et le voir reviendrait à être capable de discerner un stade de football à la surface de la Lune. De toute façon, la très faible quantité de lumière visible qu’il émet serait engloutie dans le déluge provenant du compagnon, rendant le contraste difficile à percevoir. Tournons un peu autour, la face externe du compagnon est plus arrondie que la face interne, et surtout elle est beaucoup moins lumineuse, c’est littéralement la nuit et le jour. En effet, le compagnon montre toujours la même face au pulsar, il tourne sur lui-même à la même vitesse qu’il parcourt son orbite, comme la Lune autour de la Terre. Ce faisant, il absorbe une partie des radiations et des particules émises par le pulsar, ce que l’on appelle le vent. Bien que n’émettant pas en lumière visible, le pulsar rayonne en effet une remarquable quantité d’énergie à chaque instant, jusqu’à l’équivalent de 100 Soleils dans le cas de J1023 ! Même en absorbant seulement 10 % de cette énergie, la face jour du compagnon est surchauffée et brille d’autant plus fort. C’est là l’origine de la modulation jour-nuit, la plus importante modulation de l’intensité reçue par les télescopes observant J1023 : lorsque la face jour du compagnon fait face à la Terre, l’intensité est au maximum, alors qu’une demi-période plus tard, nous voyons la face nuit et l’intensité baisse à son minimum (fig. 3).
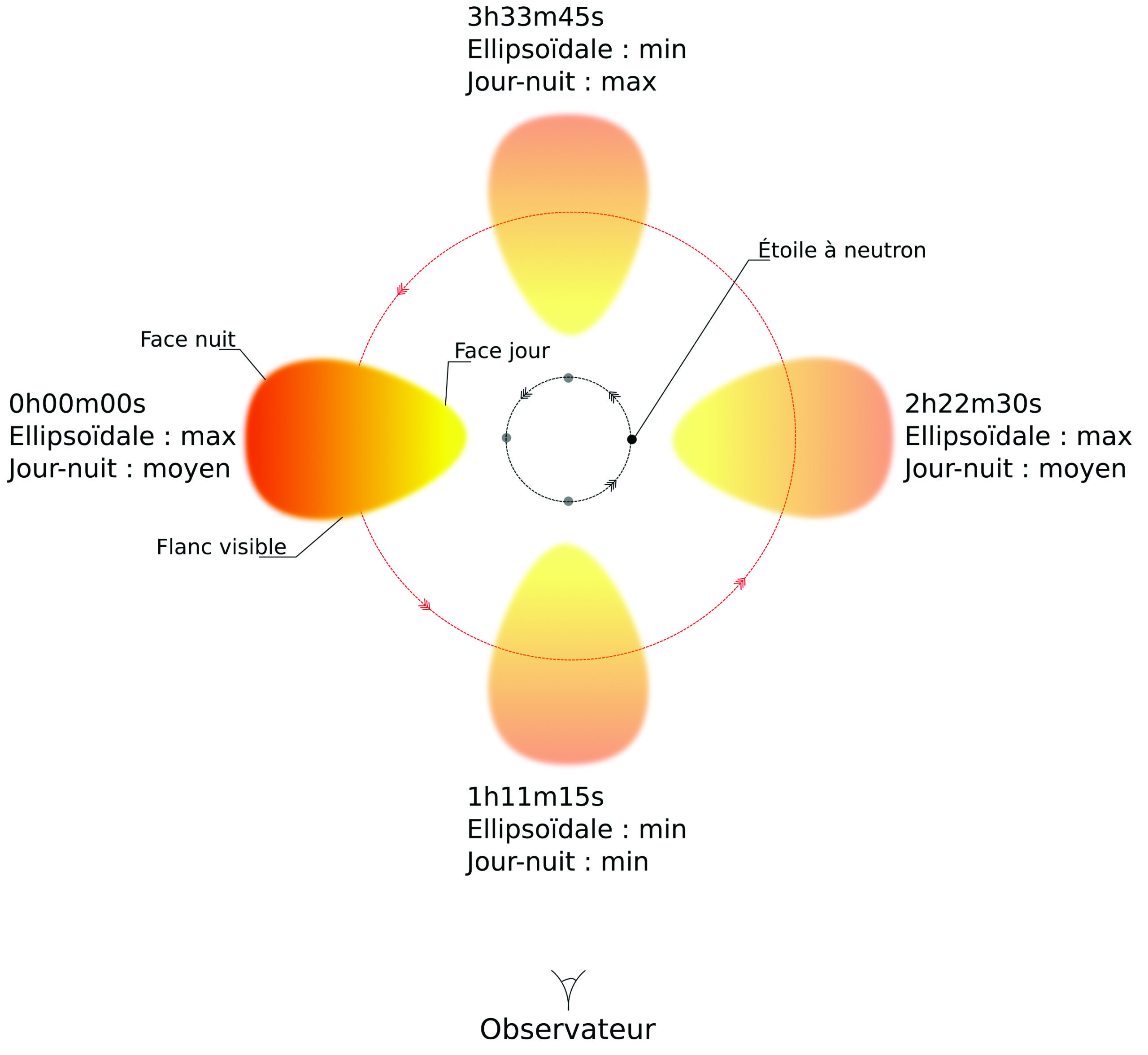
3. Une orbite complète de J1023, 4h 45min, avec les différentes étapes des modulations ellipsoïdale et jour-nuit. (Guillaume Voisin, CC BY-SA 4.0)
Les veuves noires à dos rouge
Par ailleurs, l’endroit n’est pas très propre, il y a du gaz qui traîne un peu partout. Le coupable semble tout désigné, car le gaz se trouve essentiellement autour du compagnon. On ne le voit pas directement en lumière visible, le gaz est trop ténu pour cela. En revanche, il est capable de bloquer le faisceau d’ondes radio émis par le pulsar, provoquant ainsi des éclipses radio à chaque fois que le compagnon passe entre le pulsar et la Terre, bien que le compagnon lui-même ne soit pas sur le chemin du faisceau. Mais ce serait aller un peu vite que de juger le compagnon comme étant l’unique responsable de ce bazar. Le pauvre est en fait plutôt la victime de la violence du vent du pulsar et des terribles forces de marée qui s’exercent sur lui. Résultat, le compagnon s’évapore petit à petit, perdant peut-être jusqu’à un cent-milliardième de sa masse par an, presque rien, mais quand même environ 1019 kg, soit la masse d’un planétoïde de quelques centaines de kilomètres tous les ans.
Dans cet état, J1023 est un représentant d’une classe de pulsars que l’on appelle les « araignées ». Ce surnom n’est pas vraiment lié à la capacité du pulsar à tisser une toile ni à son nombre de pattes, mais plutôt à sa tendance à dévorer, ou plutôt à évaporer, son compagnon. Plus précisément, les astronomes ont classé J1023 dans l’espèce des veuves noires à dos rouge (fig. 4). Cette espèce d’araignée originaire d’Australie a en effet la particularité que la femelle, beaucoup plus grosse que le mâle, dévore occasionnellement son compagnon après la copulation. C’est bien ce que l’on retrouve chez J1023 et les autres systèmes similaires : madame pulsar est jusqu’à plus de dix fois plus massive que son compagnon, bien que beaucoup plus petite, due à sa haute densité. En revanche il n’est pas clair que l’évaporation aille toujours jusqu’au bout et il se pourrait que le compagnon survive au moins dans certains cas. Déterminer le taux d’évaporation par l’observation est en effet particulièrement ardu, mais prévoir comment ce taux va évoluer dans le temps l’est tout autant et ce point est un sujet d’intenses débats dans la communauté scientifique. Il ne s’agit pas seulement pour les scientifiques de savoir à quelle sauce le compagnon va être mangé par son étoile à neutrons, mais aussi de lever le voile sur l’existence des pulsars milliseconde isolés (voir encadré).

4. Une femelle veuve noire à dos rouge. Le compagnon mâle est trois fois plus petit et se trouve souvent dévoré après l’accouplement. Chez les pulsars, le ratio, en termes de masse, est typiquement de trois à dix. (Toby Hudson, CC BY-SA 3.0)
Des étoiles géantes rouges font du recyclage
Les pulsars milliseconde sont les pulsars les plus rapides connus. Comme leur nom l’indique, leur période de rotation sur eux-mêmes est de l’ordre de quelques millisecondes. Il se trouve que J1023 est un pulsar milliseconde, avec une période d’environ 1,7 milliseconde. Sans entrer dans les détails, on ne voit pas comment un pulsar peut être formé avec une rotation aussi rapide (voir encadré). La plupart des pulsars « jeunes », dont l’âge est estimé de quelques dizaines à quelques centaines de milliers d’années, ne tournent d’ailleurs pas plus vite que quelques centièmes de seconde par tour, et le plus souvent en 0,1 ou 1 seconde par tour. L’estimation de l’âge des pulsars milliseconde est quant à elle beaucoup plus grande, se chiffrant potentiellement en milliards d’années. Se pourrait-il alors que les pulsars accélèrent avec le temps ? Pas vraiment, c’est même plutôt le contraire : la mesure fine des temps d’arrivée des impulsions radio, la technique dite du chronométrage, indique en effet que les pulsars ralentissent tous. C’est d’ailleurs ce à quoi l’on s’attend à partir de simples arguments d’ingénierie électromagnétique : imaginez, un pulsar n’est en première approche qu’un gros aimant en rotation sur lui-même. C’est-à-dire ce que l’on trouve dans n’importe quel moteur ou dynamo électrique. Sa rotation sur lui-même produit de l’énergie électromagnétique, énergie qui provient de la rotation. On en arrive à la très générale loi de Lenz de l’électromagnétisme, qui prédit que tout effet du champ électromagnétique s’oppose à sa cause.
Ainsi, à force de ralentir, les pulsars en arrivent à ne plus être capables de produire de rayonnements observables et deviennent de simples étoiles à neutrons invisibles à nos télescopes. Cela se produit assez vite, tant et si bien qu’il est très improbable d’observer des pulsars de plus d’un milliard d’années, rendant l’existence des pulsars milliseconde encore plus mystérieuse.
Alors, comment les pulsars milliseconde se forment-ils ? Ils ont besoin que quelque chose d’extérieur vienne les accélérer, par exemple un compagnon ! Lorsqu’une étoile massive explose en supernova et forme un pulsar, son éventuelle compagne* reste en orbite avec le pulsar nouvellement né. Si cette étoile est petite ou moyenne, comme le Soleil, elle pourra vivre pendant des milliards d’années avant de s’éteindre à son tour, laissant au pulsar le temps de ralentir jusqu’à l’extinction. Vers la fin de sa vie, une étoile analogue au Soleil gonfle dans de très grandes proportions en formant une géante rouge et son rayon peut être aisément multiplié par cent. Dans le cas du Soleil, par exemple, on pense que la Terre sera très proche, voire à l’intérieur de la surface de l’étoile, ce qui sent un peu le roussi pour la planète.
Mais, si au lieu de la Terre, est présente une étoile à neutrons, l’histoire est bien différente : c’est la géante rouge qui risque d’avoir quelques ennuis ! Le gaz de la géante, attiré et étiré par les forces gravitationnelles de l’étoile à neutrons, sort de la zone d’attraction du compagnon, son lobe de Roche, et se met à spiraler autour de celle-ci, formant ce que l’on appelle un disque d’accrétion. Sous l’effet de la friction au sein du gaz, celui-ci ralentit et perd de l’altitude jusqu’à s’écraser, un peu comme les satellites de basse altitude s’écrasent sur Terre à cause de la friction de l’atmosphère lorsqu’ils n’ont plus de carburant pour les rehausser régulièrement. Il résulte qu’une énorme quantité de matière, de l’ordre de plusieurs dixièmes de la masse du Soleil, s’écrase à très grande vitesse sur l’étoile à neutrons, non pas verticalement, mais plutôt tangentiellement à la surface, un peu comme de l’eau entraînant une roue à aubes. Si lorsqu’un satellite s’écrase sur Terre, cette dernière n’en est pas plus affectée qu’un gros éléphant par une piqûre de petit moustique, ce déluge de gaz est en principe suffisant pour accélérer la rotation de l’étoile à neutrons d’une période de plusieurs secondes jusqu’à une poignée de millisecondes une fois l’accrétion terminée. Reste à savoir si une fois ce traitement de choc subi l’étoile conserve sa capacité à être un pulsar. En effet, l’évolution de son champ magnétique pose notamment question, et sans champ magnétique, point de magnétosphère et point de rayonnement.
Ce scénario, qui pourrait expliquer l’existence des pulsars milliseconde comme J1023, a été imaginé très tôt après la découverte du premier pulsar milliseconde en 1982 [5,6], et a depuis été surnommé le mécanisme de recyclage des pulsars, car ceux-ci échappent à la mort par ralentissement grâce à la réaccélération (fig. 5). Il restait à prouver que ce scénario reflétait la réalité. En principe, ce recyclage devrait durer relativement longtemps, car une étoile comme le Soleil demeure dans la phase géante rouge pendant des centaines de millions d’années, nous donnant ainsi une chance de l’observer. Quelles seraient les signatures observationnelles ? En théorie, on devrait essentiellement voir le disque d’accrétion : la matière dans le disque est particulièrement échauffée par la friction, au point que le disque peut devenir nettement plus brillant que l’étoile compagne qui l’alimente. Ces disques deviennent tellement chauds qu’ils rayonnent surtout en rayons X dont l’observation nécessite des télescopes spatiaux, car l’atmosphère ne laisse pas passer ces rayons (heureusement pour la vie). Ils devraient donc être assez difficiles à détecter. En lumière visible, on devrait cependant voir un spectre inhabituellement intense dans le bleu ; cela ne vous rappelle rien ?

5. Évolution d’un système binaire jusqu’à la formation d’un pulsar milliseconde du type veuve noire à dos rouge. Les âges indiqués en gras sont donnés à titre d’exemple plausible, mais dépendent de nombreux paramètres et peuvent grandement varier [7]. (G. Voisin, CC BY-SA 4.0)
De fait, il existe bien des objets qui rayonnent fortement en rayons X. Les étoiles normales ne rayonnent pas beaucoup de rayons X, elles ne sont pas assez chaudes pour cela, mais un disque d’accrétion autour d’un objet compact le peut. Il existe une catégorie de sources X où l’on peut détecter de petites étoiles, quelques dixièmes de masse solaire, avec le même genre de modulation que montre le compagnon* de J1023. Par l’étude de ces modulations orbitales, on peut en déduire approximativement la masse de l’objet accréteur : entre une et deux masses solaires habituellement. On appelle ces objets « binaires X de faible masse », car l’étoile compagnon est moins massive que l’objet accréteur (Low Mass X-ray Binary en anglais). Ces binaires ressemblent étrangement à notre système favori, si ce n’est pour le disque d’accrétion et le fait qu’aucun pulsar n’est en vue. On sait cependant qu’il y a un objet compact, invisible, entre une et deux masses solaires, et cela ne laisse, en l’état des connaissances actuelles, que deux possibilités : une étoile à neutrons ou un trou noir. Il est difficile, parfois impossible, de déterminer avec certitude la nature de l’astre accréteur, mais on sait qu’au moins dans certains cas, il s’agit d’une étoile à neutrons par les traces typiques que celles-ci laissent dans les observations.
Observer le rallumage d’un pulsar naguère éteint
A-t-on trouvé les astres qui se transformeront un jour en pulsar milliseconde, ce que l’on appelle leurs progéniteurs ? Presque. Il n’est pas évident que, lorsque toute la matière du disque d’accrétion aura été accrétée sur l’étoile, celle-ci sera encore en mesure de rayonner comme un pulsar. Le champ magnétique pourrait avoir été dissipé ou enterré par la matière s’accumulant sur l’étoile, empêchant la formation de la magnétosphère sans laquelle un pulsar n’est qu’une simple étoile à neutrons inerte et le plus souvent invisible. En même temps, vérifier que les binaires X de faible masse se transforment bien en pulsar milliseconde supposerait de voir la transition, phénomène a priori très court à l’échelle de la vie de l’étoile, et donc très rare, ce qui rend les chances de l’observer quasi nulles.
Est-ce vraiment le cas ? Rappelez-vous, avant d’être détecté comme un pulsar milliseconde, J1023 était considéré comme une naine blanche avec un disque d’accrétion et une étoile compagnon, système de la famille des variables cataclysmiques. Cette famille de systèmes ressemble en fait beaucoup aux binaires X, à la différence que l’objet central est moins compact, rendant le disque d’accrétion moins chaud et moins lumineux. Il est par conséquent possible de confondre une binaire X peu lumineuse avec une variable cataclysmique plutôt intense. Et si, quelque part entre 2001 et 2007, c’est-à-dire entre la date de la dernière observation du disque d’accrétion et la découverte du pulsar, l’on avait en fait observé la transition entre la phase de recyclage et la résurrection du pulsar, plus rapide que jamais ? Cela se serait déroulé en l’espace de quelques années au maximum, c’est-à-dire rien en comparaison de l’âge du système, ou même des quelques centaines de millions d’années qu’une étoile comme le Soleil passe dans la phase géante rouge. Nous aurions donc eu une chance absolument extraordinaire ! Cependant, il est possible que la transition soit beaucoup plus longue, constituée d’un grand nombre de transitions dans les deux sens : de binaire X de faible masse en pulsar milliseconde, et de pulsar milliseconde en binaire X de faible masse. Les astronomes se sont donc armés de patience et ont commencé à surveiller régulièrement J1023, guettant le moindre signe de nouvelle transition.
C’est en juin 2013, entre deux observations effectuées à seulement deux semaines d’intervalle, que cela s’est produit : les pulsations radio ont disparu, le spectre visible très bleu et le scintillement sont revenus, le pulsar J1023 s’est de nouveau assoupi, le disque d’accrétion est revenu. Au moment d’écrire ces lignes, nous attendons impatiemment son réveil, certain que le chronométrage des pulsations radio nous dira comment l’orbite a changé au cours de la phase d’accrétion, de combien la rotation du pulsar a été accélérée. D’ici là, l’étude des modulations jour-nuit et ellipsoïdale nous en apprendra un peu plus sur les conditions extrêmes auxquelles le compagnon est soumis, et peut-être nous permettra de comprendre si oui ou non l’araignée engloutira un jour son compagnon jusqu’à la dernière bouchée.
Glossaire
Binaire ou Système binaire. Un système de deux étoiles orbitant l’une autour de l’autre.
Compagnon / étoile compagne. Dans une binaire, l’étoile la moins massive. Dans le cas des binaires considérées dans cet article, l’étoile compagne est toujours une étoile normale, alors que l’étoile la plus massive est une étoile à neutrons.
Étoile à neutrons. Résidu de certaines étoiles massives (plus de 8 fois la masse du Soleil) après leur explosion en supernova. Sous l’effet de la gravité, la masse de l’étoile (environ 1,5 masse solaire) est écrasée en un astre d’environ 20 km de diamètre. À une telle densité, les noyaux d’atomes subissent des réactions nucléaires transformant une grande partie d’entre eux en neutrons, d’où le nom de l’étoile.
Étoile normale. On entend ici une étoile qui, comme le Soleil, est une boule de plasma d’hydrogène et d’hélium dont l’énergie rayonnée provient des réactions de fusion nucléaire en son cœur.
Magnétosphère. La magnétosphère est la zone autour d’un astre où son champ magnétique domine sur les champs provenant de l’extérieur et détermine le comportement du plasma qui s’y trouve. Ainsi, de nombreux corps possèdent une magnétosphère, dont la Terre, le Soleil, ou encore Jupiter et son satellite Io. Les corps qui n’ont pas de champ magnétique, comme la Lune ou Mercure, n’ont donc pas de magnétosphère. Dans le cas des pulsars, le champ magnétique est immense, typiquement jusqu’à 109 teslas (10 000 milliards de fois le champ terrestre), ce qui leur donne des propriétés très particulières.
Pulsar. Un pulsar est une étoile à neutrons qui génère un signal sous forme d’impulsions (des « flashs » lumineux) se produisant selon la période de rotation de l’étoile. Généralement détectés en ondes radios, les pulsars peuvent aussi émettre à toutes les autres longueurs d’onde, mais seulement de façon exceptionnelle en lumière visible. On pense que la lumière n’est le plus souvent pas produite par l’étoile à neutrons elle-même, mais par le plasma piégé dans sa magnétosphère (voir ci-dessus). La magnétosphère tourne avec l’étoile et l’observateur voit une impulsion lorsque le faisceau pointe dans sa direction, expliquant la périodicité du signal. va ici
Notes
[1] Lorsque deux étoiles orbitent l’une autour de l’autre, chacune tourne autour du centre de gravité commun avec une même période, de sorte qu’elles se font toujours face. Le rapport entre les distances au centre de gravité des deux étoiles est déterminé par l’inverse du rapport de leurs masses. Ainsi, connaître l’orbite d’une seule des deux étoiles revient à connaître l’orbite de sa compagne également.
Références :
[1] Thorstensen et Armsrong, 2005
[2] Woudt, Warner et Pretorius, 2004
[4] Bond et al., 2002
[5] Backer et al., Nature, 1982
[6] Alpar et al., Nature, 1982
[7] Chen et al., The Astrophysical Journal, 2013

par Sylvain Bouley | Oct 13, 2022 | Zoom Sur
Toutes les étoiles tournent sur elles-mêmes. Mais à quelle vitesse ? Et surtout comment tournent-elles à l’intérieur ? Cette dernière question est longtemps restée tout à fait mystérieuse pour les astrophysiciens, faute de pouvoir mesurer cette rotation interne.

Et pourtant, comme on l’expliquera plus bas, la rotation influence l’évolution des étoiles. Pour « connaître » une étoile de façon précise, et en particulier mesurer sa masse ou son âge, il est donc nécessaire de savoir comment elle tourne sur elle-même et de prendre en compte les effets de la rotation sur son évolution. La question a son importance, car de plus en plus de disciplines en astrophysique ont un besoin crucial d’estimations fines des paramètres stellaires, comme leur masse, leur rayon ou leur âge. L’exemple le plus parlant est celui des exoplanètes, qui nécessitent pour être bien caractérisées de connaître précisément les propriétés de l’étoile autour de laquelle elles gravitent. C’est le cas aussi pour la compréhension de la formation et de la dynamique de notre Galaxie (une discipline connue sous le nom d’archéologie galactique), qui a besoin d’estimations précises des âges stellaires. Notre connaissance de la rotation interne des étoiles a connu un remarquable bond en avant ces dernières années grâce à l’astérosismologie des étoiles géantes rouges, c’est-à-dire l’étude des ondes sismiques qui se propagent dans ces étoiles. Nous vous proposons donc ici un voyage vers le centre des étoiles géantes rouges. Pour cela, on aura besoin de s’attarder en chemin sur la rotation stellaire et sur les principes de l’astérosismologie.
Les étoiles tournent sur elles-mêmes plus ou moins rapidement selon leur âge, leur masse et les conditions dans lesquelles elles se sont formées. Or, la rotation influence la structure et l’évolution des étoiles. Sa conséquence la plus spectaculaire est l’aplatissement des étoiles aux pôles du fait de la force centrifuge. Cet effet n’est toutefois visible que pour les étoiles qui tournent assez vite sur elles-mêmes. Le Soleil, qui a une rotation lente, est presque pratiquement sphérique (son diamètre aux pôles est inférieur à son diamètre équatorial de seulement 0,001%). En revanche, même dans les étoiles qui tournent lentement, la rotation provoque des mouvements d’ensemble à l’intérieur de l’étoile et induit ainsi un mélange des éléments chimiques. Cela modifie la quantité d’hydrogène disponible pour les réactions nucléaires au cœur de l’étoile et la rotation influence le rythme auquel l’étoile évolue.
Or, malgré leur importance, les effets de la rotation sont décrits de manière approximative et incomplète dans les modèles d’évolution stellaire actuels1. La première raison est que ces modèles sont pour l’instant contraints de supposer que les étoiles possèdent une symétrie sphérique, alors que la rotation rompt cette symétrie, en donnant à l’étoile une direction privilégiée (celle de son axe de rotation). On doit donc pour le moment se résigner à modéliser de façon approchée les effets de la rotation dans ce contexte simplifié. Un autre problème vient du fait que dans les étoiles, la rotation est intimement liée à d’autres processus physiques qui sont eux-mêmes imparfaitement compris. C’est le cas de la convection thermique, qui assure une partie du transport de chaleur dans certaines régions des étoiles (par exemple dans l’enveloppe du Soleil), ou des champs magnétiques, qui sont détectés dans une proportion grandissante d’étoiles. L’interaction entre la rotation et ces processus est un sujet très actif de recherche en physique stellaire. Pour progresser dans notre compréhension de ce problème épineux, il est aujourd’hui crucial d’obtenir des mesures observationnelles de la rotation dans les étoiles.
Mesurer la rotation des étoiles
Mesurer la rotation des étoiles n’est pas chose aisée. La majorité des méthodes actuelles permet d’estimer la rotation de surface de l’étoile. Pour cela, on peut par exemple se servir des taches stellaires (analogues des taches solaires) visibles à la surface des étoiles actives. À mesure que l’étoile tourne, ces taches passent périodiquement sur la face visible et impriment une modulation de la luminosité de l’étoile détectable par des observations photométriques, c’est-à-dire en mesurant le flux qui provient de l’étoile. La période du signal nous donne alors une estimation de la période de rotation de surface. Une autre méthode consiste à utiliser la spectroscopie : par effet Doppler, la rotation de surface provoque un élargissement caractéristique des raies spectrales : plus l’étoile tourne vite, plus les raies sont élargies2.
Toutefois, mesurer la rotation de surface des étoiles n’est pas suffisant pour comprendre les mécanismes qui gouvernent son évolution. En effet, il ne faut pas oublier que les étoiles ne sont pas des corps solides, mais des boules de gaz. Il n’y a donc a priori aucune raison que toutes les régions d’une étoile mettent le même temps à effectuer un tour complet autour de l’axe de rotation, comme ce serait le cas par exemple pour une boule de billard. Ainsi, on sait que la surface du Soleil met environ 24 jours à effectuer une rotation complète à l’équateur, mais plutôt environ 35 jours aux pôles : la rotation des étoiles varie donc en fonction de la latitude : on parle de rotation différentielle en latitude. De même, les couches centrales d’une étoile peuvent tourner à des vitesses différentes de celles des couches superficielles (rotation différentielle radiale). À première vue, on s’attend même à trouver des écarts importants entre la rotation au cœur des étoiles et celle à la surface. En effet, le cœur des étoiles tend à se contracter au cours de l’évolution (ce phénomène est particulièrement prononcé à certaines étapes de l’évolution de l’étoile, comme pour les géantes rouges, qui nous intéresseront plus loin). Or, si l’on contracte un corps isolé, sa fréquence de rotation (le nombre de tours qu’il effectue par seconde) augmente3. Par exemple, ce phénomène s’observe très bien dans le mouvement du patineur artistique qui tourne sur lui-même : il augmente sa fréquence de rotation en rapprochant les bras de son corps et la diminue en écartant les bras. On s’attend donc a priori à ce que le cœur des étoiles tourne plus vite que leur enveloppe. On voit donc que pour comprendre la rotation des étoiles, il est absolument nécessaire de mesurer leur rotation interne en plus de leur rotation de surface.
À ce stade, les choses se compliquent. En effet, quand on observe une étoile, on ne « voit » que les couches les plus superficielles, l’intérieur stellaire étant opaque au rayonnement à cause des interactions très fréquentes entre les photons et la matière. L’intérieur des étoiles est donc inaccessible aux observations directes. C’est cette constatation qui a poussé Arthur Stanley Eddington, un des pères de la physique stellaire moderne, à affirmer en 1926 que « l’intérieur des étoiles et du Soleil semble à première vue moins accessible aux investigations scientifiques que n’importe quelle autre région de l’Univers. Nos télescopes peuvent sonder de plus en plus loin les profondeurs de l’espace ; mais comment pourrions-nous avoir connaissance de ce qui est caché derrière des barrières substantielles ? Quel instrument peut percer les régions superficielles d’une étoile et en sonder l’intérieur ? » La réponse nous est parvenue seulement quelques décennies plus tard, avec l’avènement de l’héliosismologie, c’est-à-dire l’étude des oscillations du Soleil. Avant de montrer comment les oscillations peuvent donner accès à la rotation interne des étoiles, il est utile d’introduire brièvement la sismologie des étoiles, autrement appelée astérosismologie.
Astérosismologie
À regarder le ciel nocturne, il est tentant d’imaginer les étoiles comme des sources immuables de lumière. Et pourtant, une grande proportion d’entre elles présente des vibrations, qui sont généralement trop faibles pour être perçues à l’œil nu, mais nous apparaissent de plus en plus précisément à mesure que la sensibilité de nos instruments de mesure augmente4. Ces oscillations sont produites par la propagation d’ondes sismiques à l’intérieur des étoiles. Il en existe essentiellement deux catégories. Celles qui nous sont les plus familières sont les ondes de pression (ou ondes acoustiques). Elles sont directement équivalentes au son, c’est-à-dire aux ondes sonores se propageant dans l’atmosphère terrestre. L’autre type d’ondes que l’on rencontre dans les étoiles correspond aux ondes de gravité. Elles résultent de la poussée d’Archimède (la force qui fait flotter les objets moins denses que le liquide dans lequel ils se trouvent). Les vagues se propageant à la surface de la mer sont un exemple d’ondes de gravité.
Les ondes sismiques sont réfléchies à la surface ou aux interfaces entre les différentes régions de l’étoile. À certaines fréquences particulières, les ondes peuvent se superposer et donner naissance à des oscillations globales de toute l’étoile : on parle de modes propres d’oscillation. Ce phénomène est bien connu sur Terre, puisqu’on le rencontre par exemple dans les instruments de musique. Lorsqu’un musicien souffle dans une flûte, cela provoque des vibrations globales de la colonne d’air dans l’instrument à des fréquences qui lui sont propres : la fréquence fondamentale (qui donne la note) et les harmoniques (qui caractérisent le timbre de l’instrument). De la même façon que la flûte, une étoile peut, si elle reçoit une excitation particulière, vibrer selon ses modes propres d’oscillation. Pour les modes construits à partir d’ondes acoustiques, on parle de « modes de pression » ou de « modes p ». Les modes résultant de la superposition d’ondes de gravité sont dits « modes de gravité », ou « modes g ». On verra plus loin qu’il existe des modes qui possèdent une double identité, « p » et « g ». Il existe en théorie une infinité de modes d’oscillation dans une étoile, mais le nombre et la nature des modes qui sont effectivement excités dépendent du type d’étoile que l’on considère. Mesurer les fréquences des modes propres donne des informations sur sa structure interne, qui auraient été inaccessibles sans cela. Pour comprendre la manière dont l’astérosismologie nous renseigne sur les intérieurs stellaires, on peut poursuivre l’analogie avec la flûte. La fréquence de la note émise par l’instrument dépend de la vitesse du son cs dans l’air et de la longueur L de la colonne d’air dans la flûte. Plus la longueur L est grande, plus la fréquence de la note est basse et donc plus le son émis est grave. De même, plus L est petit, plus le son est aigu. Inversement, si la longueur L est connue, on peut directement déduire une estimation de la vitesse du son dans l’air à partir de la mesure de la fréquence de la note émise. De la même façon, la fréquence de chaque mode d’oscillation d’une étoile nous apporte des informations directes sur les propriétés physiques de l’étoile dans les régions qu’il sonde. Voilà qui répond brillamment au défi d’Eddington !

Figure 1. Comportement en surface de différents modes d’oscillation pour une étoile en rotation lente (comme le soleil ou les géantes rouges). Quand les zones en bleu se contractent, les zones en rouge se dilatent et inversement. Les régions en blanc correspondent à des «lignes nodales» des oscillations, qui par définition ne sont pas affectées par l’oscillation. Pour le lecteur avisé, l’allure des modes en surface correspond aux «harmoniques sphériques», que l’on retrouve par exemple en mécanique quantique dans la description des orbitales atomiques. elles sont caractérisées par deux nombres quantiques, le degré angulaire l (qui correspond aux nombres de lignes nodales du mode) et le nombre azimutal m (qui correspond aux nombres de méridiens qui sont des lignes nodales).
À quoi une étoile qui oscille ressemble-t-elle alors ? Les oscillations les plus simples que l’on puisse imaginer sont celles qui voient la surface entière de l’étoile se contracter puis se dilater périodiquement. Ce sont les oscillations radiales. Mais il en existe beaucoup d’autres, pour lesquelles des parties de la surface se contractent pendant que d’autres se dilatent (les oscillations non radiales). La figure 1 donne un aperçu de quelques types d’oscillations possibles. Pour comprendre cette figure, il faut se représenter que les zones en bleu se contractent pendant que les zones en rouge se dilatent, et inversement au cours de l’oscillation. La surface d’une étoile pulsante correspond à la superposition de tous les modes d’oscillation qui sont excités et peut donc avoir une allure très complexe.
Qu’en est-il alors du comportement des ondes sismiques à l’intérieur de l’étoile ? C’est ce qui nous intéresse directement ici, car c’est de cette façon que l’on obtient des renseignements sur la structure interne de l’étoile. Pour le comprendre, il est instructif de prendre l’exemple du Soleil, dont les oscillations n’ont été détectées qu’au début des années 19605. La figure 2 montre le chemin suivi par les ondes de pression dans le Soleil. Comme on le voit, elles se propagent dans les régions externes de l’étoile. Elles ont un déplacement quasiment vertical aux environs de la surface, mais à mesure qu’elles pénètrent dans l’étoile, elles subissent une déviation qui les ramène vers la surface6. Elles ont donc une profondeur de pénétration maximale, qui n’est pas la même d’un mode à l’autre : plus le degré angulaire l (voir définition sur la figure 1) des modes de pression est élevé, plus le mode est confiné dans les régions superficielles de l’étoile. Ce point est crucial, car il montre que les modes d’oscillation sondent des régions différentes de l’étoile. On comprend donc qu’en combinant les fréquences d’un grand nombre de modes, on peut obtenir des informations localisées sur les propriétés physiques de l’intérieur de l’étoile !
Contrairement aux ondes de pression, les ondes de gravité sont piégées dans le cœur de l’étoile. Elles ne peuvent pas se propager dans les zones convectives, c’est-à-dire les régions où la convection thermique transporte une partie de la chaleur. Or, le Soleil possède une enveloppe convective qui représente environ 30 % de son rayon. Les modes de gravité solaires possèdent donc des amplitudes extrêmement faibles à la surface de l’astre. Ces modes sont aujourd’hui activement recherchés, car ils renseigneraient sur la structure des régions les plus centrales de notre étoile. Il existe à ce jour plusieurs détections annoncées des modes de gravité solaires (Garcia et al. 2004, Fossat et al. 2017), mais celles-ci restent toutefois débattues.

Figure 2. Propagation des ondes sismiques de pression (a) et de gavité (b) dans un modèle du soleil.
a/ Chemin suivi par des ondes de pression de fréquence 3 mHz et de degré angulaire l = 5 (bleu), l = 30 (violet) et l = 100 (rouge). – b/ Les lignes en pointillé indiquent la profondeur de pénétration maximale des ondes. Chemin suivi par une onde de gravité de fréquence 200μHz et de degré angulaire l = 10.
Sismologie et rotation
Une étape cruciale pour le sujet qui nous intéresse ici est que les fréquences des modes d’oscillation sont modifiées par la rotation de l’étoile. Dans une étoile sans rotation, tous les modes d’oscillation qui se trouvent sur une même rangée sur la figure 1 (et donc qui possèdent le même degré angulaire l) ont la même fréquence. Sous l’effet de la rotation, leurs fréquences deviennent différentes et l’écart de fréquence entre ces modes est d’autant plus important que la rotation est rapide. En mesurant ces écarts, on a donc la capacité de mesurer la rotation à l’intérieur de l’étoile ! Or, il faut garder en tête que les modes d’oscillation sondent des régions différentes de l’étoile et chacun renseigne donc sur la rotation dans une région bien spécifique de l’étoile. Si l’on dispose de suffisamment de modes d’oscillation, on peut reconstituer le profil de rotation interne de l’étoile en rassemblant les informations venant de tous les modes. Jusqu’à très récemment, ce type de travail n’avait été possible que pour le Soleil.
Rotation interne du Soleil
La meilleure mesure sismique de la rotation interne d’une étoile est sans conteste celle du Soleil. Plusieurs centaines de modes d’oscillation ont pu être détectés et la séparation en fréquence causée par la rotation a été mesurée pour les modes non radiaux. Or, ces modes sondent des régions suffisamment distinctes les unes des autres pour pouvoir mesurer la rotation interne du Soleil. La figure 3 montre le profil de rotation interne du Soleil, qui est indubitablement une des plus grandes réussites de l’héliosismologie (Schou et al. 1998, Garcia et al. 2007) ! Cette figure représente une coupe du Soleil dans un plan méridien et les niveaux de couleurs indiquent la vitesse de rotation obtenue par l’héliosismologie. Les modes p solaires sont peu sensibles à la rotation aux pôles et dans les régions centrales de l’étoile, ce qui explique l’absence de mesure de rotation dans ces zones. On remarque sur la figure 3 une différence claire de comportement entre deux régions distinctes du Soleil.
Dans l’enveloppe convective (régions au-dessus de la ligne en pointillé), la rotation ne dépend presque pas de la profondeur dans l’étoile. En revanche, elle varie en fonction de la latitude, les pôles tournant plus lentement que l’équateur (période de rotation d’environ 25 jours à l’équateur et de 34 jours vers 70° de latitude). Les mesures sismiques sont donc en bon accord avec les mesures de rotation de surface provenant de l’étude des taches solaires, mentionnées plus haut.
Dans les régions internes du Soleil (en-dessous de la ligne en pointillé), la rotation est quasiment uniforme en rayon et en latitude : tous les éléments du gaz mettent le même temps pour effectuer un tour complet dans cette région.
Ces observations sont en contradiction directe avec les prédictions des modèles d’évolution stellaire standard, selon lesquelles la rotation angulaire (le nombre de tours effectués par seconde) doit augmenter à mesure qu’on se rapproche du cœur de l’étoile. L’héliosismologie a donc mis en évidence l’existence d’un processus qui homogénéise efficacement la rotation dans le Soleil et qui manque dans les modèles stellaires actuels. Comprendre de quel mécanisme il s’agit et la manière dont il opère est l’un des principaux défis en physique stellaire aujourd’hui. Pour progresser, il est crucial d’avoir accès à des mesures de rotation interne d’autres étoiles que le Soleil.
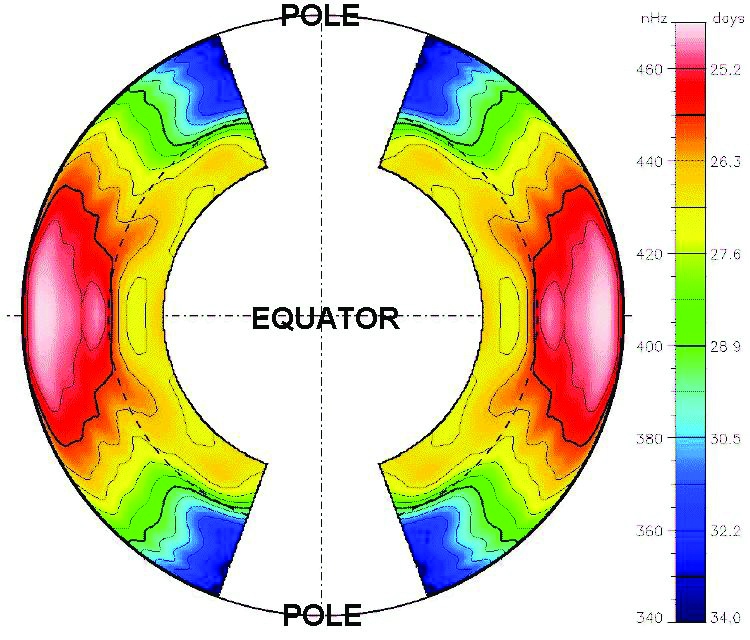
Figure 3. Profil de rotation interne du soleil obtenu par l’héliosismologie. La vue correspond à une coupe dans un plan méridien de notre étoile et les niveaux de couleurs indiquent le taux de rotation du plus lent (bleu) au plus rapide (rouge). La ligne en tirets indique la base de l’enveloppe convective du soleil. Dans les zones qui restent blanches, la rotation n’a pas pu être mesurée pas les auteurs (aujourd’hui, les modes p solaires permettent de mesurer la rotation jusqu’à environ 20 % du rayon solaire). (Schou et al. 1998)
Modes d’oscillation mixtes dans les étoiles géantes rouges
La sismologie des étoiles géantes rouges, qui a connu un essor spectaculaire au cours de la dernière décennie, a apporté un éclairage nouveau et des contraintes observationnelles inédites à ce problème de longue date. Il est utile de rappeler pour commencer que la phase de « géante rouge » pour une étoile survient après l’épuisement de l’hydrogène en son cœur (il s’agit donc de l’avenir lointain du Soleil). L’étoile possède alors un cœur constitué presque exclusivement d’hélium. Elle doit s’adapter à l’extinction des réactions nucléaires en son centre. Les régions internes se contractent et chauffent jusqu’à ce que l’hydrogène qui subsiste au-delà du cœur commence à fusionner pour donner de l’hélium. Parallèlement, les régions externes s’étendent fortement et refroidissent : l’étoile devient alors une géante rouge7. Ces étoiles sont particulièrement intéressantes pour le problème qui nous occupe ici, pour deux raisons.
La première est que les contractions et dilatations subies lors de la phase de géante rouge doivent en principe causer une forte rotation différentielle dans l’étoile : en se contractant, le cœur devrait tourner de plus en plus vite sur lui-même et, au contraire, l’enveloppe en expansion devrait tourner de moins en moins vite. Si, comme dans le Soleil, un mécanisme agit pour homogénéiser la rotation interne, il doit réduire la rotation différentielle dans les étoiles géantes. Mesurer la rotation de ces étoiles permettrait alors d’estimer l’efficacité de ce mécanisme et éventuellement de l’identifier.
La seconde raison de l’intérêt des géantes rouges est que ces étoiles possèdent des modes d’oscillation dits mixtes, qui sont à la fois des modes p et des modes g. La figure 4 présente la répartition en énergie d’un mode mixte dans une étoile géante. On voit que le mode mixte possède de l’énergie dans l’enveloppe, et plus particulièrement vers la surface. Dans cette région, il se comporte comme un mode p. Mais le mode possède également de l’énergie dans le cœur, où il a le comportement d’un mode g. L’apparition de modes mixtes dans les étoiles géantes est due au fait que les fréquences des modes g deviennent similaires à celles des modes p qui sont excités. En cela, les géantes rouges diffèrent des étoiles plus jeunes, comme le Soleil, pour lesquelles les modes g ont une fréquence nettement plus basse que celle des modes p.
Les modes mixtes ont un intérêt très clair : d’une part, leur caractère de modes g leur permet de sonder les régions les plus centrales de l’étoile, qui seraient inaccessibles autrement. D’autre part, leur caractère de mode p dans l’enveloppe leur donne des amplitudes détectables en surface, contrairement aux modes g solaires. Le très fort intérêt des modes mixtes avait été reconnu très tôt d’un point de vue théorique (Aizenman et al. 1977), mais il a fallu attendre l’avènement de l’astérosismologie spatiale pour que ces modes soient détectés et exploités à leur plein potentiel. Le premier coup d’accélérateur a été donné par le satellite CoRoT, lancé par le Cnes en 2006 avec le double objectif de sonder les intérieurs stellaires par la sismologie et de rechercher des exoplanètes. En observant de façon quasiment continue pendant des temps allant jusqu’à 180 jours, il a fourni des données sismiques d’une qualité sans précédent (la précision obtenue sur la mesure des fréquences des modes d’oscillation est inversement proportionnelle au temps d’observation). Il a ainsi permis la détection d’oscillations excitées par l’enveloppe convective dans des centaines de géantes rouges alors que seulement une poignée d’étoiles de ce type étaient connues auparavant (de Ridder et al. 2009). Le satellite Kepler, lancé par la Nasa en 2009, a transformé l’essai en augmentant ce nombre à environ 20 000 géantes rouges pulsantes. Des modes d’oscillation mixtes ont été détectés dans la plupart de ces étoiles (Deheuvels et al. 2010, Beck et al. 2011), ouvrant une fenêtre sans précédent sur le cœur de ces étoiles ! Ces modes ont apporté un éclairage nouveau sur de nombreux problèmes en physique stellaire.

Figure 4. répartition de l’énergie d’un mode mixte dans une étoile géante rouge. Les zones bleu foncé correspondent aux régions d’énergie maximale du mode. on voit que le mode possède de l’énergie dans l’enveloppe, et plus particulièrement vers la surface : il se comporte comme un mode p dans cette zone. il possède aussi de l’énergie au cœur, où il a le comportement d’un mode g.
Rotation interne des étoiles géantes rouges
En observant pendant quatre ans un même champ du ciel, le satellite Kepler a atteint une précision suffisante pour détecter et mesurer la séparation en fréquence causée par la rotation sur les modes mixtes (Beck et al. 2012). Cela a offert l’occasion excitante de sonder la rotation interne des étoiles géantes rouges. Les modes mixtes qui se comportent plutôt comme des modes de pression renseignent sur la rotation de l’enveloppe, alors que ceux qui ont un comportement de mode de gravité fournissent une mesure de la rotation dans les régions centrales. De telles mesures étaient ardemment attendues, dans la mesure où même pour le Soleil nous ne disposons pas de mesure ferme de la rotation au cœur !
La première étoile géante rouge pour laquelle il a été possible de mesurer précisément la rotation du cœur est une étoile cible de Kepler (Deheuvels et al. 2012). Nous l’avons baptisée Otto, d’après le professeur Otto Lidenbrock, qui mène l’expédition vers les profondeurs terrestres dans Voyage au centre de la Terre, de Jules Verne. L’astérosismologie a permis de montrer que le cœur de cette étoile tourne entre 12 et 22 fois plus vite que son enveloppe. Cette rotation différentielle radiale peut paraître forte, mais en réalité elle est environ 100 fois plus faible que celle prédite par les modèles stellaires actuels (Ceillier et al. 2013, Marques et al. 2013). C’est là une preuve claire qu’un processus physique œuvre pour empêcher le cœur des géantes rouges de tourner trop vite.
Par la suite, il a été montré que lorsque les étoiles sont en train de devenir des géantes rouges (on parle alors d’étoiles sous-géantes), la rotation du cœur accélère alors que la rotation de l’enveloppe décélère au cours de l’évolution. Les résultats qui mènent à cette conclusion sont montrés sur la figure 5. Ce type de comportement était attendu, dans la mesure où le cœur se contracte alors que l’enveloppe se dilate pendant cette période (souvenez-vous de l’exemple du patineur !). Toutefois, à la fois la vitesse de rotation au cœur et l’intensité de la rotation différentielle radiale (le rapport entre la rotation du cœur et celle de l’enveloppe) sont nettement inférieures à ce que prédisent les modèles théoriques actuels. Cela confirme l’existence d’une homogénéisation de la rotation interne à ce stade de l’évolution.
La rotation du cœur a également pu être mesurée dans un millier d’étoiles géantes rouges (Mosser et al. 2012, Gehan et al. 2018). Ces résultats ont montré que la rotation au cœur des étoiles géantes rouges subit une légère décélération au cours de l’évolution malgré la contraction rapide du cœur, qui devrait au contraire fortement l’accélérer ! Là encore, ces observations pointent vers l’existence d’un mécanisme qui tend à réduire la rotation au cœur des étoiles géantes.
Alors qu’au début des années 2010, le Soleil restait la seule étoile dont la rotation interne avait pu être sondée, l’astérosismologie des géantes rouges a apporté des mesures de la rotation au cœur de plus d’un millier d’étoiles à diverses étapes de leur évolution. Cela constitue une mine d’or pour revisiter la question épineuse de l’évolution temporelle de la rotation interne des étoiles !

Figure 5. Évolution de la rotation au cœur (points rouges) et dans l’enveloppe (points bleus) au cours de la phase de sous-géante (lorsque l’étoile est en train de devenir une géante rouge). La quantité donnée en abscisse (log g) correspond à la gravité de surface de l’étoile. Plus une étoile géante est évoluée, plus sa gravité de surface est faible. Par conséquent, une étoile évolue de la gauche vers la droite dans ce diagramme. on voit que, globalement, le cœur accélère et l’enveloppe décélère au cours de l’évolution pendant la phase de sous-géante.
Perspectives
Ces nouveaux résultats n’ont pas tardé à motiver de nombreuses nouvelles études théoriques visant à identifier le mécanisme qui opère dans les géantes rouges. Le problème n’est pas encore résolu, mais de grands progrès ont ainsi été obtenus. Deux principaux candidats sont aujourd’hui à l’étude. Le premier est le champ magnétique. Il est probable que les cœurs stellaires abritent des champs magnétiques, qu’ils soient présents dès la formation de l’étoile ou bien engendrés par un phénomène de dynamo (comme c’est le cas dans l’enveloppe du Soleil ou dans le noyau de la Terre). Or, de tels champs magnétiques pourraient lisser la rotation interne des étoiles, par exemple par le développement d’instabilités de ces champs magnétiques. L’autre mécanisme possible est la génération d’ondes de gravité internes à la base de l’enveloppe convective des étoiles géantes. Dans ces enveloppes, la matière stellaire est turbulente. Les mouvements turbulents à la base de l’enveloppe peuvent exciter des ondes de gravité, qui se propagent vers le cœur de l’étoile. Dans certaines conditions, ces ondes peuvent homogénéiser la rotation entre l’endroit où elles sont générées (sous l’enveloppe convective) et l’endroit où elles se dissipent. De nombreux travaux théoriques et simulations numériques sont aujourd’hui en cours pour tester ces deux hypothèses et déterminer si elles peuvent rendre compte de la rotation interne des étoiles géantes.

Figure 6. De nouvelles données sismiques seront bientôt complétées par celles de missions comme Plato lancée par l’Europe.
La moisson de résultats en astérosismologie est très loin d’être finie ! En plus des résultats sur les géantes rouges, d’autres types d’étoiles ont récemment vu leur rotation interne révélée par l’astérosismologie, comme les étoiles de type spectral A et B en séquence principale (étoiles plus massives que le Soleil et qui fusionnent encore de l’hydrogène au cœur) ou les naines blanches. Les données sismiques des satellites CoRoT et Kepler seront bientôt complétées par celles du satellite américain TESS (lancé par la Nasa en 2018 et en cours d’opération) et du satellite européen PLATO (Esa), dont le lancement est prévu en 2026. On aura à terme une vision claire de la rotation interne des étoiles et de la manière dont elle est modifiée au cours du temps. Avec, à la clé, tous les ingrédients pour comprendre comment la rotation influence l’évolution des étoiles et le décrire correctement dans les modèles d’évolution stellaire.
Sébastien DEHEUVELS | Institut de recherche en astrophysique et planétologie
Notes:
- Modèles d’évolution stellaire : programmes informatiques permettant de résoudre les équations de la structure et de l’évolution stellaire de façon numérique. Ce sont ces modèles qui permettent aux astrophysiciens de donner des estimations de grandeurs telles que la masse et l’âge des étoiles, qui ne sont en général pas directement mesurables par les observations. 2. En fait, dans ce cas, on ne mesure pas directement la vitesse de rotation, mais sa projection sur la ligne de visée. 3. En mécanique, c’est la conséquence de la conservation du moment cinétique pour un corps isolé. 4. Attention, il ne faut pas confondre les oscillations des étoiles avec le scintillement apparent des étoiles dans le ciel nocturne. Ce dernier est produit par le passage des photons dans l’atmosphère terrestre, alors que les oscillations stellaires, elles, sont intrinsèques aux étoiles. 5. Il faut préciser que les oscillations solaires sont de très faible amplitude. Elles correspondent à une variation de l’ordre du millionième de la luminosité de l’étoile. 6. Cette déviation est due au fait que la matière stellaire n’est pas homogène : la vitesse du son augmente à mesure que les ondes pénètrent dans l’intérieur de l’étoile. Les ondes de pression se propageant dans l’intérieur de la Terre lors d’un séisme subissent le même type de déviation. 7. On la qualifie de géante « rouge » car sa surface refroidit et rayonne alors principalement dans l’infrarouge. Elle nous apparaît donc avec un éclat tirant sur le rouge.

par Sylvain Bouley | Oct 13, 2022 | Zoom Sur
Les étoiles. Quand on regarde le ciel, elles sont là, immuables, presque rassurantes, toujours fidèles au rendez-vous. De toute éternité, semble-t-il. Pourtant, les étoiles ont bien une « vie ». Elles « naissent », « vieillissent », puis « meurent ». Environ dix nouvelles étoiles se forment chaque année dans notre Galaxie, la Voie lactée, qui en compte la bagatelle de cent milliards. Mais comment les étoiles se forment-elles ? À partir de quelle matière ? Comment leurs caractéristiques, notamment leur masse, sont-elles déterminées ? Quels rôles jouent-elles dans l’histoire de l’Univers ? C’est à toutes ces questions, dont nous verrons qu’elles sont centrales pour notre compréhension du monde, que nous tenterons de répondre ici.
Disons-le d’emblée, les étoiles sont LE grand moteur de l’Univers, de l’Univers complexe en tout cas. En effet, au sortir du Big Bang, il n’existe qu’un très petit nombre d’éléments chimiques : l’hydrogène et l’hélium, bien sûr et, hormis quelques traces infimes de lithium et de deutérium, c’est pratiquement tout. Pas de quoi aller bien loin, donc. En comparaison, un rapide coup d’œil au tableau périodique des éléments, aussi appelé tableau de Mendeleïev, nous en dévoile plus d’une centaine.
Une étoile, ça « sert » à quoi ?
Ce sont bien entendu nos étoiles qui sont les grands alchimistes du cosmos. En effet, seuls les cœurs stellaires, confinés par la gravité, sont en mesure de fournir les températures et les densités nécessaires pour allumer les réactions nucléaires qui engendreront des éléments nouveaux. Pierre philosophale de la toute première heure, elles font beaucoup mieux que transformer le plomb en or : les étoiles transforment l’hydrogène… en vie ! Enfin, en ses briques dans un premier temps. Les étoiles sont en effet responsables de la synthèse de pratiquement tous les éléments, par exemple, et pour ne citer qu’eux, de l’oxygène et du carbone. Ces éléments chimiques sont absolument essentiels à l’émergence de la complexité moléculaire, qui commence avec des molécules aussi modestes que le monoxyde de carbone (CO), l’eau (H2O), ou encore l’ion moléculaire HCO+ et se poursuit jusqu’aux molécules du vivant telles que l’ADN. Précisons que ces atomes et ces molécules, avant même de permettre la vie, jouent un rôle de premier plan dans la structuration des galaxies et même pour la formation des étoiles. En effet, atomes et molécules amènent le milieu interstellaire à se refroidir, c’est-à-dire à émettre des photons qui emportent leurs excès d’énergie, abaissant ainsi la température du gaz et facilitant, voire permettant, la contraction de ce dernier.
Mais les étoiles sont beaucoup plus que de simples alchimistes cosmiques, elles donnent également naissance aux planètes puis dispensent à ces dernières la chaleur et la lumière qui permettent, en tout cas sur Terre, à la vie de se développer puis de prospérer. En effet, les planètes naissent dans des disques de gaz et de poussière qui, comme on le verra plus en détail par la suite, apparaissent autour de l’étoile au moment où elle se forme. Une fois ce disque dissipé, un système planétaire est né. La durée de vie d’une étoile telle que notre Soleil étant de plusieurs milliards d’années, période durant laquelle il évolue très peu (on dit qu’il est sur la séquence principale), les planètes bénéficient d’un environnement très stable, ce qui, si elles se trouvent à la bonne distance de leur étoile pour avoir de l’eau à l’état liquide, comme la Terre, permet à la vie d’évoluer. Rappelons simplement ici que l’on a aujourd’hui observé directement plus de quatre mille planètes autour d’autres étoiles (fig. 1 et 2) et que, selon des arguments statistiques, on estime que le nombre d’exoplanètes dans la Galaxie est un peu supérieur à celui des étoiles.

1. Une planète récemment observée. L’étoile centrale est masquée afin de rendre l’observation possible. (ESO/J. Rameau)

2. Une naine brune (au centre) et sa planète. C’est la première fois qu’une planète est observée autour d’un objet aussi peu massif. (ESO)
La recette de la formation des étoiles
L’histoire commence dans le grand vide galactique. En fait, la nature en ayant horreur, de vide, il n’y a point. La Galaxie est remplie d’un gaz, composé pour l’essentiel d’hydrogène et d’hélium, encore appelé milieu interstellaire. Ce dernier est une composante importante de notre Galaxie puisque sa masse totale, à peu près dix milliards de masses solaires, est d’environ 10 % de celle des étoiles. Il s’agit là d’un fluide très complexe qui donne beaucoup de fil à retordre aux physiciens depuis plus d’un siècle ! En effet, le milieu interstellaire est un environnement multiphasique. En certains endroits, il peut être extrêmement brûlant, avec des températures atteignant le million de kelvins, alors qu’ailleurs il peut tomber au-dessous des dix kelvins, ce qui en fait l’une des régions les plus froides de l’Univers. Ces contrastes de température se conjuguent avec des contrastes de densité tout aussi extrêmes : les régions chaudes sont les plus ténues, ne contenant parfois que quelques milliers d’atomes par mètre cube, alors que les plus denses en contiennent plusieurs dizaines de milliards.
De plus, le milieu interstellaire, à la manière d’un torrent impétueux, est « turbulent », c’est-à-dire animé de mouvements aléatoires, et ce sur des distances allant du millier d’années-lumière jusqu’à la seconde-lumière. De surcroît, il présente un nombre de Mach élevé, c’est-à-dire que la vitesse du fluide est plusieurs fois supérieure à la vitesse du son. Ces mouvements supersoniques, en conjonction avec la force gravitationnelle, le rendent fortement compressible. Pour couronner le tout, le milieu interstellaire est également baigné d’un champ magnétique (fig. 3) qui co-évolue avec lui. Ce champ magnétique, qui agit un peu à la manière d’une pelote d’élastiques, rend les mouvements du fluide anisotropes. Il est plus facile aux éléments du fluide de se mouvoir le long du champ magnétique que dans la direction transverse. Gravité, turbulence, magnétisme, phase, c’est dans ce contexte que nos étoiles apparaissent.
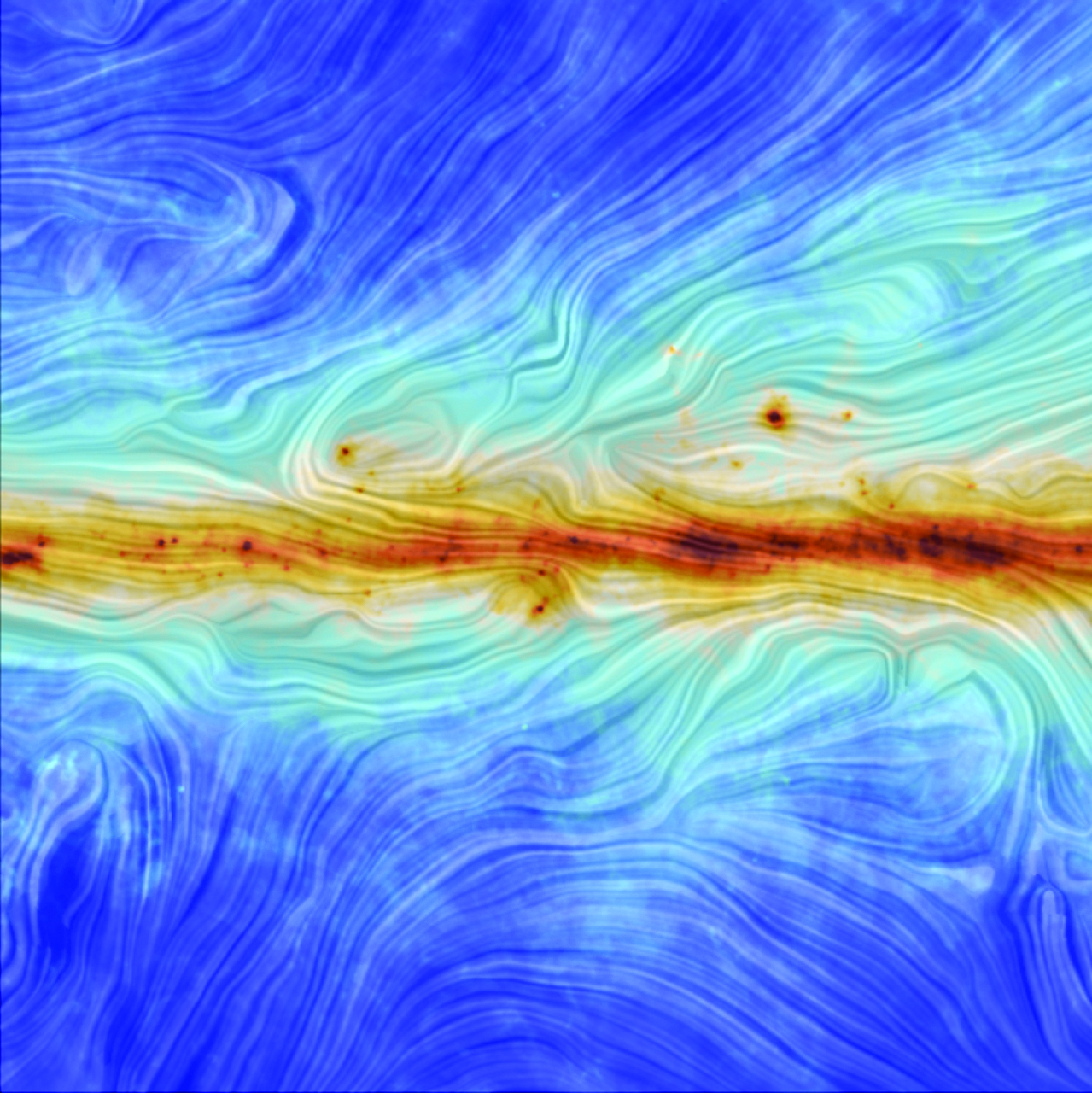
3. Le plan de la Galaxie observé par le satellite Planck. Les contours montrent la structure du champ magnétique galactique. (esA/Planck Collaboration. Acknowledgement: M.-A. Miville-Deschênes, CNRs – institut d’astrophysique spatiale, université Paris-Xi, orsay (France)
Plus précisément, les étoiles se forment dans les régions denses du milieu interstellaire, encore appelées nuages moléculaires (fig. 4). Ces derniers, qui doivent leur nom au fait que l’hydrogène s’y trouve sous forme de dihydrogène (H2), sont en effet de vastes étendues dont la forme évoque celle des nuages atmosphériques. Ces géants, que l’on trouve souvent sous forme de filaments ou d’une collection de filaments (fig. 5, fig. 6 et 7), ont une taille qui dépasse la centaine d’années-lumière et pèsent jusqu’à cent mille masses solaires. Sous l’influence de la force de gravitation, les parties les plus denses de ces nuages, encore appelées cœurs denses préstellaires (fig. 8), vont se contracter, subissant une véritable implosion, un effondrement au cours duquel leur densité va augmenter de manière vertigineuse. De quelques dizaines de milliards de particules par mètre cube, celle-ci va progressivement croître pour atteindre plusieurs milliards de milliards de fois cette valeur. Quant à la taille, initialement de l’ordre de l’année-lumière, elle va diminuer jusqu’à finalement atteindre environ un rayon solaire, soit approximativement deux secondes-lumière. Une étoile est née ! Bien entendu, l’ensemble du processus n’est pas instantané. Il faut quelques centaines de milliers, peut-être un million, d’années pour que le cœur dense préstellaire donne naissance à un embryon stellaire puis que celui-ci accrète la masse qui constituera l’étoile.

4. Le nuage moléculaire du Taureau. Il s’agit de l’un des nuages formant des étoiles, les plus proches et les mieux étudiés. (Five College Radio Astronomy observatory (FCRAo), Gopal Narayanan / Mark Heyer)

5. Un nuage sombre de poussière cosmique serpente sur cette image spectaculaire à grand champ, éclairé par la lumière brillante de nouvelles étoiles. Ce nuage dense est une région de formation d’étoiles appelée Lupus 3, où des étoiles d’une chaleur éblouissante naissent de l’effondrement de masses de gaz et de poussière. Cette image a été créée à partir d’images prises à l’aide du VLT Survey Telescope et du télescope MPG/ESO de 2,2 mètres. Il s’agit de l’image la plus détaillée prise jusqu’à présent de cette région.

6. Un filament massif du nuage moléculaire d’Orion observé par le satellite Herschel. La direction du champ magnétique observée par Planck est également représentée. – 7. Un filament de gaz moléculaire situé dans le nuage du Taureau. (eso/APeX (MPifR/eso/oso)/A. Hacar et al./Digitized sky survey 2. Acknowledgment: Davide De Martin) – 8. Globule Barnard 68. Ce nuage est si dense qu’il est autogravitant, c’est-à-dire qu’il est confiné par sa propre force de gravité. Il produira peut- être une étoile dans le futur, s’il finit par s’effondrer sur lui-même. (ESO) – 9. Un disque protoplanétaire (centre de l’image) vu par la tranche. Sa taille est de quelques centaines d’unités astronomiques. (ESO)
Des disques, des jets : rotation et champ magnétique !
La formation d’une étoile est en fait plus complexe qu’un simple effondrement. Au moins deux phénomènes, aussi spectaculaires qu’essentiels, sont également à l’œuvre. Ils trouvent tous deux leur origine dans la rotation… En effet, la matière interstellaire étant animée de mouvements turbulents, un nuage, une fois cette turbulence dissipée, hérite d’un certain moment cinétique qui, lui, ne se dissipe pas. Or, à l’instar d’un patineur qui accélère quand il ramène ses bras tendus vers son corps, un nuage en rotation qui se contracte tourne de plus en plus vite. Tellement vite que la force centrifuge, celle-là même qui empêche la Lune de tomber sur la Terre, finit par s’opposer à la gravité, stoppant pour un temps l’effondrement gravitationnel. La force centrifuge ne s’exerçant que dans le plan de la rotation, le gaz adopte alors la forme d’un disque appelé encore disque d’accrétion (fig. 9).
Se pose alors un problème crucial. Puisque le gaz est à présent à l’équilibre et que le moment cinétique est conservé, le gaz est « piégé » dans le disque. Comment parvient-il alors jusqu’à l’étoile ? D’une manière ou d’une autre, le moment cinétique du disque doit diminuer, ce qui n’est possible que si le disque parvient à évacuer ce moment vers l’extérieur. C’est là qu’un autre acteur majeur entre en lice : le champ magnétique. En effet, les lignes de champ magnétique, qui, rappelons-le, se comportent un peu comme des élastiques, permettent aux différentes particules de fluide d’échanger de la rotation via la « tension magnétique ». Cela a pour effet de ralentir le disque et de permettre au gaz de poursuivre sa course jusqu’à l’étoile. Il faut croire que ce mécanisme est réellement efficace, car le moment cinétique du Soleil est environ un million de fois plus faible que celui contenu initialement dans le cœur dense préstellaire. Autrement dit, le moment cinétique des particules qui composent le Soleil a diminué d’un facteur un million au moment de la formation de ce dernier. L’existence de ces disques est d’une grande importance car c’est en leur sein que se forment les planètes (fig. 10).

10. Observation réalisée avec ALMA du disque protoplanétaire autour de l’étoile HL Tauri. On y voit des sillons qui, bien que cela reste à confirmer, pourraient être liés à la présence de planètes. (AlMA-eso/NAoJ/NRAo) –
Le champ magnétique et la rotation du gaz engendrent un autre phénomène étonnant, les jets protostellaires (fig. 11 et 12). Comme leur nom l’indique, les jets sont constitués de gaz éjecté à grande vitesse, jusqu’à 200 km/s, du voisinage de l’étoile. À la manière d’un jet d’eau, ils sont souvent très directionnels. En fait, ce mécanisme d’éjection est assez général en astrophysique et on le trouve très souvent associé aux phénomènes d’accrétion. C’est également le cas par exemple pour les noyaux actifs de galaxies, qui sont constitués d’un trou noir géant et qui donnent naissance à des jets de la taille d’une galaxie (fig. 13). L’émission des jets et l’évolution du disque d’accrétion sont encore imparfaitement comprises. Elles semblent étroitement liées l’une à l’autre, le jet permettant sans doute au disque d’évacuer son excès de moment cinétique.

11. Une protoétoile et son jet. Elle se situe dans la partie la plus sombre de l’image et on voit le jet qui en émane de part et d’autre. (eso) – 12. Un jet émanant d’une très jeune étoile. Il s’étend sur plusieurs années-lumière. (eso/M. McCaughrean)

13. La galaxie lenticulaire Centaurus A. On voit un jet de plusieurs dizaines de milliers d’années-lumière de long. Ce jet est la conséquence du trou noir central de cette galaxie qui accrète du gaz et des étoiles. (eso/WFi (optical); MPifR/eso/APeX/A.Weiss et al. (submillimetre); NAsA/CXC/CfA/R.Kraft et al. (X-ray))
Les étoiles se forment en amas
Tout observateur un peu attentif remarque immédiatement, lors d’une nuit dégagée, que les étoiles, loin de se répartir uniformément sur la voûte céleste, ont une tendance certaine à se regrouper. Parmi les plus beaux exemples visibles à l’œil nu, on trouve les Pléiades ou encore Orion (les figures 14 et 15 en montrent deux exemples moins connus). Par ailleurs, c’est à présent bien établi, environ la moitié des étoiles sont binaires, c’est-à-dire qu’elles possèdent un compagnon auquel elles sont liées par la force gravitationnelle. Les étoiles auraient-elles un instinct grégaire ? En un sens, oui, et ce d’autant plus qu’elles sont jeunes. À bien y réfléchir, la raison en est assez simple. C’est une fois encore notre bonne vieille gravité, assistée sans doute par la turbulence, qui en est responsable. Ainsi qu’on le sait depuis Newton, la force de gravité décroît comme l’inverse du carré de la distance. Dans le jargon des physiciens, on dit que c’est une force à « longue portée », c’est-à-dire que son influence se ressent même sur de grandes distances.

14. Le superamas d’étoiles Westerlund 1. Situé à environ 12 000 années-lumière, cet amas possède des étoiles jeunes et massives. (ESO)

15. L’amas Arches est le plus dense connu à ce jour dans la Galaxie. Situé à une centaine d’années-lumière du Centre galactique, il est sans doute âgé de 2 millions d’années. (ESO/P. espinoza)
La conséquence est que l’effondrement gravitationnel d’un nuage est un événement complexe. Tout se passe comme si le nuage s’effondrait à la fois globalement et localement, et ce de manière relativement synchronisée, c’est-à-dire dans un intervalle de temps assez court. Il en résulte un groupe d’étoiles formées à peu près en même temps et dans une région très limitée. Autrement dit, ces étoiles sont liées entre elles par leur force de gravité, et ce lien, s’il est assez fort, peut durer très longtemps. Ainsi, les amas globulaires (fig. 16), qui sont sans doute les résidus de la formation des étoiles des premières galaxies, ont un âge qui atteint la dizaine de milliards d’années. On observe des amas de toutes les tailles, allant de quelques étoiles jusqu’à plusieurs centaines de millions. Néanmoins, dans la majorité des cas, les amas d’étoiles ne sont pas suffisamment liés et finissent par se désolidariser, soit spontanément quand les étoiles massives explosent en expulsant du gaz, soit sous l’influence du champ gravitationnel galactique, qui tend à les détruire petit à petit. Les étoiles de ces amas suivent alors des trajectoires différentes et finissent par se disperser, perdant toute trace de leur origine commune. Vraiment toute ? Peut-être pas, car les amas d’étoiles semblent remarquablement homogènes chimiquement. Les abondances des différents éléments chimiques sont donc très proches d’une étoile à l’autre d’un même amas, qui possède ainsi une certaine signature chimique. Il est donc théoriquement possible de retrouver les étoiles qui se sont formées au sein d’un même amas.

16. L’amas globulaire géant Oméga Centauri. Situé à environ dix-sept mille années-lumière, il comporte environ trois cent mille étoiles. (eso/iNAF- Vst/omegaCAM. Acknowledgement: A. Grado, l. limatola/iNAF-Capodimonte observatory)
Précisons que les étoiles binaires se forment, elles, peut-être par un mécanisme différent lié à la rotation et aux disques d’accrétion. Quand ceux-ci sont suffisamment massifs, il est en effet envisageable que l’instabilité gravitationnelle se développe au sein du disque et conduise à la formation d’une autre étoile dans le disque (fig. 17 ). Comme la taille du disque est d’environ cent unités astronomiques ou moins, le compagnon ainsi formé se situe à peu près à cette distance. Bien entendu, des phénomènes de migration peuvent avoir lieu et amener les étoiles de la binaire ainsi formée à se rapprocher ou, au contraire, à s’éloigner l’une de l’autre.

17. Un système multiple en cours de formation. Au centre de l’image se trouve une binaire. Un troisième objet orbite autour des deux autres. Le gaz est en rotation autour des deux étoiles centrales. L’ensemble constitue peut- être un disque d’accrétion qui s’est fragmenté sous l’influence de la force de gravité. La structure fait une centaine d’unités astronomiques de rayon. (AlMA (ESO/NAOJ/NRAO)/J.J. tobin (University of oklahoma/leiden University)
Des grosses, des petites : tout un éventail de masses
Notre étoile, le Soleil, qui possède une masse d’environ 2.10^30 kg, soit environ 400 000 fois la masse de la Terre, est une étoile assez banale. Des étoiles, il en existe des grosses, jusqu’à au moins 200 fois la masse du Soleil, et des petites, moins d’un dixième de masse solaire. En fait, il en existe même de plus petites, enfin pas tout à fait de « vraies » étoiles. Pourquoi ? Elles sont trop peu massives pour que puisse avoir lieu la réaction nucléaire impliquant la conversion de l’hydrogène en hélium. Elles brûlent tout de même un élément, le deutérium, sorte de gros atome d’hydrogène contenant, en plus de son proton, un neutron. Ces astres, encore appelés naines brunes, peuvent donc avoir une masse beaucoup plus petite, un centième de masse solaire, peut-être même moins. Les étoiles et les naines brunes couvrent donc un spectre de masse qui s’étale sur plus de quatre ordres de grandeur et il est même possible que des étoiles encore plus grosses puissent exister, aucun mécanisme connu ne s’y opposant.
Pour autant, cela ne signifie pas, bien entendu, que toutes ces étoiles soient en nombre comparable. C’est même très loin d’être le cas. Les étoiles les plus abondantes sont plus petites que notre Soleil, environ trois fois moins massives. Ainsi, les étoiles moins massives que cette valeur deviennent de moins en moins nombreuses, jusqu’à même devenir rares pour les naines brunes de plus faible masse. De même, plus les étoiles sont massives, moins elles sont nombreuses. Les observateurs ont même trouvé que le nombre d’étoiles diminue comme leur masse à la puissance 2,3. Cette valeur, qui est connue depuis 1955, reste mal comprise sur le plan théorique. Elle joue pourtant un rôle absolument fondamental dans l’histoire de l’Univers car, on le verra par la suite, les étoiles de masses différentes ont des comportements et des propriétés bien spécifiques. Les idées les plus modernes pour expliquer la distribution de masse des étoiles mettent en avant le rôle de la gravité ainsi que celui de la turbulence. Cette dernière crée des fluctuations de la densité du gaz qui sont ensuite amplifiées par la gravité. Elle tend alors à les isoler du reste de l’écoulement et induit leur effondrement.
Comme on le pressent assez naturellement, les caractéristiques d’une étoile dépendent fortement de sa masse. Par exemple, la luminosité d’une étoile, c’est-à-dire le nombre de photons émis depuis la surface à chaque seconde, est proportionnelle au cube de sa masse. Cela signifie qu’une étoile de dix masses solaires brille comme mille Soleils ! Cette forte dépendance est une conséquence de la loi dite du corps noir. Cette loi bien connue en physique stipule qu’un tel corps – un four bien isolé en est un exemple – rayonne comme sa température à la puissance quatre. Or, il se trouve qu’une étoile est un excellent corps noir . Contrairement à ce que l’on pourrait croire, une étoile est en effet très opaque. Les photons qui voyagent dans une étoile ne cessent de se heurter aux électrons et aux noyaux : ils doivent véritablement se frayer un chemin jusqu’à la surface. Plusieurs dizaines de milliers d’années leur sont nécessaires pour faire un trajet qui leur prendrait deux secondes dans le vide !
Cette forte dépendance de la luminosité à la masse de l’étoile n’est pas sans conséquence. En effet, rayonner coûte de l’énergie à une étoile. Chaque photon émis tend à la refroidir et, pour maintenir sa température élevée, elle doit puiser dans ses ressources. Ces dernières n’étant pas infinies, elles finissent par s’épuiser. Dans une étoile, la seule source d’énergie vient des réactions nucléaires, celles-là mêmes qui convertissent l’hydrogène en éléments lourds. L’énergie émise provient en fait de la légère perte de masse qui a lieu au cours de ces transformations selon la célèbre formule E = mc2. Ainsi, la réserve en énergie d’une étoile est proportionnelle à sa masse. Mais comme, rappelons-le, la luminosité dépend du cube de la masse, cela signifie que le temps mis pour consommer toute l’énergie disponible, soit approximativement la durée de vie de l’étoile, est donc inversement proportionnel au carré de la masse de l’étoile.
Les grosses étoiles, en particulier, vivent un temps très court. Une étoile de dix masses solaires vit environ cent millions d’années ; les plus grosses étoiles connues vivent environ quatre millions d’années. À l’échelle cosmique, c’est un temps dérisoire. Rappelons par exemple que le Soleil, aujourd’hui âgé de cinq milliards d’années, en vivra encore cinq autres. Quant aux petites étoiles, elles vivent donc plus longtemps que le Soleil. Ainsi une étoile de 0,7 masse solaire vit plus de quinze milliards années, l’âge de l’Univers. Les petites étoiles sont donc virtuellement immortelles ! Les premières à s’être formées sont toujours présentes. Elles constituent autant de fossiles cosmiques, témoins privilégiés des débuts de l’Univers, encore peu en mesure de former des étoiles. Bien entendu, elles sont activement recherchées par les astronomes.

18. Le reste de la supernova 1987A vu par l’interféromètre ALMA. (AlMA:eso/NAoJ/NRAo/A.)
La formation des étoiles : un processus diablement inefficace
À chaque instant, quantité d’événements ont lieu au sein des galaxies : le ballet des étoiles qui tournent, celui du gaz qui bouillonne, explose ou jaillit. Comment comprendre et quantifier toute cette agitation ? Parmi tous les chiffres auxquels on peut penser, il en est un qui continue de faire l’objet d’une attention toute particulière ; on peut même dire que c’est l’un des graals de l’astrophysique contemporaine. Il s’agit du taux de formation des étoiles (star formation rate en anglais). Cette quantité décrit simplement le nombre d’étoiles formées en une année. Étant donné le rôle majeur joué par les étoiles, on comprend bien pourquoi elle est si importante. Les observations montrent que dans le cas de notre Galaxie par exemple, environ dix nouvelles étoiles, soit en masse l’équivalent de trois nouveaux Soleils, se forment chaque année. Les astrophysiciens essaient depuis plus d’un demi-siècle de comprendre ce résultat en apparence simple… sans y parvenir.
L’origine du problème est la suivante : la force de gravité qui s’exerce dans un milieu agit en un temps caractéristique, encore appelé temps de chute libre. En substance, c’est le temps que le milieu en question met pour s’effondrer sur lui-même. Dans le cas du gaz pouvant former des étoiles dans la Galaxie, ce temps vaut à peu près un million d’années. Par ailleurs, la masse de gaz dense est, elle, de l’ordre d’un milliard de masses solaires. En divisant cette masse par le temps de chute libre, on s’attendrait à avoir une estimation du taux de formation d’étoiles; or, un calcul élémentaire conduit à la valeur de mille masses solaires par an, ce qui est trois cents fois supérieur à la valeur observée ! La conclusion qui s’impose est donc que le gaz dans la Galaxie n’est pas en chute libre. Un ou plusieurs processus physiques s’opposent à la force de gravité. En dépit de nombreux efforts, cinquante années de recherche n’ont pas permis d’élucider avec précision la raison de cette inefficacité, même si des progrès importants ont été réalisés.
Plusieurs pistes ont été explorées. Ainsi, on a d’abord proposé que le champ magnétique, encore lui, pouvait expliquer le faible taux de formation d’étoiles. Pour ce faire, l’intensité magnétique doit être élevée, de sorte que la force magnétique domine la force gravitationnelle. Or, bien que le champ magnétique soit une quantité difficile à mesurer, l’acharnement des astrophysiciens a fini par révéler que ce dernier était sans doute trop faible pour s’opposer efficacement à la gravité. Dans un second temps, une nouvelle hypothèse a été explorée, la turbulence. Les mouvements désordonnés du fluide constituent un obstacle pour la gravité et, s’ils sont assez forts, ils peuvent même l’empêcher d’agir. Néanmoins, la turbulence a cette particularité qu’elle se dissipe rapidement : à peine une particule de fluide a-t-elle le temps de traverser le nuage, que déjà l’intensité de la turbulence a très fortement décru. Il faut donc des sources puissantes pour, sans cesse, régénérer la turbulence, et ce sont ces sources qui font défaut ici.
La dernière hypothèse, toujours en cours d’investigation, est que la rétroaction exercée par les jeunes étoiles formées, particulièrement les massives, disperse le gaz et limite l’efficacité de la gravité. De quoi s’agit-il exactement ? Les étoiles au cours de leur vie, et plus particulièrement à leur début et à leur fin, dégagent des quantités importantes d’énergie sous forme de rayonnement ou de matière. On a déjà évoqué les jets qui accompagnent très souvent les processus d’accrétion. Il y a également le rayonnement très intense des jeunes étoiles. Il peut ioniser le gaz environnant (fig. 19 et 20) et de ce fait le chauffer jusqu’à des températures de milliers de degrés. Ces bulles chaudes et ionisées repoussent alors le gaz du nuage dans lequel l’étoile est née et finissent par le détruire. Enfin, les étoiles massives en fin de vie émettent des vents puissants et finissent par exploser en supernovae (fig. 18). Ces dernières émettent en un temps très court une quantité gigantesque d’énergie et deviennent même plus lumineuses que la Galaxie. Une fantastique onde de choc est émise, créant une bulle de trois cents années-lumière. Bien entendu, une telle explosion n’est pas sans conséquence sur les nuages de gaz qui se trouvent à proximité. Ceux-ci sont dispersés, ce qui arrête instantanément la formation des étoiles.

19. Le nuage moléculaire de la nébuleuse d’Orion est ionisé par le rayonnement produit par les étoiles massives situées à proximité.
Les modèles actuels, qui prennent en compte l’ensemble de ces phénomènes – champ magnétique, turbulence et rétroaction stellaire –, obtiennent des taux de formation stellaire en bien meilleur accord avec les observations, quoique sans doute encore trop élevés. Du fait de la complexité du problème et des difficultés à le modéliser, la raison de ce désaccord n’est pas encore bien claire. Est-ce dû à un processus manquant ou à une insuffisance dans les calculs ? Les recherches continuent.

20. Les Piliers de la création pris par le télescope Hubble dans le visible (gauche) et l’infrarouge (droite). Situées dans la nébuleuse de l’Aigle, ces structures de gaz sont érodées par le rayonnement ionisant dû aux étoiles massives proches. (ESO)
L’écologie galactique
Gravité, turbulence, champ magnétique, rétroaction stellaire, rayonnement, chimie : la formation des étoiles implique de nombreux processus, de nombreux champs du savoir. Tous ces phénomènes interagissent, « se couplent », dit-on en physique. De plus, les échelles spatiales impliquées vont de la centaine d’années-lumière, soit la taille des nuages moléculaires géants, jusqu’à la seconde-lumière, soit la taille d’une étoile. C’est à peu près comme si l’on comparait la taille de la Terre et celle d’une fourmi. Nombreux processus physiques, grandes dynamiques d’échelles, formation de structures, rétroaction, voilà un ensemble qui n’est pas dissociable de ses parties. Un ensemble cohérent qui n’est pas sans rappeler, sur le principe uniquement bien sûr, la complexité du climat terrestre. À ce titre, il n’est sans doute pas exagéré de parler d’un écosystème galactique. De fait, les galaxies présentent une organisation qui va bien au-delà des nuages moléculaires géants dont nous avons déjà mentionné l’existence et le rôle dans la formation des étoiles (fig. 21).
Pour bien percevoir qu’une telle organisation est bien à l’œuvre, examinons quelques échelles de temps. On l’a déjà dit, notre Galaxie possède environ un milliard de masses solaires de gaz moléculaire. Comme par ailleurs elle forme environ trois masses solaires d’étoiles par an, cela implique qu’en moins d’un milliard d’années, notre Galaxie aura épuisé son gaz. Or, notre Galaxie est âgée de dix milliards d’années et tout laisse penser que durant ce laps de temps, sa vie a été en tout point identique à ce qu’elle est aujourd’hui. Il y a donc une contradiction apparente. Dans le même ordre d’idée, si l’on tient compte de toutes les générations d’étoiles qui ont déjà vécu, l’enrichissement du gaz interstellaire en éléments lourds (carbone, oxygène…) devrait être bien supérieur à ce qu’il est aujourd’hui. Une conclusion s’impose : notre Galaxie continue de grossir… Du gaz intergalactique pauvre en éléments lourds, celui-là même qui à l’origine forma la Voie lactée, continue, sous l’influence du champ gravitationnel galactique, de tomber sur celle-ci, venant se mélanger au milieu interstellaire galactique. En fait, on estime que la Galaxie reçoit environ trois masses solaires de gaz chaque année, de sorte que le gaz transformé en étoiles est remplacé par ce gaz venu du milieu dit intergalactique.
L’image qui peu à peu émerge est donc celle de galaxies nourries par du gaz primordial qui se mélange au gaz galactique, sous l’influence de la force de gravité assistée par les mouvements turbulents. Ce gaz s’assemble en nuages géants, puis en cœurs préstellaires qui s’effondrent et forment des étoiles. Ces dernières synthétisent les éléments chimiques lourds puis les dispersent à la fin de leur vie, notamment lors des explosions de supernovae. Ces éjecta se mélangent au gaz ambiant en même temps qu’ils détruisent les nuages moléculaires. Après un grand brassage, ce gaz finira par se contracter de nouveau, poursuivant ainsi le cycle de la matière interstellaire. Bien entendu, toutes les galaxies ne sont pas identiques à la nôtre, certaines forment encore beaucoup plus d’étoiles, d’autres n’en forment pratiquement plus aujourd’hui. Toutes, néanmoins, connaissent ou ont connu une phase active de formation d’étoiles et un cycle de la matière interstellaire. Comme l’histoire de la formation des étoiles varie d’une galaxie à l’autre, voire d’un endroit à l’autre d’une même galaxie, on s’attend à ce que l’abondance des éléments chimiques lourds, encore appelée « métallicité », varie, et c’est précisément ce qui est observé. La métallicité varie de moins d’un dixième, de la valeur dite solaire, c’est-à-dire correspondant à la composition de notre Soleil, à plus de trois fois cette valeur.

21. La galaxie spirale NGC1232. Plusieurs bras spiraux sont visibles. Ils contiennent des nuages moléculaires qui forment activement des étoiles. (eso)
Notre Univers est donc très profondément organisé et structuré par les étoiles. Des galaxies aux planètes, en passant par les nuages de gaz interstellaires, toutes les structures subissent leurs influences. Pour reprendre l’expression chère à Hubert Reeves, nous sommes bien des « poussières d’étoiles ». Comprendre l’histoire et les détails de leur formation, c’est comprendre la grande mécanique de l’Univers et la toute première étape de notre propre histoire.
Patrick Hennebelle | AIM – CEA
Pour aller plus loin
- Derek Ward-Thompson, Anthony P. Whitworth, An Introduction to Star Formation, Cambridge University Press, 2011. ISBN 9780521630306.
- Steven W. Stahler, Francesco Palla, The Formation of Stars, Wiley-VCH, janvier 2005, p. 865. ISBN 3-527-40559-3.
- Christopher McKee, Eve Ostriker, « Theory of Star Formation », Annual Review of Astronomy & Astrophysics, vol. 45, Issue 1, p. 565-687.
- Patrick Hennebelle, Edith Falgarone, « Turbulent Molecular Clouds », The Astronomy and Astrophysics Review, vol. 20, article id. 55.
- James Lequeux, avec la contribution de Edith Falgarone et Charles Ryter, Le Milieu Interstellaire, EDP Sciences, coll. « Savoirs actuels ».








































