La physique des étoiles à neutrons révélée par les pulsars

par Sylvain Bouley | Oct 16, 2023 | Zoom Sur

Samedi 25 mars, Jocelyn Bell Burnell a reçu à Paris le prix Jules-Janssen 2022 de la Société astronomique de France. En 1967, Jocelyn Bell préparait une thèse en radioastronomie sous la direction d’Antony Hewish. Sans l’avoir cherché, elle découvrit un signal d’un genre encore jamais observé, et qu’elle analysa. C’était le premier pulsar ; il fut baptisé CP 1919. Sa découverte allait prouver l’existence des étoiles à neutrons, objets de spéculations rigoureuses remontant aux années 1930, mais à l’observation desquelles tous les astronomes avaient renoncé. Nous allons montrer ici le lien entre les étoiles à neutrons et les pulsars.

Dans les livres d’initiation à l’astronomie, il est très courant de décrire les étapes de l’existence d’une étoile comme celles d’une vie : elles commenceraient par naître, subir une sorte d’enfance, puis une vie d’adulte plus routinière mais active, et finissant par mourir. Dans les cours d’astronomie, les auteurs emploient plutôt les mots formation, évolution, catastrophes, et phase de dégénérescence. Mais parfois, dans le résumé d’un chapitre, le parallèle biologique peut revenir soudain avec une phrase comme : « Les étoiles de grande masse initiale finissent leur vie en supernovas [1]. » Pourquoi pas ? Mais de quoi parle-t-on en évoquant la mort ? Pour un animal, un humain, c’est une cessation totale d’activité, suivie, sauf dans de rares cas, d’un recyclage complet de la matière l’ayant composé, au bénéfice d’autres êtres vivants. D’un mort il ne reste rien sur Terre, sinon des souvenirs, et éventuellement une descendance.

Alors, si l’on fait ce parallèle, quand une étoile meurt-elle ?

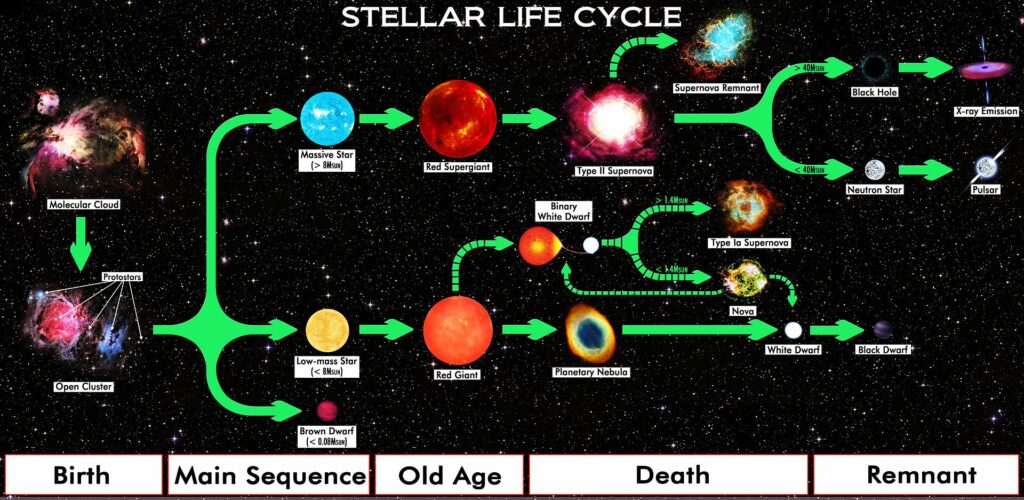
Représentation de l’évolution d’une étoile en la comparant à celle d’un être vivant avec les phases de naissance (birth), vieillesse (old age) et mort (death). Selon cette terminologie, pour les étoiles de masse initiale supérieure à 8 masses solaires (massive stars), les étoiles à neutrons sont les restes (remnant) d’une étoile morte. Pourtant, ces restes présentent une activité observable parfois plus longtemps que celle de l’étoile lorsqu’elle était dans la séquence principale. (R.N. Bailey – CC BY 4.0, Wikimedia)

La mort nucléaire d’une étoile

Les étoiles dont la masse dépasse huit fois celle du Soleil brillent à peine plus de 20 ou 30 millions d’années. C’est peu en comparaison des dix milliards d’années attendues pour une étoile comme le Soleil. En effet, plus les étoiles sont massives, plus leur matière est comprimée sous leur propre poids, et moins leurs épaisses couches de matière empêchent le cœur de refroidir. Leurs régions internes sont donc très denses et chaudes, et cela favorise l’accomplissement rapide d’une succession de réactions nucléaires.

Les premières réactions qui font passer l’étoile de l’obscurité à la lumière transforment l’hydrogène en hélium. Ce faisant, elles libèrent de l’énergie sous forme de rayonnement gamma. Comme l’étoile est opaque, cette lumière de très haute énergie s’échappe difficilement des régions internes, ce qui fait monter la température. D’autres réactions nucléaires deviennent alors possibles. L’hélium se transforme en carbone, en azote, en oxygène. Ces réactions exigent des températures plus élevées, mais elles produisent aussi plus d’énergie par nouvel atome produit. à chaque fois, l’énergie libérée chauffe de plus en plus l’étoile. La pression est de plus en plus forte et pousse la matière vers l’extérieur. Si l’étoile a une masse de plus de huit fois celle du Soleil, le poids de l’étoile suffit à équilibrer les forces de pression. Bien que l’étoile passe par des phases de gigantisme où la pression l’emporte un peu sur la gravité, le cœur continue de chauffer, toujours écrasé sous la même masse de matière. Alors, l’hélium se transforme par fusion nucléaire en carbone, lui-même transformé en oxygène ; enfin, d’autres réactions nucléaires plus exigeantes en énergie permettent la fabrication d’éléments plus lourds, comme du silicium, de l’aluminium, et d’autres métaux.

La dernière étape est la formation de noyaux d’atomes de fer qui est un élément thermonucléairement inerte. Aucune libération d’énergie ne va plus dès lors s’opposer au processus de contraction du noyau. Les réactions nucléaires qui pourraient permettre de produire des atomes plus massifs que le fer libèrent moins d’énergie qu’elles n’en demandent. Alors, sous leur effet, la matière refroidit. En conséquence, les conditions de température exigées pour la poursuite des réactions nucléaires ne sont plus remplies et les réactions nucléaires cessent. Il n’y a donc plus de production de chaleur, ce qui diminue la pression. Sous l’effet de son propre poids qui n’est plus compensé par une pression suffisante, l’étoile commence à s’effondrer.

Il s’ensuit une explosion que l’on nomme « supernova ». Et comme cette explosion commence par l’effondrement de l’étoile sous son poids, ce sont les forces de gravitation qui initient le processus. On désigne donc cet événement comme une « supernova gravitationnelle ».

C’est à ce stade que le noyau de l’étoile massive se transforme en étoile à neutrons.

C’est aussi là que dans la métaphore avec le vivant, on fait mourir l’étoile. Pourtant, comme nous le verrons, ce qui reste après une supernova gravitationnelle n’est pas seulement la fin d’une histoire, ni un simple souvenir.

Mais pour comprendre d’où vient cette idée d’étoile à neutrons, faisons un saut de cent ans en arrière.

La découverte du neutron

James Chadwick (1891-1974), physicien atomiste anglais, travaillait à Cambridge sous la direction d’Ernest Rutherford. Rutherford avait découvert le proton en 1919, dont la masse était correctement estimée à environ 1 836 fois celle de l’électron.

On savait aussi qu’un atome est composé d’un noyau contenant des protons, entouré, bien plus loin, d’un cortège d’électrons ; or, la masse du noyau excède de beaucoup celle de ses protons. Par exemple, un noyau d’hélium a une masse proche de 4 (en masses de protons) mais seulement 2 protons. Il manque en masse l’équivalent de deux protons.

Fallait-il renoncer à la conservation de la charge, en considérant un noyau d’hélium formé de 4 protons, soit 2 protons « normaux » et 2 protons en plus annihilant leur charge ? Une autre solution moins révolutionnaire, proposée entre autres par Rutherford, supposait la présence de particules neutres dans le noyau. Chadwick les appela les neutrons. Il restait à les découvrir, et à les caractériser. Chadwick reprit une expérience menée par d’autres physiciens quelques années auparavant, et réalisa ce programme. Il publia en 1932 un article sobrement intitulé : « Possible Existence of Neutron ». En 1935, cette découverte lui valut le prix Nobel (lire l’encadré 1).

Mais bien avant 1935, seulement quelques mois après la publication de l’article de Chadwick, des astronomes se demandèrent si l’existence d’une étoile entièrement constituée de neutrons serait possible.

La découverte du neutron

Chadwick s’intéressa à une expérience initialement menée en 1930 par Walter Bothe* et Herbert Becker, où du béryllium est bombardé par des noyaux d’hélium issus du rayonnement cosmique. On avait constaté que les rayons cosmiques arrivant sur des éléments légers émettent des rayonnements « ultra-pénétrants », c’est-à-dire dont les effets se font sentir même à travers plusieurs centimètres de matière solide. Chadwick allait caractériser ces rayonnements. Ces derniers activent des réactions nucléaires. Quelle était leur nature ? Irène et Frédéric Joliot-Curie (1931)** développèrent une théorie supposant des rayons gamma de 50 MeV. En 1932, Chadwick reprit l’expérience. Avec l’hélium et le béryllium, les collisions produisent un noyau de carbone, et ce fameux rayonnement inconnu. Chadwick conclut de son étude que ces « rayonnements » étaient en fait des particules neutres (les neutrons), et la réaction observée était la suivante : 4He + 9Be → 12C + 1 neutron. Cette formule a le mérite de conserver le nombre de protons, le nombre de neutrons, de conserver la charge électrique. Son bilan énergétique permit à Chadwick de conclure que la masse des neutrons est 1,001 masse du proton, donc à peine supérieure à celle du proton. Il montra aussi que le neutron n’est pas la réunion d’un proton et d’un électron (comme le serait une sorte d’atome d’hydrogène ultra-compact), mais bien une particule en soi***.

* Lauréat du prix Nobel de physique en 1954. – ** Tous deux lauréats du prix Nobel de chimie en 1935. – *** Si un proton était la somme d’un électron et d’un proton, sa masse serait inférieure à la somme des deux masses – une partie de celle-ci étant prise par l’interaction entre les deux particules. Mais en fait, la masse du neutron est supérieure à celle des deux particules isolées. Après l’expérience de Chadwick, on a découvert que la fusion d’un proton et d’un électron produit un neutron plus un neutrino. Le neutrino de cette réaction est une autre manière de se convaincre que le neutron n’est pas la simple somme d’un proton et d’un électron.

Le cœur dégénéré des étoiles froides

Les années où l’on découvrit l’existence du neutron furent aussi celles où l’on posa les fondements de la physique quantique. La physique quantique permit de mettre en évidence deux grandes familles de particules, les bosons dont font partie les photons, et les fermions dont font partie les électrons, les protons et les neutrons ainsi que les neutrinos. Or, les fermions sont des particules qui doivent toutes être dans un état différent ; autrement dit, il n’y a pas deux neutrinos dans tout l’Univers qui soient dans le même état. Un état étant caractérisé par leur énergie, leur position et leur spin, il est impossible d’empiler un nombre quelconque de fermions (d’énergie finie) dans un petit espace (lire l’encadré 2).

Notons une propriété plutôt contre-intuitive : les fermions les plus légers sont ceux qui réclament le plus d’espace. Ainsi, l’espace qui permettra d’empiler N électrons devra être plus grand que l’espace permettant d’empiler N neutrons. Dans une étoile, lorsqu’elle refroidit quand il n’y a pas de réactions nucléaires pour la chauffer, cela prend une grande importance. En effet l’étoile ne s’effondre pas totalement puisque les fermions qui la constituent s’opposent à ce que toute la matière soit rassemblée dans un minuscule volume.

En raison de cette impossibilité, les assemblées de fermions (solides, liquides ou gazeuses) réagissent comme si elles étaient soumises à une force de pression pouvant devenir très forte quand on atteint de hautes densités. Cet effet est une pression, mais elle n’est plus contrôlée par la température. Elle dépend principalement de la densité des fermions les plus légers. On l’appelle la pression de Fermi, et la matière contrôlée par la pression de Fermi est dite « dégénérée ».

Considérons par exemple une étoile de masse semblable au Soleil, qui aurait cessé son activité nucléaire. La matière tombe vers le centre, augmentant sa densité, jusqu’à ce que la pression de Fermi devienne importante. Ce sont les électrons, les plus exigeants en espace, qui contrôlent cette pression. Donc, pour une étoile dégénérée comme le deviendra le Soleil, on atteint sous l’effet de la pression de Fermi des électrons une densité d’environ une tonne par centimètre cube. Les étoiles régies par la pression de Fermi des électrons sont bien connues des astronomes : ce sont les naines blanches, que les astronomes ont découvertes dans les années 1910. L’explication de leur extrême densité et du rôle de la pression de Fermi des électrons fut donnée par l’astronome britannique Ralph Fowler en 1927.

Mais voilà qu’au début des années 1930, un étudiant indien de Fowler, Subrahmanyan Chandrasekhar, décida d’appliquer les lois de la relativité restreinte aux naines blanches. Il découvrit qu’au-delà de 1,4 masse solaire, la pression de Fermi ne peut contrer les forces de gravité. Le physicien soviétique Lev Landau [2] découvrait indépendamment la même limite en 1932. Au-delà de cette masse, l’étoile doit s’effondrer. Mais en quoi ?

L’astronome (génial) qui régnait alors sur l’astronomie britannique, Sir Arthur Eddington, n’était pas convaincu de l’effondrement des naines blanches au-delà de 1,4 masse solaire. Il fit cette remarque demeurée célèbre, lors d’un congrès en 1935 : « Je pense qu’il doit exister une loi de la nature qui empêche une étoile de se comporter de façon aussi absurde. »

Cependant, d’autres physiciens s’étaient convaincus, suite à la découverte de Chadwick, qu’en éliminant les électrons, la nature pourrait former des gaz comportant uniquement des neutrons. Ce serait un gaz neutre, donc dépourvu de forces électriques, mais contrôlé par la pression de Fermi. Et comme celle-ci permet de mettre plus de neutrons dans un même volume, un gaz de neutrons serait beaucoup plus dense. Ainsi, l’on pourrait former des étoiles extrêmement denses composées uniquement, ou presque, de neutrons.

En 1932, Lev Landau s’était demandé si le cœur des étoiles, même les plus normales, pourrait être constitué d’un tel gaz de neutrons. La découverte quelques années plus tard des réactions nucléaires opérant au sein des étoiles lui donna tort. Mais si les bonnes idées meurent quelque part, elles renaissent souvent ailleurs. En 1934, deux astronomes travaillant aux États-Unis, Walter Baade et Fritz Zwicky, écrivirent un article très court, sans démonstration, où ils proposaient qu’il existerait des étoiles uniquement composées de neutrons, qu’elles seraient la phase ultime de l’évolution stellaire, que les supernovas seraient la transition entre les étoiles normales et les étoiles à neutrons, et (cerise sur le gâteau) que les supernovas seraient à l’origine des rayons cosmiques. Géniale intuition : bien que rien ne fût prouvé dans cet article, l’histoire allait montrer que les auteurs « avaient tout bon ».

Les particules qui se laissent empiler, et celles qui résistent

Les fondations de la mécanique quantique ont mis en évidence deux familles de particules, les bosons et les fermions. Elles se distinguent en pratique par leur capacité à « se laisser empiler ». Plus précisément, on considère les caractéristiques possibles des particules : leur vitesse ou leur énergie, leur position, et une grandeur qui ne se manifeste qu’en mécanique quantique : l’orientation de leur spin. Le spin, c’est comme si les particules étaient de minuscules toupies, et l’orientation du spin caractériserait leur axe de rotation. Par ailleurs, le spin de chaque particule a une valeur bien déterminée. Par exemple, 0 pour les photons, et 1/2 pour les électrons, les protons… et les neutrons. Cette valeur de spin est très importante, et les physiciens ont donné le nom de « bosons » aux particules ayant un spin entier, comme le photon, et le nom de « fermion » aux particules à spin demi-entier. La théorie de la mécanique quantique et les expériences montrent qu’il peut exister plusieurs bosons ayant exactement les mêmes caractéristiques. Donc, on peut en mettre beaucoup, avec la même énergie au même endroit. Par exemple, on peut (avec des lasers) avoir de grandes concentrations de photons ayant à peu près tous la même énergie. En revanche, il ne peut y avoir deux fermions ayant exactement les mêmes caractéristiques. C’est la propriété importante qui les distingue des bosons. On nomme souvent cette propriété « le principe d’exclusion de Pauli ». Il ne peut y avoir deux fermions au même endroit avec la même énergie, avec la même orientation de spin. Comme l’orientation de spin peut prendre deux valeurs, en considérant des neutrons de faible énergie, on ne peut pas en empiler un nombre infini dans un petit espace.

Comment une étoile peut-elle être formée majoritairement de neutrons ?

Une étoile normale est formée d’atomes. Ceux-ci contiennent des protons, des neutrons et des électrons. Comment cela peut-il donner à la fin une étoile formée seulement de neutrons ?

Sous l’effet des pressions formidables que subissent les étoiles dont le cœur dépasse la masse fatidique de Chandrasekhar de 1,4 masse solaire, il se produit une réaction au cours de laquelle un proton et un électron fusionnent, pour produire un neutron et un neutrino. Le neutrino est une particule extrêmement légère, électriquement neutre, soumise seulement à l’interaction faible.

Les supernovas gravitationnelles, comme mentionné au début du présent article, caractérisent le moment où ces réactions ont lieu. La majorité des neutrons soumis à l’effet de leur masse, à l’écrasement par la matière de l’étoile qui continue à leur tomber dessus et à des interactions de type nucléaire avec d’autres neutrons, restent dans l’étoile. En revanche, les neutrinos s’échappent. Il reste donc à la fin une étoile majoritairement formée de neutrons. On l’appelle donc simplement « une étoile à neutrons ».

Bien entendu, une étoile massive et dense comme une étoile à neutrons est soumise à des effets de gravitation extrêmement forts. Or, depuis 1916, on savait que dans le régime de gravitation forte, il faut renoncer à la théorie classique de Newton, mais appliquer la relativité générale d’Einstein. Alors, trois physiciens, Richard Tolmann, Robert Oppenheimer (le futur directeur du programme de la bombe atomique américaine) et George Volkoff, posaient les équations de l’équilibre d’une étoile sphérique uniquement composée de neutrons, dans le régime de la relativité générale. Ils les publièrent en 1939, ainsi que les solutions qu’ils obtenaient. On les considère toujours comme valides, et on les nomme les équations TOV, initiales des noms des trois auteurs. Les solutions qu’ils trouvaient donnaient une densité en effet assez proche de la densité du noyau atomique. D’un point de vue astronomique, c’était cependant assez décevant : une étoile à neutrons ne pouvait excéder 0,7 masse solaire (limite révisée depuis), et une telle étoile tiendrait dans une sphère d’une dizaine de kilomètres de rayon. Or, la luminosité d’une étoile, si elle dépend de la puissance 4 de sa température, est aussi proportionnelle à sa surface. Une si petite étoile a une surface minuscule. Même chauffées à quelques millions de degrés, les étoiles à neutrons s’avéraient inobservables avec les télescopes de l’époque.

Les étoiles à neutrons entrèrent donc dans le placard des idées théoriques un peu folles et invérifiables expérimentalement. On les plaçait même, vu leurs propriétés incroyables et excessives, sur l’étagère des monstres. Puis la Seconde Guerre mondiale donna aux physiciens des occupations plus urgentes (et monstrueuses également). Quelques années plus tard, même avec la fin de cette guerre, les étoiles à neutrons demeuraient hors du champ des préoccupations des astronomes « normaux[3] ».

Le sujet survivait cependant, avec des chercheurs comme John Archibald Wheeler, Fritz Zwicky qui ne renonçait pas à son idée, et Andrew Cameron.

Ils s’intéressaient par exemple au problème de la masse limite de 0,7 masse solaire. Si une supernova causait l’effondrement d’un cœur plus massif, qu’adviendrait-il des neutrons correspondant à la masse excédentaire ? Seraient-ils expulsés lors de l’explosion ? évaporés ? ou bien l’étoile continuerait-elle de s’effondrer… en trou noir ? un concept encore plus spéculatif à cette époque.

Ces auteurs comprirent que si l’étoile à neutrons atteint la densité du noyau atomique, alors les effets de l’interaction nucléaire devaient s’ajouter à la pression de Fermi des neutrons. Le problème était la relative ignorance que l’on avait (et que l’on a encore en partie) de l’interaction forte. Cependant, on fit des calculs en se fondant sur ce qu’on avait appris dans les accélérateurs de particules avec des interactions à trois neutrons… en les extrapolant avec astuce à un très grand nombre de neutrons. La masse limite des étoiles à neutrons fut repoussée à 2 ou 3 masses solaires. Cela ne les rendait toujours pas observables, mais au moins cela leur donnait une plus grande étendue de masses possibles, donc de plus grandes chances d’exister.

De nos jours, plusieurs modèles possibles d’intérieurs d’étoiles à neutrons ont été développés. Des observations ont déjà permis d’en éliminer certains, mais il en reste un très grand nombre, et tous ne supposent pas que le cœur d’une étoile à neutrons soit uniquement formé de neutrons. Il pourrait y avoir d’autres particules, considérées comme instables dans des conditions de pression moindres. Parmi tous ces modèles, il est possible que plus d’un soit correct, et qu’il existe en fait plusieurs types d’étoiles à neutrons. Notons que les neutrons sont formés de l’association de trois particules élémentaires, appelées des quarks up et down. Sous des densités encore plus élevées que dans les étoiles à neutrons, les neutrons se seraient eux-mêmes effondrés, laissant place à leurs composants élémentaires et formant un vaste mélange de quarks, que l’on appellerait une étoile à quarks, qui aurait une masse proche de celle des étoiles à neutrons et un rayon légèrement plus petit.

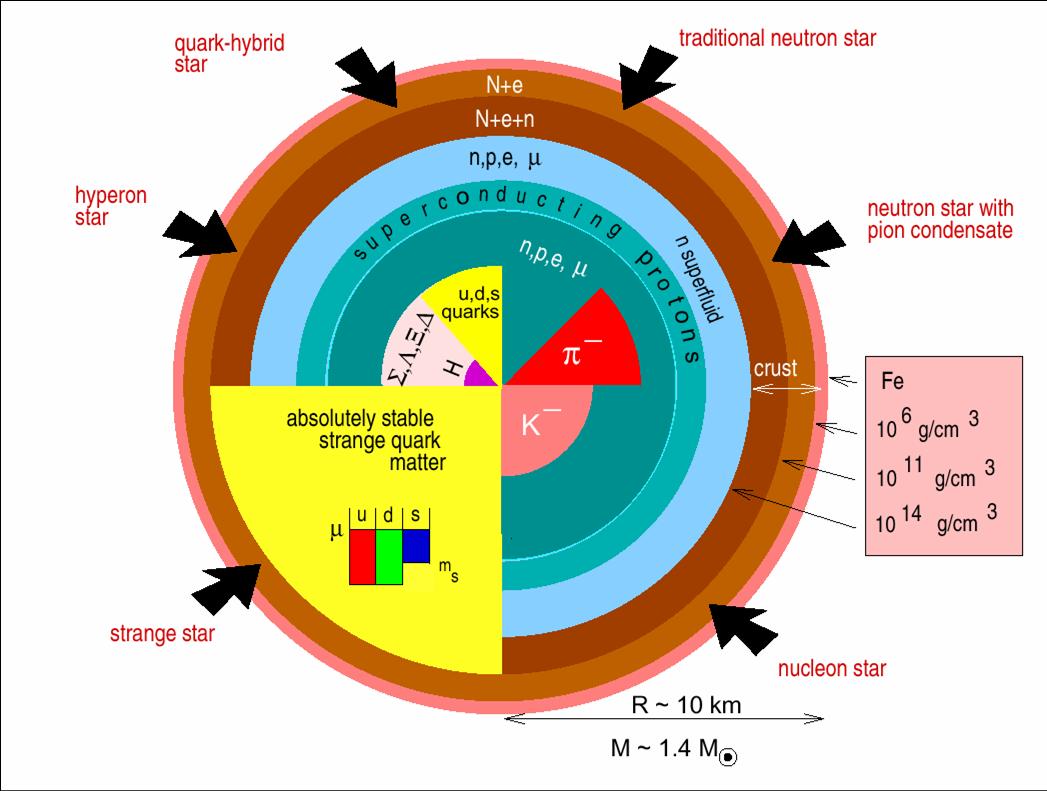
Plusieurs modèles existent sur la composition interne d’une étoile à neutrons.
Coupe d’une étoile à neutrons, du centre vers la surface, pour plusieurs modèles d’étoiles à neutrons, dont le nom associé aux particules « exotiques » qu’on y trouve est signalé en rouge : étoile à nucléons, avec condensat de pions, modèle « traditionnel », avec un noyau de quarks, avec des hypérons, et étoile étrange presque entièrement composée de quarks. Selon les connaissances actuelles sur les interactions régissant les particules de la famille des neutrons (les hadrons), encore incomplètes, plusieurs modèles font intervenir d’autres particules que les neutrons. Ces particules sont très instables dans des milieux de plus faible densité, et on ne les observe que brièvement dans les collisionneurs dédiés à l’étude de la physique des particules élémentaires. Il se pourrait même que les neutrons s’effondrent eux-mêmes en des particules plus élémentaires, les quarks, et forment un mélange de quarks, contenant notamment des quarks dits « étranges » (une des 6 catégories de quarks connues), qui donneraient leur nom d’étoiles à quarks ou étoiles étranges à ces astres assez semblables (du dehors) à des étoiles à neutrons.

La surface des étoiles à neutrons

Notons que si les neutrons constituent la composante essentielle de ces étoiles, c’est seulement dans les parties internes, où les électrons sont maintenus sous l’effet énorme de leur poids. Mais dans les parties externes, on s’attendait à un mélange d’atomes de fer (noyaux très enrichis en neutrons), mêlés à des protons et à des électrons circulant librement, et peut-être à d’autres noyaux atomiques. Puis il fut établi que sous l’effet d’écrasement du fer par la gravité extrême de l’étoile, malgré des températures élevées (estimées aujourd’hui à des centaines de milliers de degrés), le fer serait sous forme solide, cristalline. Donc, cette étoile serait recouverte d’une croûte métallique extrêmement dense et chaude.

La découverte des pulsars et le questionnement sur leur nature

Andrew Cameron émit l’idée, vers 1966, que la petite étoile atypique découverte au cœur de la nébuleuse du Crabe, vestige d’une explosion de supernova, pouvait effectivement être une étoile à neutrons. Mais il ne proposa pas d’en chercher les émissions radio.

Dans les années 1930 et 1940, du temps des premières théories des étoiles à neutrons, la radioastronomie était une science balbutiante, et l’on ne se doutait pas que c’est grâce aux ondes radio que l’on prouverait leur existence. De plus, jusqu’au milieu des années 1960, les spécialistes des étoiles à neutrons s’intéressaient surtout à ce qu’il y avait dedans. Or, la cause de leur rayonnement puissant est liée à ce qu’il y a autour.

En 1967, une étudiante en thèse sous la direction d’Antony Hewish, Jocelyn Bell, découvrait, en cherchant tout autre chose, un signal radio se répétant périodiquement, avec une période de 1,33 seconde. Intriguée, elle fit les tests habituels : cette source, si elle était cosmique, devait réapparaître au même endroit apparent du ciel avec une périodicité d’un jour sidéral, 23 h 56 min, comme les étoiles. Ce fut le cas. Cette source fut nommée CP 1919, car elle se trouvait à une ascension droite de 19 heures et 19 minutes.

Pendant quelques mois, l’équipe ne publia pas cette découverte. Il fallait d’abord proposer des explications.

Un peu par dérision, on appela ce signal « petits hommes verts », comme si c’était les manifestations d’une civilisation extraterrestre. Mais on envisagea plus sérieusement la possibilité de rayonnement associé à une étoile variable pulsante à très courte période (1,33 seconde) : une « pulsating star ». Seul succès de ce modèle, le mot composé « pulsating star » est resté, mais agrégé en un seul mot : « pulsar ». Pour qu’une étoile oscille aussi rapidement, elle devait probablement être très petite.

Il y avait d’autres idées : on pensa (à raison) que ces impulsions pouvaient provenir d’une étoile en rotation rapide qui émettrait continûment des ondes radio dans un faisceau de directions assez restreint, à la manière d’un phare. À chaque tour, lorsque nous passerions dans le faisceau, nous capterions ces ondes radio, et cela donnerait une impulsion. Pour qu’une étoile tourne sur elle-même en 1,33 seconde sans être détruite par les forces centripètes, il fallait qu’elle soit petite. Ce pouvait être une naine blanche… ou une de ces fameuses étoiles à neutrons.

L’article fut publié avec l’énonciation de ces hypothèses [4].

Ce fut un véritable succès. Très rapidement, des astronomes pointèrent leurs radiotélescopes à la recherche d’autres sources. Et bien entendu, ils voulurent vérifier l’hypothèse de Cameron à propos de la nébuleuse du Crabe. Et dans cette région, ils découvrirent une émission pulsée avec une période de seulement 33 millisecondes. En admettant qu’il s’agissait d’un objet tournant, il ne pouvait avoir les dimensions d’une naine blanche (quelques milliers de kilomètres) trop grande pour résister à l’effet centrifuge. Ce devait être un astre plus petit : une étoile à neutrons.

Les radioastronomes, dans la foulée de CP 1919 et du Crabe, détectèrent un pulsar associé à la nébuleuse des Voiles (Vela), qui est également un reste de supernova. Et l’on en découvrit une dizaine d’autres. Aujourd’hui, on en connaît plus de 2 000, et on estime leur nombre dans notre Galaxie à plus de 100 000.

Le Crabe a une période de 33 millisecondes, ce qui correspond à une fréquence d’environ 30 Hz. Vela a une période de 89 ms, soit une fréquence de 11 Hz, et CP 1919 a une période de 1,33 s, soit une fréquence de 0,75 Hz. Il y eut encore des travaux sur des émissions pulsées non liées à la rotation d’une étoile, de plus en plus souvent pour en contester la validité. La grande régularité des pulsations était facilement explicable pour un objet tournant et très massif, mais moins pour des oscillations, dont le spectre de fréquences n’a quasiment jamais une seule fréquence, comme c’était observé, ni la même stabilité.

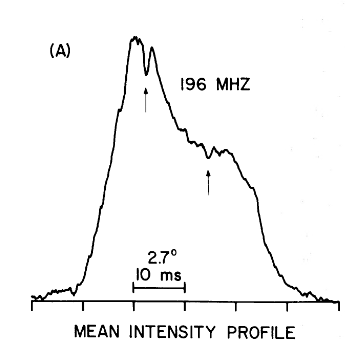
Le profil d’émission radio du pulsar PSR 1919+21, pour une bande de fréquences centrée sur 196 MHz, résulte de la moyenne d’observations sur un ensemble de 1 300 périodes du pulsar. Faire des moyennes de ce type est généralement le seul moyen pour mettre en évidence le profil d’émission d’un pulsar. Cela suppose de connaître à l’avance sa période. C’est pour cela que la découverte de nouveaux pulsars (donc de période inconnue) ne va pas de soi, surtout s’ils nous envoient un signal de faible intensité. Cela demande l’application de méthodes spécifiques d’analyse du signal et des traitements numériques significatifs. (L. J. Cordes, The Astrophysical Journal 195:193-202, 1975)

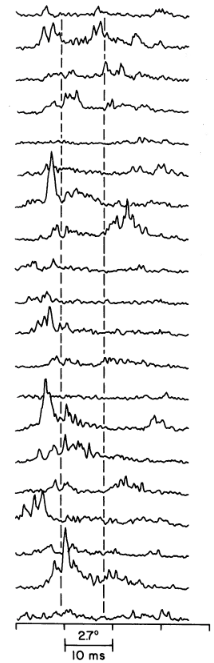
Observation du pulsar PSR 1919+21, découvert par Jocelyn Bell. Le temps est en abscisses, et l’intensité du signal est en ordonnées. Dans cette séquence, les observations à 20 instants différents sont présentées, toutes recalées sur la périodicité de 1,33 seconde du pulsar. Ces observations ont été centrées sur la fréquence de 111,5 MHz. Il est difficile de remarquer la périodicité du signal au premier coup d’œil, d’abord parce que le pulsar, s’il a la régularité d’une horloge, n’émet pas forcément avec la même intensité à chaque période, et d’autre part à cause d’effets de propagation du signal à travers le milieu interstellaire, notamment des effets de scintillation. C’est donc en effectuant une moyenne sur plusieurs périodes que l’on peut faire clairement apparaître la forme du signal d’un pulsar (cf. la figure suivante). (L. J. Cordes, The Astrophysical Journal 195:193-202, 1975)

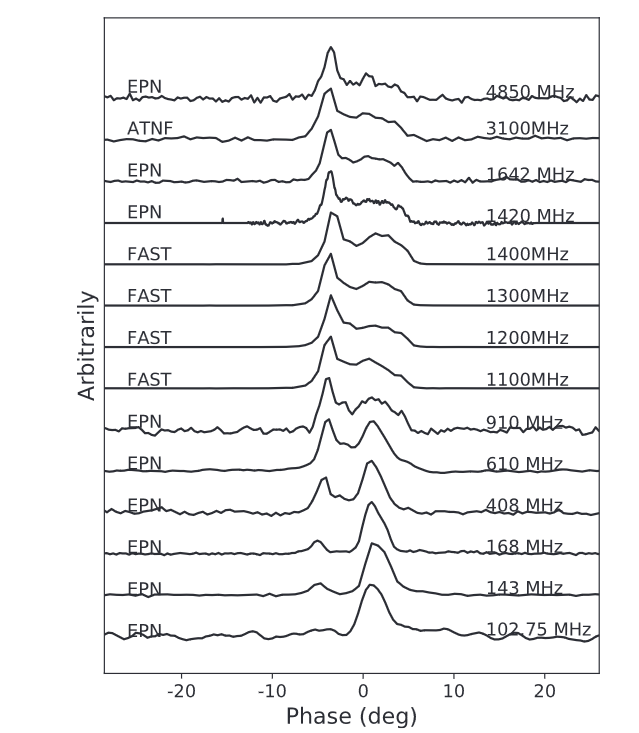
Profil radio moyen du pulsar B1737+13, à différentes fréquences du domaine radio. L’axe horizontal indique le temps divisé par la période du pulsar, et centré au maximum de l’émission. La période est de 0,803 seconde. Seulement 50 % de la période est montrée, car il n’y a pas de signal le reste du temps. L’axe vertical indique l’intensité du rayonnement radio, dans une bande de fréquence centrée sur la valeur indiquée. Ces observations ont été faites avec trois radiotélescopes (chacun d’entre eux ne couvrant pas toutes les fréquences), en Europe, en Australie et en Chine. Ce pulsar est un des rares dont le profil d’émission possède pas moins de 5 maxima d’émission.
(Q. J. Zhi et al., The Astrophysical Journal 926:73, 2022)

Les étoiles à neutrons sortent de l’oubli incrédule

Les radioastronomes étaient frappés par le caractère extrêmement régulier des pulsations. Alors, afin d’en éprouver les limites, ils en firent un chronométrage sur le long terme à l’aide d’horloges atomiques. Et l’on découvrit une variation continue de la période qui consistait en un accroissement  très lent et régulier. Par exemple, chaque seconde, la période du pulsar du Crabe s’accroît de 10^-12 seconde. L’accroissement est analogue pour le pulsar Vela. Mais pour la plupart des autres pulsars alors découverts, dont la période était de l’ordre d’une seconde, la dérive est comprise entre 10^-14 et 10^-16 seconde par seconde. C’est très peu, mais en quelques mois d’observation avec de bonnes horloges, c’était mesurable.

Le physicien italien Pacini, alors aux États-Unis, s’intéressait beaucoup à l’hypothèse des étoiles à neutrons pour expliquer les pulsars. Il remarqua en 1968 que si une étoile géante avec un champ magnétique en surface typique de ce genre d’étoiles s’effondre, alors le champ magnétique est entraîné avec la matière [5]. Plus précisément, le flux magnétique est conservé, c’est-à-dire que le champ magnétique multiplié par la surface de l’étoile est constant. Comme la surface de l’étoile devenait minuscule, le champ magnétique devait être énorme. Pour une étoile à neutrons, il estima un champ de l’ordre de 10^-8 teslas [6]. Quelques mois plus tard, il publiait un autre article reprenant les travaux conduits vers 1950 par un autre astronome, Armin Deutsch, où il était expliqué (calculs à l’appui) qu’une étoile en rotation avec un champ magnétique non aligné (c’est-à-dire que l’axe de symétrie du champ magnétique ne coïncide pas avec l’axe de rotation) se comporte comme une antenne électrique rayonnant à la fréquence correspondant à la rotation de l’étoile. Avec les pulsars, Pacini montrait qu’on avait donc des antennes avec un champ très puissant émettant des ondes à des fréquences de l’ordre de 1 à 100 Hz (par exemple 30 Hz pour le pulsar du Crabe). Il calcula une puissance émise par ces antennes, et il montra qu’elle était compatible avec la puissance perdue avec le ralentissement de la rotation des étoiles, pourvu qu’elles aient les caractéristiques d’une étoile à neutrons. Autrement dit, le rayonnement électromagnétique associé à la rotation des étoiles à neutrons expliquait leur ralentissement progressif.

A ce stade, il était quasiment prouvé que les pulsars observés en ondes radio étaient une manifestation des étoiles à neutrons.

La même année, deux astronomes américains, Peter Goldreich et William Julian, publiaient un article où l’hypothèse de Pacini d’une étoile à neutrons entourée de vide était contestée, sans revenir pour autant sur la validité de ses conclusions. Lorsque de la matière conductrice comme la surface d’une étoile à neutrons ou son éventuelle atmosphère tourne dans un champ magnétique, des champs électriques se développent. C’est un résultat bien connu des spécialistes d’électromagnétisme. Goldreich et Julian calculaient pour les pulsars des champs électriques si forts, que forcément des particules électriquement chargées (comme des électrons ou des ions) doivent être arrachées de l’étoile, formant ainsi un plasma. Ils prouvaient même qu’en l’absence d’atmosphère, les forces électriques auraient été un million de fois plus fortes que la gravitation énorme de l’étoile. Donc, il devait y avoir une atmosphère, et vu la température de l’étoile, elle ne pouvait contenir que de la matière ionisée : électrons, ions et autres particules électriquement chargées. Un gaz composé de matière ionisée est appelé un « plasma ». Ainsi, l’étoile à neutrons était dotée d’un champ magnétique très intense, dans lequel circule un plasma. Un tel environnement a un nom : c’est une « magnétosphère ». Des magnétosphères existent au voisinage de nombreuses planètes, dont la Terre, et d’étoiles [7]. Cependant, la magnétosphère des pulsars a une importante différence avec celle des planètes et des étoiles standard : le plasma qui la constitue n’est pas neutre. Autrement dit, dans un petit volume autour d’une étoile à neutrons, le nombre de charges électriques négatives et le nombre de charges électriques positives sont inégaux. Un calcul simple montrait même quelle devait être la densité de charges électriques résultante près de l’étoile au voisinage des pôles : on atteignait l’équivalent de 10¹² fois la charge d’un électron par centimètre cube. Cela était en cohérence avec l’existence des champs électriques très forts.

Ces travaux et des centaines d’autres qui allaient suivre durant les décennies à venir montraient que l’environnement des étoiles à neutrons est un milieu extrêmement énergétique où des particules, en particulier des électrons, arrachées de l’étoile sont accélérées par des champs électriques de l’ordre de 10¹⁴ volts par mètre, atteignant en quelques centimètres des vitesses comparables à la vitesse de la lumière. On étudia les processus de rayonnement de ces particules, et l’on définit un nouveau concept : le « rayonnement de synchro-courbure » que l’on ne rencontre que là (et peut-être au voisinage de trous noirs). Ce rayonnement est causé par des particules de très haute énergie se propageant le long des lignes de champ magnétique. Ce rayonnement est essentiellement dans la gamme d’énergie des rayons gamma. On chercha donc à détecter les pulsars avec des télescopes gamma. Mais avant même les observations en rayonnement gamma (qui viendront dans les années 2000), l’astrophysicien anglais Peter Sturrock montra en 1971 que chaque photon gamma émis par ces particules, en interagissant avec le champ magnétique très puissant de l’étoile, ou avec d’autres photons, devait se transformer en un électron et un anti-électron, aussi appelé « positon ». La conclusion décevante de son article était donc que les rayonnements gamma des étoiles à neutrons seraient en grande partie absorbés par ces créations de paires d’électrons et de positons, donc pas si faciles à observer. Mais la chose formidable était de constater que quelques électrons arrachés très brutalement à l’étoile par des champs électriques extrêmes émettent des rayonnements gamma qui ensuite se transforment en matière (des électrons et des positons). Ces nouveaux électrons et positons sont à leur tour accélérés, ils rayonnent d’autres rayons gamma, ce qui produit encore d’autres paires d’électrons et de positons.

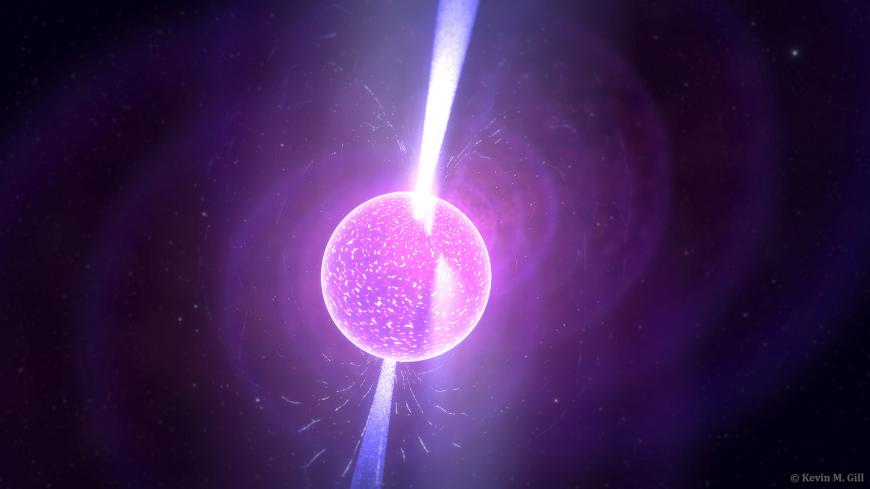
Une étoile à neutrons est un émetteur d’ondes radio. Ces ondes sont émises principalement au voisinage des pôles magnétiques de l’étoile, et dans des directions formant des faisceaux assez étroits. Quand l’étoile tourne, ces faisceaux balayent l’espace, comme le ferait le faisceau d’un phare. Quand nous passons dans le faisceau, nous voyons le signal du pulsar apparaître, et s’éteindre autrement, et cela cause l’aspect pulsé des émissions. Les émissions à d’autres longueurs d’onde (visible, X, gamma) sont également émises dans des faisceaux plus ou moins étroits, et ils montrent également un aspect pulsé périodique.

Des astres morts ?

On estime aujourd’hui qu’un électron (dit « primaire ») arraché à la surface de l’étoile à neutrons produit ainsi environ 100 000 autres électrons et positons (dits « secondaires »).

Normalement, lorsqu’un électron et un positon se rencontrent, ils peuvent s’annihiler et se transformer à nouveau en rayon gamma. C’est ce qu’on appelle la recombinaison. Mais pour que celle-ci ait lieu, il faut que les particules aient le temps d’interagir, car cette opération n’est pas instantanée. Or, dans la magnétosphère des pulsars, les champs électriques très forts accélèrent les électrons et les positons à des vitesses opposées très grandes : tout d’abord, deux particules d’une même paire s’écartent, donc elles ne se recombinent pas. Et d’une manière générale, les positons croisant des électrons allant à des vitesses très différentes, ils se « voient » très brièvement, ils n’ont pas le temps d’interagir, ils ne se recombinent pas.

Ainsi, la magnétosphère d’un pulsar est une véritable source de matière. Une partie retombe sur l’étoile à neutrons (et là, la recombinaison peut se produire), mais une autre partie du plasma est envoyée dans l’espace, constituant un vent formé d’électrons et de positons. Ce vent se propage quasiment à la vitesse de la lumière [8].

De plus, si les rayons gamma produits près de l’étoile sont effectivement absorbés par ce processus, comme prévu par Sturrock, d’autres rayons gamma et X sont produits plus loin, notamment dans ce vent ultra-rapide… Et aujourd’hui, on peut les observer, notamment avec des instruments comme le télescope X Nicer à bord de la Station spatiale internationale, le télescope gamma du satellite Fermi, et les télescopes à effet Tcherenkov.

Si un astre est « vivant » tant qu’il rayonne, il est clair que la « vie » d’une étoile très massive ne cesse pas au moment de la supernova. S’il reste une étoile à neutrons, la « vie » continue. Mais combien de temps ?

Pour répondre à cette question, il faut faire un bilan des puissances rayonnées. Le rayonnement vient principalement de la magnétosphère, et pas de l’étoile. La magnétosphère fonctionne grâce à un champ magnétique très fort et à une rotation rapide de l’étoile. Mais dans l’étoile à neutrons, le champ magnétique n’est pas produit dynamiquement, comme avec une dynamo. C’est un champ magnétique rémanent, comme celui d’un aimant en acier, même si les processus de rémanence, liés à des phénomènes de supraconductivité, sont différents. Donc, petit à petit, ce champ magnétique diminue.

En outre, comme nous l’avons vu, la magnétosphère, en tournant, se comporte comme une antenne émettant une onde à très basse fréquence qui rayonne, c’est-à-dire qu’elle envoie de l’énergie vers l’extérieur, et cela cause le ralentissement progressif de la rotation. Toute la dynamique de la magnétosphère (le rayonnement X et gamma, la création de matière et l’accélération du vent de pulsar) est alimentée en énergie par la rotation de l’étoile.

Ainsi, en quelques millions d’années, le pulsar s’épuise. La champ magnétique devenant trop faible (10⁴ à 10⁶ T), la rotation devenant trop lente (une période de quelques secondes), la machinerie s’éteint. L’étoile à neutrons existe toujours, mais elle n’alimente plus une magnétosphère assez dynamique pour produire un pulsar. Alors, les spécialistes des étoiles à neutrons reprennent à leur compte la notion de « vie d’une étoile » et déclarent la « mort » du pulsar. Pour désigner le domaine de paramètres caractérisant les étoiles à neutrons trop lentes et trop peu magnétisées pour former un pulsar, les astronomes parlent même de « cimetière ».

Cependant, il arrive que cette mort ne soit pas définitive… ce qui est tout de même atypique ! Pourvu qu’un pulsar fasse partie d’un système d’étoiles doubles, il se peut que la compagne, en perdant de la matière qui tombe sur l’étoile à neutrons, ravive l’activité de ce pulsar qu’on croyait mort. On parle alors de pulsars recyclés. On les distingue des pulsars standard, car ils ont un champ magnétique faible (de l’ordre de 10⁴ à 10⁶ T tout de même), mais ils tournent très vite, avec une période typique de 10 millisecondes. Ceux-là peuvent alors être actifs durant des centaines de millions d’années, excédant largement la durée durant laquelle leur étoile progénitrice a brillé dans sa phase d’étoile de la séquence principale puis de géante.

Simulation numérique de l’environnement d’une étoile à neutrons. L’étoile, d’un rayon de l’ordre de 12 km, est représentée par la sphère bleutée. Son environnement comprend un grand nombre d’électrons et de positons qui ont été créés lors d’interactions entre le rayonnement gamma émis par les particules préexistantes de haute énergie et le champ magnétique, ou entre le rayonnement des particules de haute énergie et le rayonnement thermique de l’étoile (rayonnement de corps noir, ici principalement des rayons X). Sur l’image, un pôle magnétique est représenté en bleu vif sur la sphère. Les lignes représentent des trajectoires d’électrons de faible énergie (en bleu) et de positons de faible énergie (en rouge) ainsi que des électrons et positons de haute énergie (en blanc). Ce sont les particules de haute énergie qui émettent des rayons gamma, eux-mêmes capables de créer de nouvelles paires électron-positon. (Gabrielle Brambilla, université de Milan, Italie, et NASA’s Scientific Visualization Studio)

50 ans de physique des pulsars

Voilà plus de cinquante ans, avec la découverte des pulsars à l’aide de radiotélescopes, s’ouvrait un nouveau chapitre de l’astrophysique. Les pulsars sont des objets fantastiques à étudier. Les étoiles à neutrons sont les astres les plus compacts qu’il soit possible d’observer directement. Au-delà, ce sont des trous noirs, dont les observations (ondes gravitationnelles mises à part) sont indirectes. Les conditions physiques régnant dans les pulsars sont extrêmes. En ce sens, ce sont de passionnants laboratoires de physique que l’on ne pourra jamais recréer sur Terre. Mais, en plus d’être intéressants en eux-mêmes, les pulsars sont d’excellents outils pour d’autres études en physique et en cosmologie. En contraignant la relation entre leur masse et leur rayon, on peut en apprendre beaucoup sur les propriétés de la matière subatomique et sur l’interaction forte. De par la régularité des impulsions qu’ils nous envoient, les pulsars sont de merveilleuses horloges disséminées dans notre Galaxie et dans les galaxies voisines. Ce sont ainsi des instruments de mesure extrêmement précieux, dont on peut se servir pour vérifier (ou remettre en cause) les théories de la relativité, pour laquelle la mesure du temps est essentielle, ou pour révéler des systèmes d’astres multiples dont certains sont invisibles, ou encore pour la mesure d’ondes gravitationnelles de très basses fréquences, liées par exemple à la fusion de trous noirs centraux de galaxies.

Bien que leur luminosité dans le domaine des ondes visibles soit faible, une poignée d’étoiles à neutrons sont observables avec des télescopes optiques. C’est le cas du pulsar du Crabe, formé par la récente explosion de son étoile génitrice en 1054, et dont le reste est l’étoile à neutrons située au centre des images à droite. Une série de courtes poses (moins de 1 milliseconde) avec le Kitt Peak Photon Counting Array (KPCA) à l’observatoire de Kitt Peak, accumulées pendant deux heures et mises en phase avec une période de 33,367 ms montrent que l’émission optique (à travers un filtre pour la bande B) de l’étoile à neutrons de la nébuleuse du Crabe varie avec la même période que ses émissions radio, ainsi qu’avec ses émissions en rayons X et gamma.

par Fabrice MOTTEZ | CNRS / Observatoire de Paris-PSL

Publié dans le magazine L’Astronomie Mai 2023

Notes :

1. Cours d’Agnès Acker, Éd. Masson.
2. Prix Nobel de physique 1922.
3. En admettant qu’il existe des astronomes normaux !
4. Cet article valut à Antony Hewish l’obtention du prix Nobel de physique 1974. Malheureusement, sa jeune étudiante, qui avait su saisir l’opportunité de cette découverte inattendue, allant bien au-delà des ambitions de son sujet de thèse initial, et qui avait mené une analyse pertinente de ses observations, n’obtint pas l’honneur de partager cette prestigieuse récompense. La non-attribution du prix à Jocelyn Bell a fréquemment été reprochée au comité Nobel, à juste titre.
5. Sous réserve que sa matière soit un très bon conducteur électrique, ce qui est le cas.
6. C’est 10^12 fois celui de la Terre !
7.  La Terre, Jupiter, Saturne, Uranus, Neptune. Pour les étoiles, on utilise plutôt le terme de couronne.
8. 8. Le facteur de Lorentz, qui est le rapport entre l’énergie totale de la particule et son énergie de masse mc2, atteint ici des sommets de l’ordre de 10^6. C’est énorme.