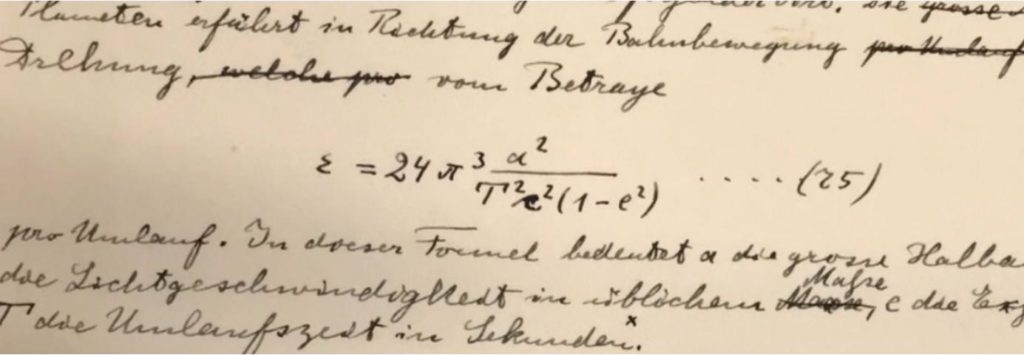Zoom Sur - L'Astronomie Afrique

Des morceaux de Théia enfouis dans le manteau terrestre

par Sylvain Bouley | Juil 12, 2021 | Zoom Sur

Selon une étude récente, des blocs du manteau de Théia, la petite planète qui a sans doute percuté la Terre il y a 4,47 milliards d’années, auraient été incorporés dans le manteau terrestre et seraient à l’origine d’anomalies sismiques observées aujourd’hui par les sismologues.

Vue d’artiste de l’impact géant. © Dana Berry/SwRI

Anomalies de vitesse sismique

Le manteau terrestre est l’enveloppe rocheuse de notre planète qui s’étend de 25 à 2 890 km de profondeur. Pour déterminer sa structure, les géophysiciens utilisent notamment les ondes sismiques qui s’y propagent. En mesurant le temps de parcours entre les épicentres de séismes (où sont générées les ondes sismiques) et les stations sismiques (où elles sont enregistrées), ils construisent des cartes tomographiques, représentant la vitesse des ondes sismiques en chaque point du manteau. Les variations de vitesse d’un endroit à un autre traduisent des changements de température, de composition ou de phase. L’interprétation de ces cartes est en fait assez délicate, car il est très difficile (pour ne pas dire impossible) de séparer les contributions d’origine thermique des contributions d’origine chimique si l’on ne dispose pas de données supplémentaires et indépendantes des vitesses sismiques. Quoi qu’il en soit, ces cartes révèlent la présence à la base du manteau de deux régions, l’une stuée à la verticale de l’Afrique et l’autre sous le Pacifique, appelées LLSVP1, dans lesquelle la vitesse des ondes de cisaillement (les ondes S) diminue de 2 à 3 % par rapport à sa valeur moyenne à ces profondeurs (fig. 1).

1. Zones de faibles vitesses d’ondes de cisaillement (ondes S) observées à la base du manteau. Les cartes tomographiques représentées ici indiquent les anomalies de vitesse sismique (en %) par rapport à une vitesse de référence, et dans quatre plages de profondeurs différentes. Suivant le code de couleur adopté ici, les ondes S se propagent plus rapidement dans les régions apparaissant en bleu, et plus lentement dans les régions apparaissant en rouge. À partir de 2000km de profondeur, on voit progressivement apparaître deux zones de faibles vitesses (les LLSVP), l’une sous le Pacifique et l’autre à la verticale de l‘Afrique. Tous les modèles établis depuis les années 1990 observent ces zones, avec plus ou moins de détails. Certains modèles récents semblent indiquer qu’elles sont plus morcelées que les cartes représentées sur cette figure. (C. Houser et al. – 2008)

Depuis quelques années, les géophysiciens soupçonnent que ces anomalies sont liées à la combinaison de deux phénomènes : une température plus élevée et un changement de composition, sans doute un enrichissement en oxyde de fer (FeO) de quelques pour cent par rapport au reste du manteau. Il existerait ainsi à la base du manteau des régions grandes comme un continent et épaisses de quelques centaines de kilomètres enrichies en fer, et donc légèrement plus denses que les régions voisines. En supposant que cette hypothèse est exacte, le scénario qui a conduit à la formation de ces régions reste, lui, très mal connu. Les hypothèses qui reviennent le plus souvent invoquent des processus liés à la cristallisation de l’océan magmatique, à la subduction d’une croûte primitive, ou encore à la différenciation partielle du manteau. À l’occasion de la 52e Lunar and Planetary Science Conference, qui s’est tenue en mars dernier, une équipe de chercheurs a proposé une nouvelle hypothèse faisant intervenir l’impact géant dont le système Terre-Lune que nous connaissons aujourd’hui serait issu.

Des résidus de Théia cachés au fond du manteau terrestre

Rappelons d’abord que cet impact serait survenu il y a environ 4,47 milliards d’années (Ga), et qu’il aurait détruit l’impacteur (Théia) et excavé une partie du manteau de la proto-Terre . Une partie des débris serait retombée sur la Terre, et le reste utilisé pour former la Lune. Étant donné sa taille, Théia devait elle aussi être différenciée en un manteau et un noyau. L’hypothèse proposée par Qian Yuan et ses collègues est que le manteau de Théia était composé de matériau globalement plus dense que celui du manteau de la proto-Terre et qu’après l’impact, des petits blocs de ce manteau ont été incorporés tels quels dans le nouveau manteau terrestre (fig. 2). Plus lourds, les morceaux de Théia auraient rapidement migré vers la base du manteau terrestre pour former une petite couche de roches enrichies en oxyde de fer. Les mouvements de convection animant le manteau auraient ensuite remodelé cette couche pour lui donner la forme de deux grands massifs de quelques milliers de kilomètres situés aux antipodes l’un de l’autre. Ce scénario repose principalement sur deux éléments. D’une part, des modèles géochimiques de composition du manteau de Théia établis en 2019, et qui suggèrent que ce manteau était un peu plus riche en oxyde de fer (de 2,0 à 3,5 %) que ne l’est le manteau terrestre actuel. Et d’autre part, une série de simulations numériques reproduisant la formation d’une couche de matériau dense autour du noyau à la suite de la migration de petits blocs disposés près de la surface, puis la déformation de cette couche initiale sous l’effet de la convection du manteau, en particulier des courants descendants.

2. Selon le scénario proposé par Qian Yuan et ses collègues, le manteau de Théia (en rouge) était enrichi en fer par rapport au manteau de la proto-Terre (en vert) (A). Après l’impact, des blocs de ce manteau ont été incorporés dans le manteau terrestre (B). Plus lourds, ils ont migré vers la base de celui-ci pour former une couche de roches plus denses que le reste du manteau (C). La convection du manteau a ensuite remodelé cette couche, notamment sous l’action des courants descendants (flèches grises) qui poussent le matériau plus dense sur les côtés (D). Le résultat serait les grandes régions de faible vitesse sismique observées par les sismologues à la base du manteau et appelées LLSVP. (2021, F. Deschamps)

Cette hypothèse est intéressante, mais elle comporte aussi quelques points faibles. Les simulations numériques supposent que les petits blocs issus du manteau de Théia sont restés solides lors de et immédiatement après l’impact, ce qui est loin d’être certain étant donné les énergies et les températures mises en jeu lors de cet événement. Par ailleurs, certains modèles tomographiques récents suggèrent que les régions de faibles vitesses sismiques observées à la base du manteau, les LLSVP, sont plus morcelées que ce qu’on pensait jusqu’à présent, ce qui pourrait signifier qu’elles sont moins volumineuses que prévu et/ou que le matériau qui les compose est moins dense. Dans ces conditions, l’hypothèse qu’elles sont issues de résidus de Théia s’accorde moins bien avec la taille et la composition supposées de Théia.

Pour tester la validité de leur scénario, Qian Yuan et ses collègues proposent de comparer la composition géochimique des roches basaltiques de certaines îles océaniques (comme Hawaï) avec celle de roches issues du manteau lunaire. Les basaltes océaniques (ou basaltes de points chauds) ont été conduits en surface par des panaches (c’est-à-dire, des courants ascendants composés de roches un peu plus chaudes que le milieu environnant) qui trouvent sans doute leur source dans ou au sommet des LLSVP. Quant aux roches issues du manteau lunaire, il faudra retourner sur notre satellite pour en récolter, car les missions Apollo n’en ont pas rapporté. Des roches de ce type pourraient avoir été exhumées lors de gros impacts, comme celui qui est à l’origine du bassin d’Aitken, près du pôle Sud de la Lune. Cette région revêt donc un intérêt scientifique particulier, et c’est l’une des raisons pour lesquelles la Nasa et l’agence spatiale chinoise projettent d’y envoyer des missions automatiques dans les années qui viennent.

Frédéric Deschamps IESAS, Taipei, Taïwan

L’eau de Lune

par Sylvain Bouley | Juil 12, 2021 | Zoom Sur

Du début des années 1990 jusqu’à nos jours, des missions spatiales dédiées à la recherche de preuves de l’existence d’eau sur la Lune se sont succédé, gérées par différentes agences spatiales. Un aperçu de ces tentatives successives est présenté dans cet article qui montre que de nombreuses questions restent en suspens, en particulier en ce qui concerne l’abondance de la glace.

1. Vue oblique du cratère Cabeus observé à 50 km de distance par NAC / Lunar Reconnaissance Orbiter. Le lieu d’impact de LCROSS est dans le cratère en bas et au milieu de l’image. La plupart des ombres dans l’image sont permanentes. (Arizona State U./NASA)

Un peu avant le retour d’échantillons lunaires par l’agence chinoise, la Nasa a annoncé en grande pompe à l’automne 2020 la découverte d’eau sur la Lune. L’annonce concerne deux articles publiés simultanément dans Nature Astronomy : le premier [1] rapporte une détection en infrarouge depuis un spectromètre installé sur l’avion SOFIA (Stratospheric Observatory for Infrared Astronomy) de la Nasa et de l’agence spatiale allemande (DLR) et concerne l’eau contenue dans des minéraux, présente aux basses latitudes. Le second article [2] modélise la surface à partir de données orbitales existantes à haute résolution, et donne une nouvelle estimation des zones où la glace peut s’accumuler dans les régions polaires. Cette coïncidence ne doit rien au hasard : les études s’inscrivent dans un programme à long terme consacré à l’eau lunaire.

Dans les années 1970, l’étude des échantillons Apollo et Luna avait montré qu’ils sont essentiellement anhydres, sans eau libre (H2O) ni terminaison hydroxyle (OH), y compris dans les minéraux hydrophiles tels qu’argiles et amphiboles (silicates apparentés aux pyroxènes mais incluant des terminaisons hydroxyles). Les faibles traces d’eau étaient attribuées à des contaminations lors du voyage de retour dans les capsules Apollo ou lors de l’atterrissage. Il y avait consensus pour dire que non seulement la Lune était dépourvue d’eau en surface (ce qui s’explique par les températures diurnes maximales), mais que son manteau avait toujours été globalement sec.

Les années 1990: les missions Clementine et Lunar Prospector

Paradoxalement, l’histoire moderne de l’eau lunaire commence sur Mercure en 1992. À la surprise générale, le radiotélescope d’Arecibo indique alors la détection de glace d’eau dans les régions polaires de Mercure, dans des fonds de cratères qui restent en permanence à l’abri du Soleil et où la température est perpétuellement très basse, de l’ordre de 100 K, malgré la proximité du Soleil, l’absence d’atmosphère et l’effroyable température diurne. Ces régions constituent des « pièges froids » où l’eau présente en surface a pu s’accumuler sous forme de glace et perdurer pendant des milliards d’années. Cette détection relançait la question de la présence de glace aux pôles de la Lune, modélisée depuis le début des années 1960 et jugée très probable, la température maximum des zones à l’ombre étant tout aussi basse que sur Mercure (fig. 1). Mais les pôles lunaires sont plus difficilement observables depuis la Terre et les observations d’Arecibo restèrent infructueuses.

À l’échelle de temps considérée, les impacts de comètes et d’astéroïdes constituent évidemment un apport d’eau quantitativement important, et d’un intérêt fondamental pour étudier l’origine de l’eau terrestre et la nébuleuse primordiale. Mais il existe deux autres apports potentiels : d’une part, l’eau du manteau qui peut se retrouver comme eau constitutive dans les roches volcaniques sous forme H2O ou hydroxyle OH ; d’autre part, l’implantation de protons (noyaux d’hydrogène) du vent solaire dans le régolithe, a priori concentrés dans les premiers mètres de la surface selon l’efficacité des mécanismes de brassage vertical. Si molécules et radicaux sont remobilisés, ils pourraient migrer en surface et se trouver coincés dans les pièges froids avant de s’échapper de la surface.

En 1994, la Nasa se fait un peu forcer la main par le département de la Défense américine qui souhaite tester des capteurs modernes dans l’espace. C’est l’origine de la mission Clementine, première mission lunaire Nasa depuis Apollo et donc, notamment, la première à embarquer des capteurs numériques [3]. Celle-ci confirme l’existence de zones qui ne voient jamais la lumière du Soleil dans les régions polaires, notamment dans l’hémisphère Sud à cause de la topographie tourmentée du bassin Pôle Sud-Aitken, un des plus grands bassins d’impact connus, dont Clementine venait justement de révéler l’étendue ; ces régions sont parmi les plus froides du Système solaire. La difficulté pour l’étude de leur composition est évidemment d’observer des régions jamais éclairées par le Soleil, ce qui impose de mesurer une émission provenant de la surface (infrarouge thermique, particules, etc.) ou de recourir à des méthodes actives (diverses techniques radar).

Ces régions n’étant de surcroît pas facilement observables depuis la Terre, une expérience de radar est mise au point en utilisant l’antenne grand gain de Clementine comme émetteur et les stations au sol comme récepteurs ; elle conclut dans un premier temps à la présence de glace, comme sur Mercure. Cette interprétation a toutefois été remise en cause lorsque des observations depuis Arecibo ont montré des signatures similaires dans les régions équatoriales, où la présence de glace est exclue – il s’agirait finalement plutôt d’un effet de la rugosité de surface, et la question de la glace lunaire restait ouverte.

2. Estimation de la glace souterraine autour du pôle Sud (latitude > 80°), selon les mesures de neutrons LEND/LRO intégrées durant plusieurs années. (NASA Goddard Space Centre)

La mission suivante, Lunar Prospector (1998-1999), systématise l’étude de la composition, et la recherche d’eau en particulier. Parce qu’ils ne travaillent pas en lumière réfléchie, les spectromètres gamma et neutrons sont tous deux capables d’observer les régions qui restent en permanence à l’ombre. Les neutrons détectés sont produits par des rayons cosmiques frappant la surface. Le spectromètre à neutrons différenciait neutrons épithermiques (rapides) et thermiques (ralentis par une collision avec H) et permettait donc d’évaluer le nombre d’atomes d’hydrogène en surface avec une très bonne précision (0,01 % en volume). Le spectromètre gamma confirmait la détection des neutrons épithermiques. La méthode est sensible jusqu’à des profondeurs de l’ordre du mètre. La cartographie (à basse résolution) montre des maxima d’hydrogène dans les régions polaires, notamment au Sud, mais aussi des enrichissements locaux dans les régions équatoriales. Les premiers correspondent à la glace d’eau piégée dans les régions perpétuellement à l’ombre (fig. 2), les seconds à l’implantation de protons du vent solaire dans le régolithe lunaire, éventuellement enfouis dans les premiers mètres.

La mission Lunar Prospector se termine par un crash volontaire au fond du cratère Shoemaker, une de ces régions jamais illuminées près du pôle Sud (fig. 3,). Le panache soulevé, observé depuis la Terre, aurait pu permettre d’observer les quantités d’eau stockées là, mais aucune signature n’a été observée. Outre la détection indirecte de glaces polaires, Lunar Prospector a bien mis en évidence la présence d’hydrogène aux basses latitudes, mais sous une forme inconnue.

3. Carte de l’abondance en eau dérivée de l’hydrogène, selon les mesures de neutrons LRO. Les flèches désignent les régions où la quantité d’hydrogène est maximale ; 1S est le site d’impact de LCROSS, 2S celui de Lunar Prospector.

Les années 2000: un nouveau départ

Une dizaine d’années plus tard, la Lune redevient à la mode auprès des agences spatiales. Les missions européenne Smart-1 (2003-2006) puis japonaise Kaguya (2007-2009) refont une cartographie précise avant d’être précipitées en surface, tandis que la mission indienne Chandrayaan-1 (2008-2009) embarque le premier spectroimageur couvrant les signatures infrarouges d’OH et H2O (M3) ainsi qu’une petite sonde d’impact lancée dans le cratère Shackleton, au plus près du pôle Sud. Aucun de ces impacts n’a permis de détecter l’eau attendue.

Les deux missions américaines Lunar Reconnaissance Orbiter (LRO) et LCROSS sont lancées simultanément en octobre 2009. LCROSS est entièrement tournée vers la recherche d’eau et reprend en grand l’expérience d’impact de Lunar Prospector : c’est cette fois l’étage de propulsion Centaur qui est précipité vers une zone d’ombre (le cratère Cabeus) (fig. 4), le panache étant observé par la sonde elle-même qui le traverse en suivant le Centaur avec 4 minutes de retard. Les télescopes terrestres, ainsi que Hubble et la sonde LRO observent eux aussi le panache à la recherche de signatures d’eau, de composés organiques et de produits de décomposition.

4. Luminosité totale du panache de l’impact LCROSS mesurée par la sonde de suivi en visible (vert) et en infrarouge (rouge). L’analyse des signatures spectrales montre la présence de vapeur d’eau et de glace pour un total de 5,6 %.

Le panache a été bien moins important et lumineux que prévu, mais des détections ont bel et bien été rapportées par la suite, avec une abondance d’H2O de l’ordre de 5 % en masse pour cette région particulière – la seule détection nette à la suite d’un impact, et pendant longtemps le plus solide indice de la présence de glace H2O en surface. Le radar de Chandrayaan-1 a montré ensuite que Cabeus est en fait pauvre en glace comparé à d’autres cratères de la région. Il a également mis en évidence 40 sites plongés dans l’ombre en permanence dans les régions polaires Nord, qui correspondent potentiellement aux quantités de glaces inférées des mesures de neutrons de Lunar Prospector.

5. Ombres en surface à différentes échelles: a) Vue oblique du cratère Cabeus observé à 50 km de distance par Lunar Reconnaissance Orbiter / NAC ; b) Image du rover Chang’e-3 / Yutu ; c) Image Apollo 14 du régolithe lunaire. (Hayne et al 2020, Fig 1 – 10.1038/s41550-020-1198-9)

LRO, qui est toujours opérationnelle, a par ailleurs fourni d’importantes contraintes sur la présence d’hydrogène et sur les conditions thermiques à la surface. Son spectromètre UV Lyman alpha et son lidar indiquent également des signatures probables de glace dans des zones d’ombre permanente. L’article récent de Paul Hayne et de son équipe utilise les images et les modèles numériques de terrain produits par LRO pour modéliser la surface à très haute résolution et identifier les zones en permanence à l’ombre jusqu’à des tailles inférieures au centimètre (fig. 5). Dans un second temps, il utilise les observations du radiomètre pour déterminer lesquels peuvent effectivement fonctionner comme des pièges froids – ils sont en fait tous situés à des latitudes supérieures à 80°. Ce travail montre qu’en dehors des grands cratères des régions polaires, la glace peut se maintenir dans des niches d’une taille de 10 centimètres, alors que les niches plus petites, bien qu’instables, peuvent constituer des abris temporaires et influer sur le transport d’eau en sur- face (fig. 6).

6. Profondeur de stabilité de la glace autour du pôle Sud (latitude > 80°), modélisée sur la base des observations Diviner / LRO. Les zones en blanc sont des pièges froids où la glace est stable en surface. (Paige et al. 2010, fig 1D – 10.1126/science.1187726)

La première détection d’eau dans les minéraux (en fait OH ou H2O) est généralement attribuée à l’instrument M3 sur Chandrayaan-1. Celle-ci a été rapportée en octobre 2009, accompagnée de confirmations par d’autres spectromètres en infrarouge sur les missions Cassini (Nasa/Esa/Asi) et Deep Impact (Nasa) obtenues durant des survols de la Lune. Cette méthode ne détecte la composition que dans la couche superficielle, de l’ordre du micron, et bien sûr dans des régions illuminées. Au-delà de la simple confirmation, les détections par Cassini et Deep Impact apportent une validation fondamentale à la cartographie de la surface par M3 (fig. 7) : celui-ci, dédié aux minéraux volcaniques, ne couvrait qu’en partie la signature OH-H2O à 3 μm et utilisait donc un paramètre spectral indirect. Les instruments de Cassini et Deep Impact, destinés au système de Saturne et à une comète, étaient optimisés pour les glaces ; ils couvraient ce domaine spectral sans la moindre ambiguïté et permettaient de relier le paramètre mesuré par M3 à une quantité d’eau.

7. Carte d’hydratation des sols dérivée des observations M3, et estimation du contenu en eau (projetée sur l’altimétrie LOLA/LRO). Les régions sans détection sont en gris, les sites d’atterrissage Apollo sont signalés en jaune. (Li & Miliken 2017 – 10.1126/sciadv.1701471)

Que sait-on aujourd’hui ?

Les analyses convergent vers une concentration d’eau de 10 à 1 000 ppm (parties par million) avec des maxima aux hautes latitudes et près du terminateur, mais aussi dans certains cratères récents des highlands lunaires. Cela représente environ un verre d’eau par terrain de football, selon l’unité qui devient commune chez les planétologues américains. Bien qu’il soit impossible de distinguer par cette méthode
OH et H2O, il s’agit dans tous les cas d’eau ou d’hydroxyles adsorbés ou constitutifs 8 dans les minéraux: l’eau libre ou faiblement liée n’est pas stable en deçà des hautes latitudes, car elle est rapidement photodissociée. Le maximum près du terminateur et l’absence de corrélation avec l’hydrogène des détecteurs à neutrons laissent penser que ces espèces se déplacent sous l’effet du réchauffement, un mécanisme proposé dès le début des années 1960 et qui pourrait alimenter les pièges froids. Les variations diurnes observées par Deep Impact semblent indiquer une origine liée aux protons du vent solaire.

8. Absorption à 3 μm à proximité du cratère Dufay, mesurée par M3 juste avant midi. La zone encerclée est anormalement claire et hydratée mais de même composition que le voisinage. Elle pourrait résulter d’un impact de comète dans certaines conditions. (Wöhler et al 2019 – 10.1051/0004-6361/201935927)

Des analyses plus récentes des mesures M3 ont montré quelques maxima d’absorption locaux aux basses latitudes plus marqués que dans les régions polaires, notamment une région qui pourrait correspondre à un impact relativement récent de météorite ou de comète (fig. 8). Une autre réanalyse très minutieuse des observations M3 a porté sur des régions polaires illuminées indirectement par réflexion sur les parois de cratères, et donc très peu chauffées. Elle a confirmé des signatures de glace, corrélées à celles fournies par les instruments de LRO. La plupart de ces sites correspondent bien à des températures maximales très basses et sont donc des pièges froids, mais ils ne représentent qu’une proportion restreinte des pièges froids actuels. Cela recoupe une hypothèse précédemment formulée selon laquelle l’axe de rotation de la Lune aurait légèrement basculé à une date inconnue, ce qui aurait entraîné la sublimation d’une partie de la glace piégée depuis la formation de la surface. Le fait que les pièges froids apparus après ce basculement ne soient pas remplis suggère que la glace polaire a été mise en place en des temps anciens et ne s’accumule plus de façon significative depuis longtemps.

Parallèlement à ces observations orbitales, de nouvelles analyses de certains échantillons Apollo ont finalement montré en 2008-2011 la présence de traces d’H2O et OH dans des basaltes et des verres pyroclastiques (d’origine volcanique), au-delà de contaminations accidentelles. Cela implique la présence d’eau dans les magmas lunaires, ce qui modifie profondément la compréhension des mécanismes volcaniques, et suggère une source interne pour l’eau observée en surface. Ce mécanisme, ainsi que l’implantation de protons du vent solaire couvrent largement les quantités d’OH et H2O estimées en surface. L’apport des astéroïdes et comètes est beaucoup plus difficile à évaluer, tant il dépend des populations d’impacteurs, des conditions de collision et des phénomènes d’échappement qui suivent de tels événements. Il semble néanmoins couvrir lui aussi les observations, et devrait s’accompagner d’autres composés volatils (organiques) qui pourraient pareillement s’accumuler dans les régions polaires.

Les trois instruments mis en œuvre en 2009 dans la détection d’eau sont des spectromètres en proche infrarouge couvrant la bande à 3μm de l’eau–il s’agit en fait de l’association de deux bandes de vibration OH et d’une bande H2O moins marquée et compliquée par une émission thermique très variable. Impossible dans ces conditions de distinguer OH d’H2O.

9. Image du cratère Clavius sur la carte composite UV-Vis Clementine. Le contour représente la fente du spectromètre de SOFIA. (Hanniball et al 2020, Fig Ext 6b – 10.1038/s41550-020-01222-x)

Les mesures récentes de SOFIA (fig. 9, p. 35) concernent quant à elles la bande à 6 μm d’H2O et sont sans ambiguïté, car il n’y a pas de bande d’OH à proximité. Cependant, elles sont pour l’instant limitées à deux régions de la Lune. Les signatures observées sont similaires à celles de minéraux ou de météorites hydratés, et correspondent à des concentrations dans les verres lunaires de 100 à 400 ppm en masse, soit quatre fois plus que les échantillons Apollo les plus hydratés. L’interprétation proposée est que l’eau est piégée dans des sphérules de verre créées lors d’impacts de micrométéorites ; l’eau elle-même peut être apportée par les micrométéorites, mais la comparaison avec les résultats de la mission américaine LADEE dédiée à l’exosphère lunaire indique qu’elle est plus probablement créée lors du choc, à partir des hydroxyles présents dans le régolithe.

En conclusion

Comme on le voit, c’est l’appariement d’un nombre impressionnant de techniques diverses qui permet de comprendre le puzzle de l’eau lunaire. De nombreuses questions restent en suspens, par exemple en ce qui concerne l’âge et l’abondance de la glace des hautes latitudes (fig. 10). La capacité des pièges froids est plus grande qu’on ne le pensait initialement et représenterait 0,15 % de la surface lunaire – mais personne n’avance de quantité de glace totale à ce stade, d’autant qu’elle pourrait être en partie recouverte de plusieurs mètres de régolithe et demeurer indétectable avec les méthodes utilisées jusqu’à présent. D’un point de vue pratique, l’existence de glace distribuée aux hautes latitudes et relativement facile d’accès pourrait avoir un effet majeur sur les missions habitées en pourvoyant aux besoins de consommation et de construction sur la Lune, et en servant de relais pour des missions plus lointaines.

10. Carte des détections possibles de glace au pôle Sud (latitude > 80°) par M3 sur Chandrayaan-1, en éclairement indirect. Chaque point bleu correspond à un pixel M3 (280m de côté). Les candidats sont filtrés selon les observations de LOLA, LAMP et Diviner (sur LRO). (Li et al 2018 – 10.1073/pnas.1802345115)

Stéphane ERARD | Observatoire de Paris

Une influenceuse, la Lune?

par Sylvain Bouley | Juil 12, 2021 | Zoom Sur

On accorde beaucoup de « pouvoirs » à notre satellite naturel, la Lune. Il existe des effets lunaires réels, liés à sa luminosité ou aux marées qu’elle provoque. Ainsi, les proies se cachent les nuits de pleine Lune, car les prédateurs pourraient les voir, et divers animaux marins, comme le ver palolo, ont des cycles reproductifs liés aux marées pour augmenter les chances d’avoir des descendants. Par contre, il existe aussi de nombreux effets imaginaires, des légendes urbaines parfois démontées depuis longtemps mais qui circulent encore, comme des naissances présumées plus nombreuses lors de la pleine Lune… Deux articles récents ont fait le buzz à ce sujet – mais que racontent-ils vraiment ?

Solomon, Simeon; The Moon and Sleep; Tate; http://www.artuk.org/artworks/the-moon-and-sleep-201934

LE SOMMEIL

Lorsque la Lune éclaire la nuit, il paraît bien normal qu’elle agisse sur le sommeil. On dort effectivement mieux sans lumière et la présence de lumière peut aussi favoriser la tenue d’activités nocturnes. La première étude parue en 2021 (Casiraghi et al., Science Advances 7 no 5, 2021) a demandé aux habitants de 3 villages argentins de noter pendant environ 3 mois quand ils se couchaient et se levaient. Les villages étaient différents : un très rural, sans accès à l’électricité, un très urbanisé (et éclairé), et un troisième en situation intermédiaire. Les mesures montrent des résultats fort dispersés, mais les moyennes indiquent que les habitants du village rural allaient se coucher 25minutes plus tard dans les journées qui précèdent la pleine Lune (et leur sommeil en était d’autant plus court). Le changement est bien moindre pour les urbains, qui ont accès à un éclairage quand ils le veulent. Une discussion avec les ruraux a d’ailleurs confirmé l’effet direct de la lumière lunaire : traditionnellement, les activités continuent en soirée sous Lune gibbeuse ou pleine.

La suite de l’article est moins claire. Une étude de 463 étudiants de l’université de Washington a été menée, mais ils n’étaient suivis qu’une à trois semaines. Il est difficile de savoir si la présence de lumière a pu influencer leur sommeil (dormaient-ils dans des chambres hermétiques ou avec des tentures laissant filtrer la lumière ?), mais aussi si les échantillons d’étudiants étaient comparables – une précision importante puisqu’on compare le sommeil d’étudiants différents selon les phases ! Cette question de l’échantillonnage avait déjà posé problème lors d’une étude médiatisée en 2013 – remesuré sur des échantillons larges et comparables, l’effet revendiqué alors disparaissait… Enfin, curieusement, les auteurs de l’étude récente finissent par évacuer l’effet de la lumière, pourtant clairement identifié : ils favorisent un effet gravifique, lié aux marées, mais en oubliant certains détails qui contredisent directement cette idée.

Raja Ravi Varma, Dame au clair de Lune (1889)

LES CYCLES MENSTRUELS

Un second article dans le même numéro de Science Advances (Helfrich-Förster et al.) se penche sur les règles des femmes. Il analyse les agendas où 22 femmes ont noté pendant 5 à 32 ans les dates de début de leurs règles. Les auteurs définissent une « synchronisation » lunaire comme une suite d’au moins 3 débuts de règles coïncidant avec la pleine Lune ou avec la nouvelle Lune. Sur les 22 femmes étudiées, 10 ne montrent jamais (!) de synchronisation. Les autres présentent des synchronisations uniquement intermittentes et parfois ciblées sur la pleine Lune, parfois sur la nouvelle Lune ! Il n’y a en outre aucun effet généralisé (une femme peut être synchronisée à un moment sans que les autres femmes le soient). Enfin, pour une même femme, le degré de synchronisation peut rester stable, augmenter ou diminuer avec l’âge. Comment dans une telle situation parler d’effet lunaire avéré ? C’est pourtant ce que n’hésitent pas à faire les auteurs en parlant, après avoir mentionné leurs résultats réels, de « haute synchronicité avec la Lune » ou d’une « suggestion forte d’une influence [lunaire] sur les cycles reproducteurs humains »…

Outre des contradictions entre leurs résultats et leurs conclusions, il y a aussi des erreurs : par exemple, ils écrivent que seulement deux sujets (#8 et #11) ne présentent aucune synchronisation, alors qu’il y en a 10 dans la table qu’ils publient. Ils effectuent en outre un test de diverses périodes entre 27 et 32 jours, assurant que seule celle de 29,5 jours donne des résultats significatifs, mais assénant un peu plus loin que les périodes sidérale et anomalistique, pile dans l’intervalle testé, fonctionnent tout aussi bien… Ayant considéré deux phases (PL et NL), les auteurs sont aussi fort embêtés de trouver que cela « marche » avec les deux – une analyse précédente (sur laquelle ils se basent et dont on pourrait aussi longuement discuter) mentionnait en effet juste la pleine Lune. Ils expliquent cela par des époques différentes, les cycles menstruels étant perturbés par la pollution lumineuse qui a fortement augmenté avec le temps. Or, il y a un recouvrement dans les années étudiées par les deux études, et les auteurs ne montrent aucun effet temporel. Si leur hypothèse était correcte, ils devraient pourtant observer une évolution au cours du temps (synchronisation avec uniquement la pleine Lune au début, puis progressivement une synchronisation double, avec la nouvelle Lune et la pleine Lune). On pourrait aussi leur reprocher une sélection importante des références : aucune référence ayant conclu à l’absence d’effet lunaire ne s’y trouve, par exemple, ce qui leur permet de pointer du doigt ces méchants scientifiques « sceptiques des rapports sur l’influence lunaire ». Et quand ils citent les cycles des autres primates, seuls ceux proches de 30 jours sont mentionnés – évacués, les chimpanzés et bonobos (les cycles chez les primates ont des durées entre 11 et 55 jours, ce qui est peu lunaire a priori)… Il est d’ailleurs aussi amusant de voir comme perspective l’utilisation des données des applications de smartphones pour étudier plus avant l’effet « détecté » : cela a déjà été fait par l’application Clue, avec des résultats… négatifs ! Finalement, ils identifient la cause de cette « forte synchronicité » comme étant la gravité via les marées, de nouveau. Ils proposent que les humains soient capables de sentir les changements de pression atmosphérique liés aux marées ou les oscillations de champs électro- magnétiques générées par des perturbations de la magnétoqueue. Faut-il vraiment préciser que ces capacités de détection n’ont jamais été

Yaël Nazé, Université de Liège

Au coeur des galaxies actives ou comment les nuages moléculaires tombent dans le trou noir central

par Sylvain Bouley | Avr 10, 2021 | Zoom Sur

Chaque galaxie possède un trou noir supermassif en son centre, de masse proportionnelle à la masse de son bulbe. Ce sont les galaxies elliptiques, presque toutes en bulbe, qui possèdent les trous noirs les plus massifs, jusqu’à 10 milliards de masses solaires. Par contre, les spirales, aux bulbes plus petits, comme la Voie lactée, abritent des trous noirs plus modestes de 4 millions de masses solaires. Lorsque le trou noir central avale de la matière, provenant du gaz environnant, le noyau de la galaxie devient un noyau actif ou AGN.

Fig. 1. La galaxie spirale barrée NGC 1433 est une galaxie de Seyfert de type 2. Elle est vue ici sur une image HST dans les longueurs d’onde visibles, montrant le centre de la barre (plus jaune) avec les traînées de poussière sombres entourant l’anneau de résonance de Lindblad, où le gaz forme des étoiles jeunes, qui donnent la couleur bleue à l’anneau. La région centrale est agrandie en haut à droite, et l’image HST est en bleu, avec l’image du gaz moléculaire avec ALMA en orange. Le gaz moléculaire révèle un deuxième anneau résonnant à l’intérieur du premier. (D’après Combes et al, 2013)

Les manifestations de cette activité représentent parfois une énorme énergie, lorsque le trou noir central est massif et bien nourri : c’est le phénomène de quasar, où le noyau quasi ponctuel (quasi-star) peut rayonner mille fois plus que la totalité des 200 milliards d’étoiles que contient sa galaxie. Mais le phénomène de quasar est rare, et les AGN qui nous entourent sont en général moins massifs et moins nourris. Ce sont essentiellement des galaxies de Seyfert, dont l’activité du noyau n’empêche pas de voir les étoiles : sa luminosité est comparable ou inférieure à celle de sa galaxie hôte.

Pour une masse de trou noir donnée, il existe une luminosité maximum que ne peut dépasser le noyau actif, quelle que soit la nourriture disponible dans son environnement immédiat : la luminosité d’Eddington. Lorsque le trou noir essaie d’avaler trop de matière, le rayonnement résultant est si intense que la pression de radiation compense et dépasse la gravité, et le gaz est éjecté au lieu d’alimenter le trou noir (voir l’éclairage du numéro 139 de juin 2020). Dès que la luminosité du noyau actif dépasse un centième de cette limite, un vent de matière est éjecté, c’est le phénomène de rétroaction du noyau actif ; le gaz qui aurait dû alimenter le noyau reflue violemment vers l’extérieur,entraînant du gaz moléculaire du disque de la galaxie et empêchant une partie de la formation d’étoiles.

Pour mieux appréhender ces phénomènes, et comprendre comment le trou noir est alimenté, nous avons observé, ces dernières années, une dizaine de galaxies de Seyfert proches avec l’interféromètre ALMA (Atacama Large Millimeter Array). Le réseau comprend 54 antennes de 12 m de diamètre, et la distance maximale entre les antennes atteint 16 km, ce qui permet une résolution spatiale remarquable, jusqu’à 0,010 seconde d’arc (10 mas), soit dix fois mieux que le télescope spatial Hubble (HST) en lumière visible. Dans les longueurs d’onde millimétriques, et même submillimétriques, nous observons les raies de rotation de la molécule CO, la plus abondante après l’hydrogène moléculaire H2 (qui, elle, ne rayonne pas dans ce domaine).

C’est la première fois que l’on peut observer le gaz moléculaire si près du trou noir des noyaux actifs, avec une résolution de quelques années-lumière, qui permet d’entrer dans la sphère d’influence gravitationnelle du trou noir, dont le rayon est typiquement de 10 pc (soit 30 années-lumière). Nous avons pu enfin étudier la dynamique du gaz dans ces régions très proches du centre, et tenter d’élucider la question principale de l’alimentation des trous noirs : comment le gaz qui, en arrivant tout près du noyau, est animé d’une grande rotation peut-il perdre son moment cinétique de rotation et tomber si vite sur le trou noir ?

Une des premières galaxies de Seyfert observées fut la galaxie spirale barrée NGC 1433 (fig. 1). La barre est une perturbation dans le disque de la galaxie qui crée des couples de torsion et permet d’apporter le gaz vers le centre. Mais souvent, il s’arrête à la résonance de Lindblad, pour former un anneau. Le gaz accumulé forme beaucoup d’étoiles, et l’anneau est très brillant, comme le montre l’image HST. La distribution de gaz moléculaire fut une surprise :iln’estpasseulementcondensé dans l’anneau résonnant, mais il s’accumule dans un deuxième anneau plus interne au premier et ne se dirige pas vers le centre. Nos calculs ont pu montrer qu’il existait une deuxième résonance de Lindblad plus près du centre, qui retenait le gaz et l’empêchait de tomber vers le trou noir. L’alimentation du trou noir est intermittente et doit attendre que les couples de torsion aient le bon signe pour faire tomber le gaz. Le changement de signe intervient lorsque la distribution de matière est assez concentrée, et le flot de gaz vers l’anneau contribue à cette concentration.

Dans la galaxie barrée NGC 1566 (fig. 2), cette concentration s’est déjà produite, et nous avons eu la surprise de voir que le gaz moléculaire se distribuait dans une structure spirale nucléaire, avec le même sens d’enroulement que la spirale externe. Cette structure spirale nucléaire n’avait pas été soupçonnée auparavant par manque de résolution spatiale.

Fig. 2 : La galaxie spirale barrée NGC 1566 est une galaxie de Seyfert de type 1. L’image optique à gauche montre le champ de vue d’ALMA (carré rouge) de 18 secondes d’arc de côté (à la longueur d’inde de 0,86mm de la raie CO(3-2)). L’agrandissement à gauche révèle la carte du gaz moléculaire en CO(3-2), et la spirale nucléaire, qui s’enroule dans le même sens que la spirale du disque à grande-échelle. D’après Combes et al (2014).

Sans l’influence du trou noir, les modèles dynamiques prévoient une spirale en sens inverse, ce qui change le signe des couples de torsion dus à la barre. Mais grâce à la concentration de matière, le gaz se condense dans la zone sous influence gravitationnelle du trou noir. La fréquence de rotation du gaz en est considérablement augmentée, car le trou noir impose un potentiel de Kepler. En quelque sorte, dès que le gaz entre dans la sphère d’influence du trou noir, il perd rapidement son moment cinétique de rotation, sous l’influence combinée de la barre et de la spirale nucléaires. Une fois calculé le couple de torsion à partir des observations, nous avons pu quantifier que le gaz allait tomber au centre en deux rotations, soit en 6 millions d’années.

Cette configuration se retrouve dans environ le tiers des galaxies observées, avec des échelles un peu différentes. La figure 3 montre le cas de NGC 1808, une galaxie spirale barrée à flambée de formation stellaire, au centre de laquelle se trouve un anneau formant beaucoup d’étoiles. Là encore, le gaz moléculaire révèle une spirale nucléaire à deux bras, de taille un peu supérieure, sur laquelle la barre va exercer des couples de torsion

qui vont amener le gaz au centre en 60 millions d’années. Le gaz moléculaire est assez dense dans ces régions (au moins 10 millions de particules par cm3) pour que l’émission de la raie de rotation J=4–3 des traceurs de densité HCN et HCO+ puisse être détectée (fig. 3).

Fig. 3 : La galaxie spirale barrée NGC 1808 est une galaxie à flambée de formation d’étoiles. L’image optique à droite montre un centre très brillant, qui abrite aussi un noyau actif. A l’intérieur de l’anneau résonnant de Lindblad, se trouve une spirale nucléaire très contrastée, à la fois dans la raie de CO(3-2), mais aussi HCN(4-3) et HCO+(4-3). Cette configuration permet de calculer à quelle vitesse le gaz va tomber sur le trou noir. D’après Audibert et al (2020).

Les galaxies de Seyfert et plus généralement tous les AGN nous apparaissent sous deux grandes catégories, appelées type 1 et 2. Les AGN de type 1 possèdent des raies très larges, typiquement 20000 km/s, émises par le gaz dans le disque d’accrétion en rotation autour du trou noir. Dans les AGN de type 2, ces raies très larges sont absentes, et n’apparaissent que des raies plus étroites, provenant du gaz plus éloigné du trou noir. Ces deux catégories sont soupçonnées de provenir des mêmes types de noyaux actifs, qui nous apparaissent différemment uniquement par des effets de projection. L’absence de raies larges ne serait pas intrinsèque, mais due à l’obscuration du disque d’accrétion par de la poussière. Dans ce modèle d’unification des AGN, proposé il y a plus de 25 ans, il existe un tore de poussière, assez épais pour absorber la lumière du disque d’accrétion, pour un grand nombre de lignes de visée. Il s’agit d’un tore (comme un donut ou beignet), car au centre, près du trou noir, la poussière est sublimée par les hautes températures. Ce n’est que très récemment que l’on a pu commencer à tester l’existence du tore de poussière. Grâce à la haute résolution spatiale obtenue en infrarouge moyen avec l’interféromètre du VLT (Very Large Telescope de l’ESO), on s’est aperçu que, très fréquemment, la poussière n’était pas alignée comme un tore autour du disque d’accrétion, mais au contraire était disposée de façon perpendiculaire, et semblait emportée avec le reflux de gaz, éjecté par la rétroaction de l’AGN. Ce résultat semble ébranler le paradigme du tore de poussière, mais qu’en est-il du gaz moléculaire au voisinage du trou noir ?

Nos observations ALMA ont permis d’apporter des réponses à cette question. Dans près de 90 % des cas, nous avons découvert au voisinage du trou noir, dans un rayon de l’ordre de 30 années-lumière, un disque de gaz moléculaire, découplé du reste du disque de la galaxie. Nous appelons ce disque circum-nucléaire le tore moléculaire. C’est un disque mince, mais qui doit lui aussi comporter une déficience de molécules au centre, étant donné le rayonnement intense de l’AGN qui doit photodissocier les molécules. Le tore moléculaire est découplé du reste du disque, n’ayant pas la même orientation ni la même cinématique. Lorsqu’il existe une spirale nucléaire, le tore moléculaire se situe à l’intérieur de la spirale. Un exemple est donné sur la figure 4, pour la galaxie spirale barrée NGC 613.

Fig. 4 : La galaxie spirale barrée NGC 613, dont l’image en bas est obtenue avec le VLT de l’ESO, est une galaxie de Seyfert. Le centre a été cartographié en CO(3-2) avec ALMA et l’image en haut à gauche montre les 10 secondes d’arc centrales. Le gaz moléculaire s’accumule dans l’anneau résonnant de Lindblad, puis à l’intérieur se trouve une spirale nucléaire. Le panneau du milieu montre la carte des vitesses du gaz, à la même échelle (rouge vitesses de récession positives, bleu vitesses d’approche). Le panneau de droite est un agrandissement d’un facteur 10 (champ d’une seconde d’arc). Les contours montrent la spirale de gaz moléculaire, et au centre les couleurs représentent l’intensité du continuum (poussière et noyau actif). La figure en haut à droite révèle le gaz dense en HCO+(4-3) : il est disposé en un tore moléculaire, de même taille que le continuum, à l’intérieur de la spirale nucléaire. Le cadre du haut montre le champ de vitesses correspondant : l’orientation du gradient de vitesse est différente de celle du gradient de vitesse à plus grande échelle. Le tore moléculaire est découplé du reste du disque. D’après Combes et al (2019).

Finalement, le tore moléculaire peut en partie rendre compte de l’obscuration nécessaire au modèle d’unification des AGN. Mais une grande partie aussi n’est pas due à un tore de poussière, comme imaginé précédemment, mais à un cône creux de grande étendue, puisque dans une direction polaire, perpendiculaire au disque d’accrétion et au tore moléculaire. Le besoin d’obscuration pour une grande fraction des lignes de visée est ainsi satisfait. La figure 5 donne schématiquement les grandes lignes de la nouvelle vision que nous avons aujourd’hui de l’environnement des trous noirs. Même si les AGN de type 1 et 2 ne sont pas tout à fait identiques, le paradigme d’unification basé sur les effets de projection et d’obscuration rencontre des succès.

Fig. 5 : Vue schématique des régions circum-nucléaires autour d’un trou noir super massif. Au centre en bleu, est représenté le disque d’accrétion, en rotation autour du trou noir. Sa taille est inférieure typiquement à une année-lumière. En rose est représenté le rayon de sublimation de la poussière ; c’est là que commence l’écoulement polaire à la fois de la poussière et du gaz, formant un cône creux, autour du vent produit par la pression de radiation de l’AGN. À l’échelle de 30 années-lumière, le tore moléculaire, découplé et non-aligné avec le disque de la galaxie à l’échelle de plusieurs milliers d’al. On y trouve parfois des masers de la molécule d’eau. D’après Hönig (2019).

La grande majorité des galaxies de Seyfert observée par ALMA possède un tore moléculaire découplé du disque hôte, avec une orientation aléatoire. Le tore est en rotation dans une structure en disque très mince. Il est naturel de trouver ces orientations aléatoires, pour du gaz qui provient de régions où le disque galactique est bien plus épais, et où la formation d’étoiles et les épisodes de supernovae peuvent éjecter du gaz au-dessus du plan. Les durées de vie des tores sont de l’ordre de la dizaine ou centaine de milliers d’années, leur gaz alimentant le trou noir de manière intermittente. L’orientation du moment cinétique du gaz, étant aléatoire, l’accrétion de gaz ne pourra faire croître le spin du trou noir que d’une manière lente. Il a été possible dans certaines conditions de mesurer le spin du trou noir ; certaines valeurs sont assez élevées et pourraient provenir de la fusion de galaxies, conduisant à la fusion de leurs trous noirs centraux

Françoise Combes, Collège de France, Observatoire de Paris

Références :

Audibert, A., Combes, F., Garcia-Burillo, S. et al. : 2020, A&A sub

Combes, F., García-Burillo, S., Casasola, V. et al. : 2013, A&A 558, A124

Combes, F., García-Burillo, S., Casasola, V. et al. : 2014, A&A 565, A97

Combes, F., García-Burillo, S., Audibert, A. et al. : 2019, A&A 623, A79

Hönig, S. : 2019, ApJ 884, 171

Ces trous noirs géants qui se cachent au cœur des galaxies

par Sylvain Bouley | Avr 10, 2021 | Zoom Sur

Nous allons voir ici comment un trou noir supermassif se dévoile aux observateurs, et quelles sont ses répercussions sur la galaxie qui l’abrite, pourtant mille fois plus massive et un milliard de fois plus grande. Par ailleurs, ayant participé moi-même pendant cinquante ans à l’étude de ces trous noirs, je me suis permis à plusieurs reprises de prendre un ton personnel pour raconter cette histoire.

Introduction

L’annonce le 11 avril 2019 de l’observation d’un trou noir (« la photo » comme on l’a dit souvent) a déclenché une vague de commentaires superlatifs des médias. Il faut dire qu’il s’agissait effectivement à la fois d’une prouesse technologique et d’une victoire de la science (l’Astronomie, numéro 128, Juin 2019).

Figure 1 – L’image du trou noir au centre de la galaxie m87, dévoilé le 11 février 2019 par l’observation en interférométrie dans le domaine radio. Le cercle en bas à droite représente la taille du lobe. on distingue le « disque d’accrétion », plus intense dans la direction du mouvement. (Collaboration EHT)

En effet, lorsque le physicien allemand Karl Schwarzshild propose en 1916, quelques semaines avant de mourir d’une pneumonie sur le front russe, une solution des équations de la relativité générale qu’Einstein avait publiées l’année précédente, pour une masse sphérique sans rotation, peu de gens y prêtent attention, et Einstein moins que quiconque ; car il ne croira jamais à cette solution, qui prendra en 1967 le nom de « trou noir ».

Nul n’ignore maintenant ce que sont les « trous noirs », ces astres dont rien ne peut s’échapper, ni la lumière, ni la matière, dès qu’elles se trouvent à l’intérieur d’une région de l’espace-temps limitée par une frontière immatérielle nommée : « Event Horizon » (horizon des évènements). Il en est d’ailleurs question presque chaque mois dans les actualités. On connaît actuellement des trous noirs de masses très différentes, depuis quelques masses solaires jusqu’aux trous noirs « supermassifs » de cent mille à des milliards de masses solaires. C’est de ceux-ci que nous allons parler dans cet article. Celui dont on vient de découvrir l’image au centre de la galaxie M87 (Virgo A, Fig. 1) en fait partie : sa masse est égale à 6 milliards de fois celle du Soleil.

Petit historique, des quasars aux trous noirs : 1943, 1952, 1963, trois dates fondatrices dans l’observation et l’identification des trous noirs.

En 1943, un jeune chercheur américain travaillant à l’observatoire McDonald au Texas, Carl Seyfert, publie un article dans lequel il étudie six galaxies possédant un noyau ponctuel brillant dont le spectre présente des raies en émission intenses superposées à un continu bleu. Ce sont les mêmes raies que celles des nébuleuses planétaires, mais beaucoup plus « larges ». Seyfert attribue cette largeur à des vitesses de plusieurs centaines à plusieurs milliers de km/s (c’est une conséquence de l’effet Doppler). La figure 2 montre l’image de l’une de ces galaxies (qu’on appelle simplement « Seyfert »).

Figure 2 – La galaxie de seyfert NGC 5548 obtenue avec le télescope spatial Hubble. on distingue la croix de diffraction prouvant que le noyau n’est pas résolu. La galaxie est vue presque de face. (Nasa)

La deuxième date importante est 1952. À la fin des années quarante, on avait commencé à observer le ciel dans le domaine des ondes radio, entre autre en France avec des radars abandonnés par les allemands après la seconde guerre mondiale. Les américains Baade et Minkowski découvrent alors que deux sources émettant un rayonnement radio intense sont des galaxies : M87 (celle de l’image du trou noir !) et Cygnus A (Figs. 3 et 4). M 87 possède un jet sortant du cœur de la galaxie (on comprendra plus tard son importance). Cygnus A est une galaxie lointaine qui semble constituée de deux galaxies en collision (là aussi on verra plus loin l’importance de cette observation). Ces « radiogalaxies », ainsi que celles qui sont découvertes par la suite, sont beaucoup plus puissantes dans le domaine radio que les autres galaxies, typiquement par un facteur 10000.

Figure 3 – À gauCHE, la galaxie Cygnus A en lumière visible. À drOiTE, image radio en fausses couleurs de la galaxie (petit point au centre) obtenue dans les années 1980, montrant de grands lobes radio très brillants à leurs extrémités, et un filament joignant la galaxie au lobe de droite. La distance projetée sur le ciel entre les extrémités des deux lobes est de 300 000 années-lumière. (Nra0 pour l’image radio)

Quelle est l’explication de ce rayonnement ? Elle ne se fait pas attendre car, par un concours de circonstances dont la science est coutumière – observation et théorie s’épaulant mutuellement – on découvre qu’il correspond à un processus qui se produit dans les nouveaux accélérateurs nommés « synchrotrons ». Il s’agit du rayonnement de particules chargées plongées dans un champ magnétique, se déplaçant à une vitesse très proche de celle de la lumière (on dit qu’elles sont « relativistes »). On l’appelle naturellement « rayonnement synchrotron ». Le britannique Goeffrey Burbidge – il faut préciser son prénom car son épouse, Margaret, joua un rôle considérable dans l’étude des quasars et des galaxies actives – montre immédiatement que l’énergie totale stockée dans un tel système correspond à la transformation en énergie de 100 millions de masses solaires !

Figure 4 – La galaxie m87 prise au télescope Hubble. on distingue le jet provenant du noyau. (Nasa)

Le troisième événement fondateur se produit en 1963. Le 3^ème catalogue de radio-sources de l’observatoire de Cambridge (en Angleterre) vient d’être publié, et la source numéro 273 (appelée 3C 273 donc) a la bonne idée de passer deux fois dernière la Lune en 1962 ; ce qui permet à un radioastronome australien nommé Hazard (ça ne s’invente pas !) de déterminer sa position avec exactitude. Pile à cette position se trouve une étoile bleue de 13^ème magnitude. C’est faible, mais ce n’est pas un problème pour un jeune astronome néerlandais, Marteen Schmidt, qui travaille au Caltech (Pasadena, Californie) et peut utiliser le télescope Hale de 5 mètres du Mont Palomar. Il en prend le spectre et découvre un continu bleu sur lequel se superposent des raies inconnues brillantes et larges. Il comprend qu’il s’agit des raies de la série de Balmer de l’hydrogène, mais toutes décalées de 16% vers le rouge par rapport à leurs longueurs d’onde habituelles. D’autres radiosources sont rapidement identifiées, présentant également un décalage spectral vers le rouge (on utilise le terme anglais plus court de « redshift », ou la lettre z = (l_obsl_émis)/ l_émis, où l_obset l_émissont les longueurs d’onde observée et émise). On les appelle bientôt « quasars », terme contracté de « quasi stellar objects », indiquant qu’ils ressemblent à de simples étoiles sur les photographies [1] (voir sur la figure 5 la page de garde du Time consacré à M. Schmidt). Presque immédiatement, en 1965, l’américain Allan Sandage découvre une population bien plus importante de quasars ne rayonnant pas dans le domaine radio.

Figure 5 – L’annonce de la découverte des quasars par marteen schmidt fait la une du Time Magazine, vol. 87, no 10, 11 mars 1966.

Il est rapidement admis que les redshifts sont dus à l’expansion de l’Univers, et que ces objets se trouvent par conséquent à des distances de plusieurs milliards d’années-lumière. Certains sont également variables en quelques jours (c’est le cas de 3C 273 qui figure depuis cent ans dans le catalogue d’étoiles variables de Harvard), ce qui signifie qu’ils sont petits, puisqu’on les confond avec des étoiles. Et on en arrive à la conclusion inévitable : les quasars ont une puissance de 100 à 1000 galaxies dans un rayon de l’ordre du Système solaire ! [2]

Dès 1964, deux astrophysiciens, le Russe Zeldovich et l’Américain Salpeter, émettent l’hypothèse qu’il s’agit de trous noirs. À l’époque, ceux-ci ont la cote chez les physiciens. J’ai moi-même assisté en 1966 à des cours de relativité générale donnée par le jeune Kip Thorne (qui a reçu en 2019 le prix Nobel pour les ondes gravitationnelles), et ceux qui y étaient avec moi avaient du mal à retenir leur rire lorsque Thorne nous expliquait qu’un homme franchissant l’horizon d’un trou noir pouvait devenir infiniment long ou infiniment plat, et que le temps s’arrêtait pour un observateur extérieur (Fig. 6). Nous avions du mal admettre que ces choses pouvaient avoir le moindre rapport avec les quasars ! Les astronomes et les physiciens n’étaient pas encore prêts à se parler comme ils le feront vingt ans plus tard…

Figure 6. Dessin de PEZ.

Par analogie avec les radiogalaxies qui contiennent également une énorme quantité d’énergie, on attribue à cette époque tout le rayonnement des quasars à du synchrotron, depuis le domaine radio jusqu’au domaine X – car on a commencé à observer dans ces bandes dès 1960 à l’aide de satellites artificiels, et on a découvert qu’ils sont de puissants émetteurs infrarouges, ultraviolets et même X. Et pendant quelque temps, on pense que les quasars sont le lieu d’énormes explosions générant des particules relativistes. Puisque les étoiles à neutrons, très compactes, existent, alors les trous noirs, qui correspondent à un état à peine plus petit et massif, pourraient exister aussi. D’autant que l’on découvre dans un couple stellaire une étoile compacte qui semble bien être un trou noir, Cygnus X1. Et du coup, puisqu’on se convainc que des trous noirs de la masse d’une étoile existent, et puisque leur masse n’a pas grande importance dans la controverse, on admet la possibilité de trous noirs bien plus massifs.

En 1973, deux astronomes soviétiques proposent dans un article devenu « viral » que les trous noirs stellaires sont alimentés par un « disque d’accrétion » (Fig. 7). Pourquoi un disque ? Parce que la matière qui s’approche d’un trou noir a une probabilité très faible d’y tomber directement, mais va tourner autour comme un satellite artificiel autour de la Terre. Grâce à une viscosité provoquée par la turbulence, elle spirale en perdant une grande partie de son énergie de mouvement sous forme de lumière et en se rapprochant lentement du trou noir. Lorsqu’elle atteint enfin son horizon, sa vitesse de rotation est pratiquement égale à celle de la lumière, et elle a perdu jusqu’à la moitié de son énergie de masse (E=Mc²).

Figure 7 – Vue d’artiste d’un disque d’accrétion, avec un jet au centre. Wikipedia

On avait d’autre part dès 1964 fait le parallèle entre les galaxies de Seyfert et les quasars : petite taille, couleur bleue, mêmes raies spectrales (une fois pris en compte le redshift des quasars). On avait réalisé dès lors que les quasars sont simplement des noyaux de galaxies ayant subi dans le passé une phase très « active » ; et c’est à ce moment qu’on avait créé le terme « Noyaux Actifs de Galaxies », AGN en anglais, qui désigne à la fois les quasars et les noyaux des galaxies de Seyfert, puis plus tard également les radiogalaxies comme M 87. Les galaxies de Seyfert sont moins lumineuses que les quasars, mais comme elles sont plus proches, elles sont plus brillantes et accessibles à de plus petits télescopes. C’est à cette époque que j’ai décidé de travailler sur ce sujet et de les observer.

Et finalement en 1977, le britannique Martin Rees montre qu’inévitablement un noyau de galaxie qui contient un amas dense d’étoiles doit évoluer vers la formation d’un trou noir supermassif. En 1978, un jeune chercheur américain, Greg Schields, remarque que le rayonnement de 3C273 n’est pas synchrotron, mais bel et bien dû à ce disque d’accrétion qui va devenir désormais une composante fondamentale des AGN (Fig. 8). Et c’est à partir de ce moment seulement que le paradigme de l’accrétion sur un trou noir supermassif est accepté pour les AGN. Il n’a jamais été remis en cause depuis.

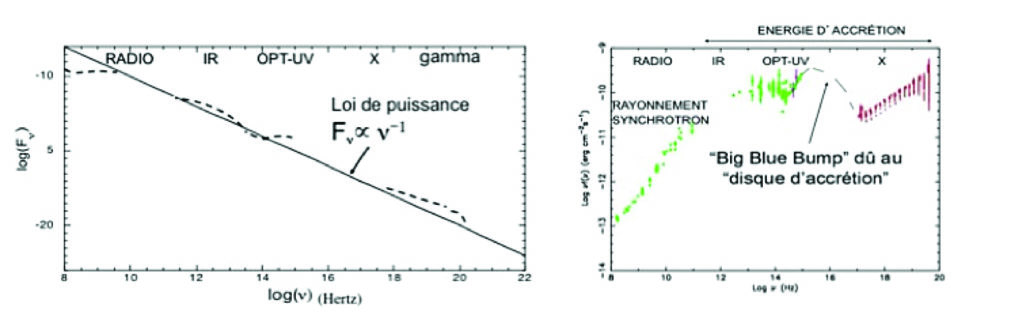
Figure 8 – Distribution de l’énergie du quasar 3C 273, avec deux représentations. Celle de gauche montre pourquoi on a pu confondre ce spectre avec du synchrotron en ν–1 (lire l’actualité p. 8, l’Astronomie n° 124). Crédit S. Collin-Zahn

Les trous noirs « dormants »

Comme le montrent leurs grands redshifts, les quasars sont des objets lointains, situés à des milliards d’années-lumière. Nous les voyons donc tels qu’ils étaient il y des milliards d’années. Que sont-ils devenus maintenant ? Le Britannique Lynden-Bell avait dès 1969 émis l’idée qu’ils se retrouvaient sous forme de quasars « morts » dans les noyaux des galaxies proches de nous, et même dans la nôtre, mais son idée avait fait long feu. Treize ans plus tard, le Polonais Soltan eut l’idée de déterminer la luminosité totale de tous les quasars observés, et il en déduisit, en supposant que l’efficacité de transformation de la masse en énergie était en moyenne de 10% – ce qui est le cas pour les quasars – la masse totale accumulée sous forme de trous noirs. Cette masse étant très supérieure à celle des AGN proches, la conclusion inévitable était qu’elle devait se trouver dans les noyaux des galaxies ordinaires. Curieusement, les calculs qu’il avait effectués avec des hypothèses simplistes se sont avérés justes lorsque l’on a pu déterminer les masses des trous noirs supermassifs situés dans les noyaux des galaxies proches de nous ! On sait donc maintenant que les galaxies ordinaires contiennent un trou noir supermassif éteint, triste résidu d’un quasar qui brilla intensément pendant des dizaines de millions d’années.

Ne croyons cependant pas ce trou noir complètement mort. Quand les quasars s’éteignent, leurs trous noirs deviennent « dormants », mais ils sont susceptibles de se réactiver dès que de la matière s’en approche un peu trop près. Et c’est bien ce qui s’est produit pour le trou noir de notre Galaxie dont nous reparlerons plus loin : bien qu’extrêmement faible en ce moment, il a subi il y a quelques centaines d’années une augmentation de son rayonnement dans le domaine gamma, dont les nuages moléculaires environnants ont gardé la preuve. Il est probable que ce phénomène s’est produit et se reproduira à de nombreuses reprises. L’ogre est toujours là, tapi au centre de la galaxie, et il attend son heure…

Pourquoi les AGN différent-ils tant les uns des autres ?

Avant d’aborder ce problème, il faut préciser qu’un trou noir est un objet extrêmement simple, en fait le plus simple qui existe dans l’Univers : il ne dépend que de deux paramètres, sa masse et sa rotation [3]. Or ce qui avait frappé les découvreurs des quasars et des radiogalaxies, c’est que des objets très différents (on pourrait mentionner les Blac ou lacertides, les blazars, les radiogalaxies, les objets violemment variables ou OVV…) présentent tous la propriété d’émettre une quantité de rayonnement non stellaire très supérieure à celle d’une galaxie « ordinaire ». Il est clair qu’ils tirent tous leur énergie d’un trou noir central. Donc, outre la masse et la rotation du trou noir, il existe des causes extérieures de différentiation.

Influence de l’inclinaison.

Le plus évident, et c’est bien ce qui a été découvert d’abord, c’est que, puisque que le trou noir est nourri par l’intermédiaire d’un disque, l’inclinaison du disque sur la ligne de visée doit jouer un rôle majeur dans l’apparence des objets.

Prenons les noyaux des galaxies de Seyfert. Il en existe deux sortes : les Seyfert 2, dont les raies, relativement étroites, correspondent à quelques centaines de km/s de largeur, et les Seyfert 1, dont les raies, larges, correspondent à plusieurs milliers de km/s. Comme il est naturel, les raies larges proviennent d’une région située à quelques années-lumière du trou noir, tandis que les raies étroites proviennent d’une région située plus loin, à quelques centaines d’années-lumière [4]. En 1985, une étude polarimétrique de la Seyfert 2 NGC 1068 montre que c’est en fait une Seyfert 1 vue en quelque sorte « par la tranche », c’est-à-dire dans une direction proche du plan du disque d’accrétion qui cache la région des raies larges. On en déduit que au moins certaines Seyfert 2 sont des Seyfert 1.

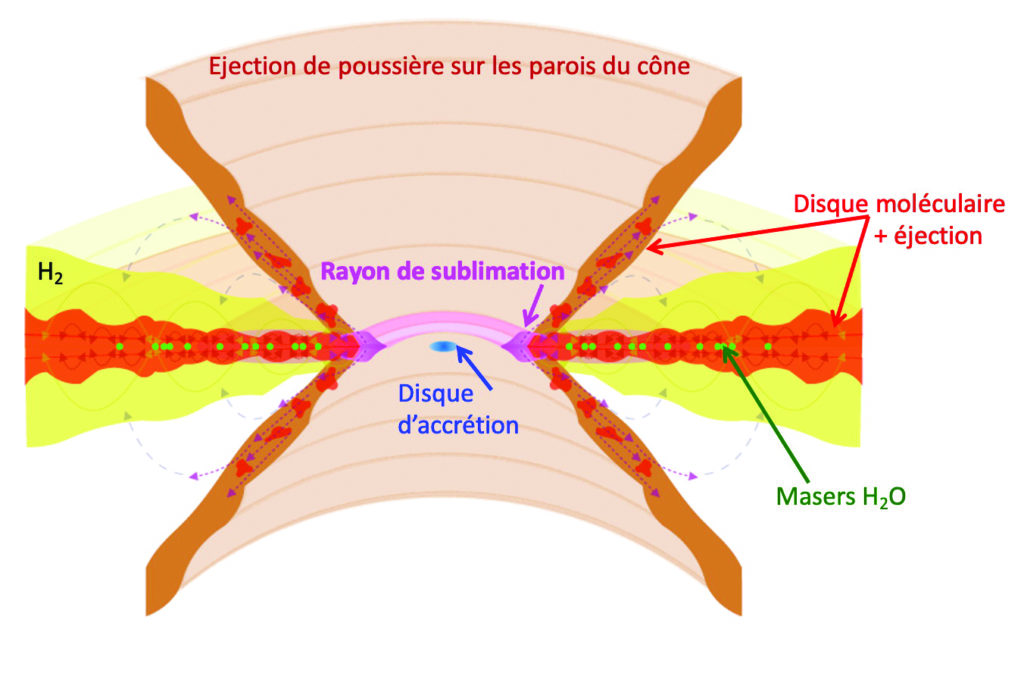
Cette découverte a été la première dans la direction d’une unification des AGN. Elle a abouti quelques années plus tard au schéma suivant, toujours d’actualité (Fig. 9). On reconnait les régions de production des raies larges des Sefert 1, et des raies étroites des Seyfert 2, plus distantes du noyau. On voit que le disque d’accrétion est prolongé par ce que l’on nomme « le tore moléculaire », ou « tore absorbant » sur la figure 9, sorte de disque épais fait de poussières et de molécules. Il constitue la partie externe du disque d’accrétion et cache la partie centrale de l’objet. On ignore d’ailleurs le mécanisme par lequel la matière transite depuis les régions plus extérieures du tore vers le disque lui-même. Sur ce schéma, nous voyons aussi que des objets comme les BLacs et les Blazars sont vus dans la direction d’un jet. On en comprendra plus tard la raison. On commence alors à représenter systématiquement les AGN avec un disque et un jet.

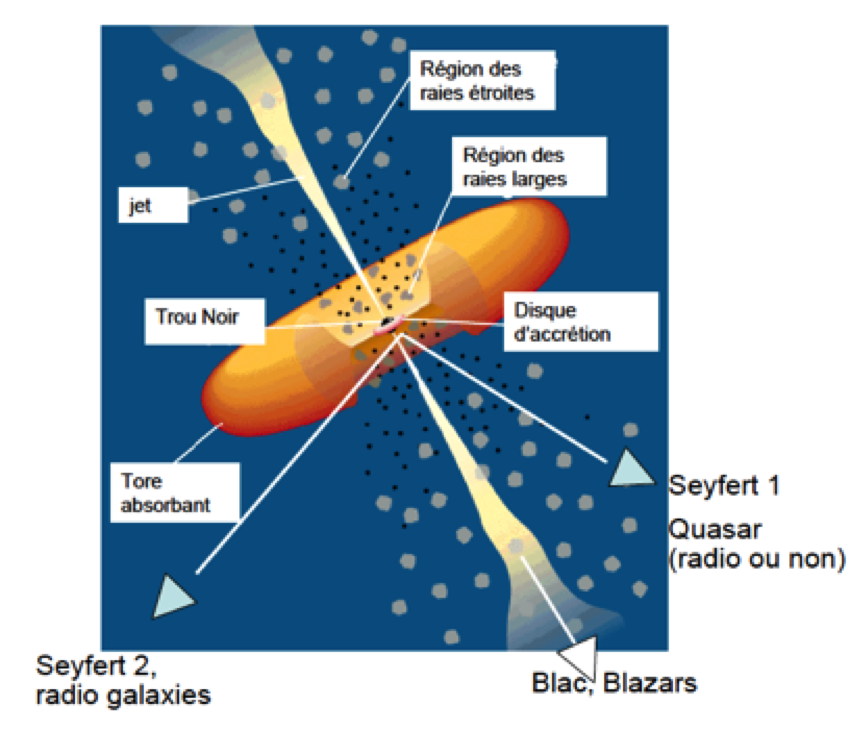
Figure 9 – Schéma unifié des AGN proposé en 1995 par Urry et Padovani

Influence de la masse et du taux d’accrétion

L’une des raisons évidentes de différentiation des trous noirs supermassifs, c’est qu’ils n’ont pas nécessairement la même masse ni la même luminosité. Précisons que désormais je dirai qu’un trou noir « rayonne » une certaine quantité d’énergie, alors qu’il est bien évident que ce n’est pas le trou noir qui rayonne, mais son environnement proche.

Parlons d’abord de la masse. Le principe de la détermination de la masse d’un objet massif quelconque consiste toujours à étudier le mouvement de la matière qui se trouve à proximité, sur laquelle il exerce une influence gravitationnelle dominante. S’il s’agit d’étoiles en orbite, on peut mesurer sa masse en appliquant les lois de Kepler-Newton (c’est ce qui a été fait pour le trou noir central de la Voie lactée). Dans le cas d’un ensemble d’étoiles animées de vitesses aléatoires autour du trou noir, sa masse est à peu près égale à la distance moyenne des étoiles divisée par le carré de la vitesse moyenne [5].

On ne mesure pas la masse d’un trou noir de la même façon s’il est actif ou dormant, ni s’il est proche ou lointain. Ainsi, pour une cinquantaine d’AGN relativement proches, les variations des raies spectrales larges [6] suivies pendant de nombreuses années ont fourni des masses assez précises (disons à un facteur deux près), qui, extrapolées aux autres AGN, ont donné les masses – moins précises – pour des milliers d’autres AGN. Pour les trous noirs dormants, on se sert de la dispersion de vitesse au centre du bulbe [7], là où la masse du trou noir est encore dominante. Naturellement, cette méthode ne peut être utilisée que pour des galaxies assez proches. Enfin, il faut mentionner deux objets exceptionnels où la masse du trou noir est mesurée avec une grande précision. Dans NGC 4258 (M106), on a pu observer les mouvements képlériens de sources à la surface du disque d’accrétion, et on en a déduit la masse du trou noir avec une grande précision (38 millions de masses solaires). Quant au centre de la Voie lactée, une campagne d’observation de vingt ans combinant les mesures de mouvements propres et de vitesses radiales a permis de déterminer la masse d’un objet invisible situé à la position d’une faible radio source, Sagittarius A* (Sgr A*). Il s’agit d’un trou noir de 4,15 millions de masses solaires, une bien petite masse au regard de ceux d’autres galaxies (Fig.10) [8]. Ce trou noir est entouré d’étoiles parcourant des orbites képlériennes. Certaines s’en approchent avec des vitesses de plusieurs milliers de kilomètre par seconde. On a découvert récemment qu’il possède un minuscule disque d’accrétion de moins de 1000 UA de rayon, et qu’il subit de violents sursauts d’activité qui se produisent probablement tout près de son horizon (voir l’Astronomie 130 et / ou, 131, 133, 135).

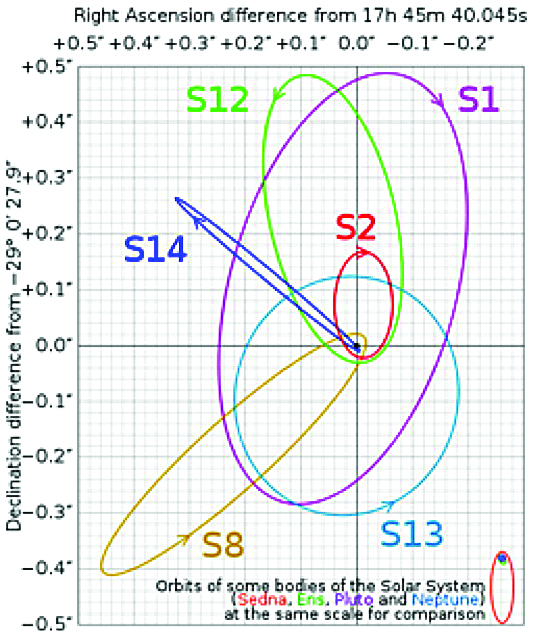
Figure 10 – orbites de quelques étoiles autour de sgr A*. Le trou noir est le point noir. (LESIA – Obs. de Paris)

La découverte la plus inattendue concernant les trous noirs supermassifs, qu’ils soient actifs ou dormants, est la relation qu’ils entretiennent avec le bulbe de la galaxie au centre de laquelle ils se cachent : le trou noir a une masse voisine du millième de celle du bulbe (Fig. 11). Un trou noir, dont le rayon est de l’ordre du millième d’année-lumière, est donc relié fortement au bulbe, dont la dimension est dix à cent millions de fois plus grande ! En fait, aussi étrange que cela paraisse, c’est le trou noir qui a une influence déterminante sur son hôte, par l’intermédiaire des vents et des jets puissants qu’il génère et qui ont pour effet de chauffer et de chasser le gaz, interdisant toute croissance ultérieure de la galaxie. On a l’habitude d’appeler cette rétroaction le « feedback ». Mais il y a une autre cause possible à la relation trou noir/bulbe. En effet, les trous noirs grossissent lors des fusions de galaxies, et les simulations numériques montrent que les fusions ont pour effet de créer des galaxies elliptiques, ou de façon générale des galaxies à gros bulbe. Bref, comme toujours en astrophysique, il est probable que les choses soient complexes et que les deux phénomènes jouent un rôle tour à tour.

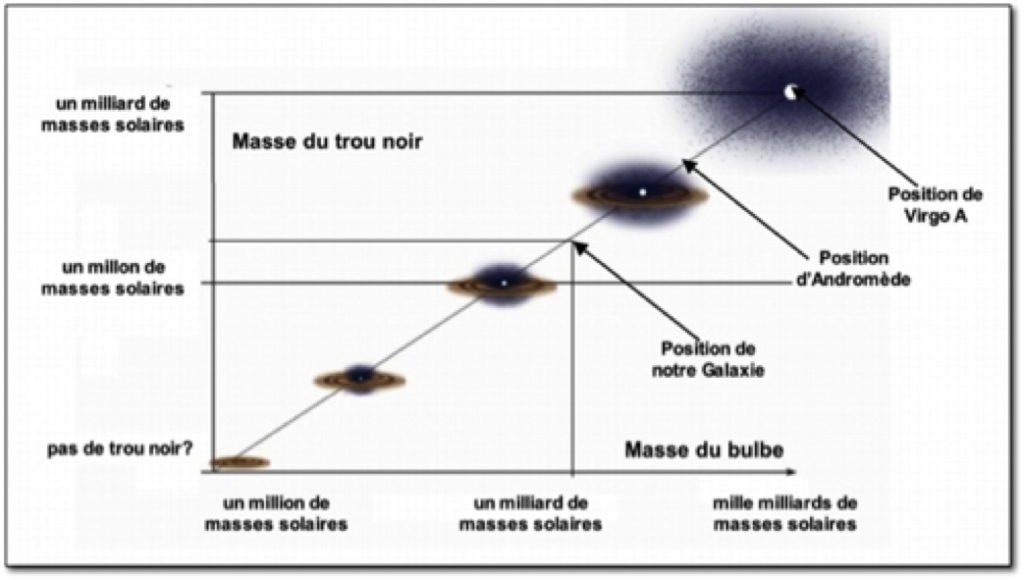
FIgure 11 – La relation entre la masse du trou noir et la masse du bulbe. (S. Collin-Zahn)

Pourtant, ce n’est pas la masse, mais la luminosité du trou noir qui détermine les propriétés des AGN. Intuitivement, on penserait que la luminosité est tout simplement proportionnelle à la quantité de gaz avalée par le trou noir par unité de temps – le taux d’accrétion. Et c’est effectivement ce qui se passe tant que ce taux n’est ni trop grand ni trop petit. La région centrale du disque d’accrétion est alors portée à une température de quelques dizaines de milliers de degrés et il rayonne avec une grande efficacité dans le domaine ultraviolet. C’est le cas des quasars et des galaxies de Seyfert. Mais lorsque le taux d’accrétion est très grand, le disque est si épais que la lumière ne peut pas s’en échapper comme piégée dans cette matière, et qu’elle est engloutie avec elle dans le trou noir. Ces cas sont rares et ne se produisent que lorsque le trou noir est encore peu massif et enrobé d’une épaisse gaine de gaz. À l’inverse, lorsque le taux d’accrétion est trop petit, le disque devient presque transparent, il chauffe et gonfle, les vitesses deviennent aléatoires au point que les particules tombent radialement dans le trou noir sans avoir le temps de rayonner. C’est le cas le plus fréquent des trous noirs dormants, dont fait partie Sagittarius A*.

En fait, ce n’est pas réellement le taux d’accrétion qui est trop grand ou trop petit, mais ce taux ramené à la masse du trou noir. Car pour une masse donnée, un trou noir ne peut rayonner au delà d’une limite appelée « limite d’Eddington [9], qui est proportionnelle à sa masse. Et la quantité qui paraît finalement la plus importante pour façonner les AGN, c’est la luminosité rapportée à la limite d’Eddington.

Les jets

Nous avons mentionné à plusieurs reprises le « jet ». Il est omniprésent dans les radiogalaxies où il domine souvent sur le rayonnement provenant du disque d’accrétion. Par contre, il est quasiment inexistant dans les galaxies de Seyfert et les quasars non radio. Constitué de particules se déplaçant aléatoirement avec des vitesses relativistes, il se déplace également dans son ensemble avec des vitesses proches de celle de la lumière, et il peut se propager très loin du trou noir qui lui a donné naissance.

Or il existe un phénomène que l’on nomme l’aberration relativiste qui se traduit par le fait que la lumière provenant d’une source lumineuse se déplaçant très rapidement est concentrée dans la direction du déplacement. Cet effet est comparable (mais plus accentué) à ce que nous ressentons lorsque nous nous déplaçons en vélo ou en voiture dans une pluie verticale qui nous paraît venir de l’avant. La conséquence est que la lumière est amplifiée pour un observateur regardant la source dans une direction proche du jet (tout comme à vélo sous la pluie, nous sommes plus mouillés devant que dans le dos). C’est ce qui explique que dans certains AGN radio, le rayonnement du jet domine totalement le spectre de l’ensemble de la galaxie. Ce sont les blazars et les Blac, qui sont supposés être vus dans une direction proche du jet (voir le schéma unifié, Fig. 9). L’effet est parfois tellement important qu’on ne voit le jet que dans une seule direction, comme c’est le cas pour M87 et pour Cygnus A montrés sur les figures 3 et 4).

Une conséquence extrême de cet effet est que la lumière produite par le disque d’accrétion est tellement déviée qu’elle finit par parvenir depuis l’arrière du trou noir. Cet effet a été mis en évidence pour la première fois par deux Français travaillant à l’observatoire de Paris-Meudon, Jean-Pierre Luminet en 1983 pour un trou noir sans rotation, et Jean-Alain Marck en 1991 pour un trou noir en rotation (voir Fig. 12). On constate la similitude avec l’image du trou noir de M87 (Fig. 1).

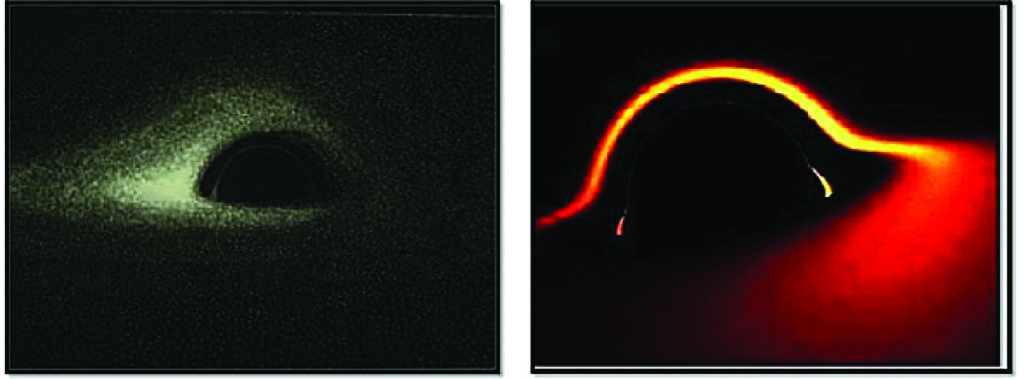
Figure 12 – Simulation de disques d’accrétion : à gauche, pour un trou noir sans rotation, par Jean-Pierre Luminet, en 1983 ; à droite, pour un trou noir en rotation maximum, Jean-Alain Marck, 1991. (Observatoire de Paris-PSL)

Bien qu’ils fascinent depuis qu’on les observe en détail, les jets posent encore aux astrophysiciens bien des questions non résolues : comment expliquer qu’ils restent « collimatés » (c’est à dire très fins) en se propageant jusqu’à des millions d’années-lumière de leur galaxie ? Comment expliquer qu’ils émettent des photons dépassant les mille Giga électrons-volt ? Et surtout, dernière énigme, comment expliquer que les radiogalaxies qui émettent ces jets soient systématiquement des galaxies elliptiques ? La réponse à cette question pourrait bien venir d’un autre paramètre que nous avons négligé, la rotation du trou noir, ou son « spin ».

Le spin

Jusqu’à maintenant, parmi les deux paramètres intrinsèques des trous noirs, nous n’avons mentionné que l’influence de la masse. Nous avons vu qu’elle n’est pas fondamentale : des petits trous noirs (stellaires, même) peuvent avoir presque les mêmes propriétés que les trous noirs les plus massifs. Le deuxième paramètre intrinsèque est la rotation, ou « spin ». Il joue un rôle important à plusieurs titres.

Un trou noir est caractérisé par ce que l’on nomme la dernière orbite circulaire stable, (ISCO en anglais pour « Innermost stable circular orbit ») : c’est l’orbite en deçà de laquelle la matière finit inéluctablement par tomber radialement sur le trou noir sans avoir le temps de perdre de l’énergie. Le rayon de l’ISCO est plus petit pour un trou noir avec rotation (jusqu’à 1,2 rayon gravitationnel [10] pour une rotation maximale) que pour un trou noir sans rotation (6 rayons gravitationnels). Pour en donner une explication simpliste, disons que la matière autour d’un trou noir avec rotation est entrainée dans sa rotation, et peut ainsi se rapprocher du trou noir en continuant à tourner. Ce qui explique que jusqu’à 40% de l’énergie de masse peut être rayonnée pour un trou noir en rotation, contre seulement 6% pour un trou noir sans rotation. C’est une première conséquence du spin.

Par ailleurs, le gaz pouvant se rapprocher au plus près du trou noir s’il est en rotation va émettre des raies spectrales qui subissent le rougissement gravitationnel. Ainsi dans certains AGN, les raies du Fer dans le domaine des rayons X qui sont émises tout près du trou noir sont fortement déformées : elles présentent une aile rouge très étendue (Fig. 13). Cet effet permet d’affirmer que certains trous noirs sont en forte rotation.

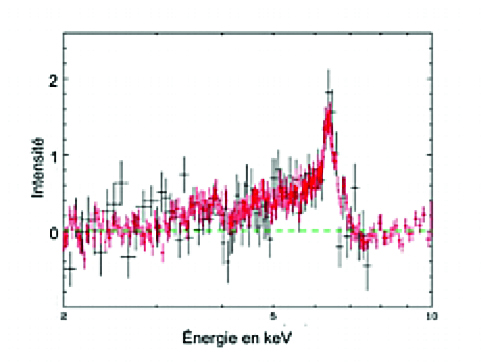
Figure 13 – enregistrement d’une raie du fer dans le domaine X. L’extension de l’aile rouge montre que le gaz émissif est très proche du trou noir et signifie que celui-ci est en rotation rapide. (SMM-Newton, ESA)

La question qu’on se pose alors est : pourquoi certains trous noirs ont-ils un spin, et d’autres n’en ont-ils pas ?

Il existe un processus, appelé Blandford–Znajek du nom de ses deux inventeurs en 1977, disant qu’il est possible d’extraire l’énergie d’un trou noir en rotation par l’intermédiaire du champ magnétique du disque. Des jets puissants pourraient être générés par ce mécanisme près de l’axe du disque d’accrétion. Or cette question rejoint celle de la prédominance de galaxies elliptiques parmi les radiogalaxies. Nous avons mentionné en effet que lorsque deux galaxies spirales se rencontrent et fusionnent, le produit est une galaxie elliptique. Les trous noirs des galaxies se rapprochent alors l’un de l’autre, et forment des trous noirs binaires (Fig. 14). Il est fort probable qu’après avoir tourné pendant quelque temps (disons dix millions d’années) l’un autour de l’autre, ils finissent par fusionner à leur tour, en donnant un trou noir supermassif ayant une forte rotation, comme c’est le cas pour les fusions de trous binaires de masses stellaires observées grâce à leurs ondes gravitationnelles [11]. Au cours du temps, la rotation se ralentira, et le jet disparaitra. Nous retrouvons ici la radiogalaxie Cygnus A mentionnée au début de cet article, dont nous avons vu qu’elle est constituée de deux galaxies en train de fusionner. De même la radiogalaxie M87 au centre de l’amas Virgo, a certainement « cannibalisé » plusieurs autres galaxies de l’amas, devenant elle aussi une galaxie elliptique possédant un jet très énergétique.

FIgure 14 – nGC 6240, deux galaxies en train de fusionner, observées en rayons X par le télescope Chandra. on distingue les deux noyaux actifs, distants de 800 parsecs. (Nasa)

L’environnement

On a vu l’influence de la direction d’observation par rapport à l’axe du disque d’accrétion. Celui-ci peut changer fréquemment de direction en fonction de la matière qui parvient au centre d’une galaxie. C’est donc bien un effet environnemental. Un autre se manifeste dans la forme des sources dans les AGN radio. Elles sont constitués de deux jets symétriques naissant dans le noyau (on ne voit parfois que l’un d’entre eux à cause de l’aberration relativiste), qui s’étendent loin dans l’espace intergalactique. En 1974, Fanaroff et Riley les avaient séparés en deux catégories : les radiogalaxies FRII et les radiogalaxies FRI (voir la figure 3 montrant Cygnus A comme exemple de FRII, et la figure 15 comme exemple de FRI). Les FRII se terminent par des bords brillants – appelés « taches chaudes » ou « hot spots » – tandis que dans les FRI, la luminosité diminue lorsque la distance au centre augmente. La différence entre les deux types est probablement due à la quantité de gaz interstellaire présent dans la galaxie et dans le milieu intergalactique entourant la galaxie.

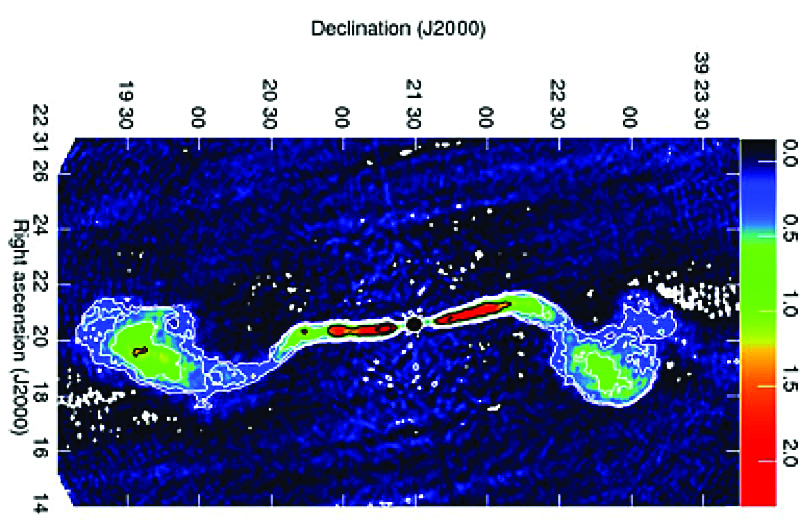
Figure 15 – Carte radio de la radiogalaxie 3C 449 de type Fr i.

Perspective

Il y aurait évidemment encore beaucoup à dire sur les trous noirs supermassifs. Un paradoxe sur lequel il a été peu insisté doit cependant être souligné : les trous noirs jouent le rôle d’absorbeurs de matière autant que d’éjecteurs par leurs jets ou par leurs vents. De ces derniers il a été peu question, car ils se produisent relativement loin du trou noir. Ils ont diverses causes, comme la pression du rayonnement ou l’évaporation due à la température élevée qu’atteint le gaz en se rapprochant du trou noir. Ils empêchent une partie importante de la matière de parvenir jusqu’au trou noir. Ils peuvent être dévastateurs pour l’environnement galactique et jouer un rôle important dans la relation entre les trous noirs et les galaxies. L’avenir nous en dira certainement beaucoup sur ce sujet encore assez nouveau.

Suzy COLLIN-ZAHN | Observatoire de Paris

Notes

[1] Une autre de ces radiosources, 3C48, avait été identifiée dès 1960 à une faible étoile bleue, mais on n’avait pas réussi à interpréter les raies de son spectre, et pour cause : elles étaient décalées de 37% par rapport à leurs longueurs d’onde habituelles.

[2] Je passe sous silence une discussion qu’on a appelée « la controverse du redshift » avec les partisans d’un redshift dû à une loi physique inconnue. Elle a débuté en 1965 et ne s’est apaisée – pas complètement – qu’en 1978 après une confrontation violente dans un congrès – à laquelle j’ai assisté.

[3] En fait , il dépend également d’un troisième paramètre, la charge, mais on il est admis que celle-ci est nulle, car la matière qui pénètre dans un trou noir n’est pas chargée.

[4] J’ai contribué moi-même dans ma thèse en 1968 à établir ce modèle.

[5] Cette relation suppose que l’ensemble des étoiles a atteint un état d’équilibre.

[6] J’ai annoncé la première en 1968 que les raies spectrales larges devaient varier en quelques années. Mais c’est en 1982 seulement que la méthode de détermination des masses a été formalisée et que des observations intensives ont commencé.

[7] Le bulbe est cette région brillante centrale sphéroïdale, importante dans les galaxies spirales des premiers types, et à laquelle se réduisent complètement les galaxies elliptiques

[8] Notons que des chercheurs français ont participé activement à la mise au point de l’optique adaptative nécessaire aux observations.

[9] Cette limite, découverte par le célèbre astronome britannique Arthur Eddington, correspond à l’égalité entre la force du rayonnement qui repousse la matière et la force gravitationnelle du trou noir qui l’attire.

[10] Le rayon gravitationnel est égal à GM/c², où G est la constante de la gravitation et c la vitesse de la lumière. Il est de 1,5 km pour un astre ayant la masse du Soleil. On voit qu’il est proportionnel à la masse, ce qui explique que la densité moyenne des trous noirs supermassifs soit relativement faible, contrairement à ce que l’on pense souvent.

[11] Ces fusions pourront être observées par l’instrument spatial LISA lorsqu’il sera mis en service… dans une vingtaine d’années!

Glossaire

Quasar : galaxie rendue extrêmement lumineuse à cause de la présence en son centre d’un trou noir supermassif très actif, car disposant de beaucoup de gaz à avaler.

Seyfert (galaxies de) : Galaxies découvertes par Carl Seyfert, ayant un noyau bleu très brillant d’aspect stellaire dont le spectre présente des raies en émission intenses et larges.

AGN : « Active Galactic Nuclei » en anglais, expression utilisée pour désigner les galaxies dont le trou noir central est alimenté par de la matière y tombant en quantités importantes. Les quasars, les galaxies de Seyfert et les radio galaxies sont des AGN.

BLac (ou lacertides) : radiogalaxies dont la direction d’observation est proche du jet, ce qui a pour effet d’amplifier le rayonnement qu’il émet.

Blazar : quasars radio (plus lumineux que les radiogalaxies) dont la direction d’observation est proche du jet, ce qui a pour effet d’amplifier le rayonnement qu’il émet.

radiogalaxies : galaxies dont le rayonnement radio est beaucoup plus intense que le rayonnement visible.

OVV : objets présentant des variations optiques violents et rapides.

Trous noirs – Un nouveau test de relativité générale

par Sylvain Bouley | Avr 10, 2021 | Zoom Sur

L’équipe internationale en charge de l’instrument GRAVITY a annoncé récemment la détection de la précession de Schwarzschild sur l’orbite de l’étoile S2, la plus proche du trou noir supermassif au centre de la Voie Lactée.

Pour comprendre ce que cette détection signifie, il est utile de faire un pas en arrière et de considérer l’évolution des idées sur la notion d’orbite des corps célestes, avant de se lancer dans le cœur du sujet des détails de cette détection. Nous allons voir que la mesure de GRAVITY constitue une dernière étape sur une route jalonnée depuis deux millénaires et demi par Eudoxe de Cnide, Kepler et Einstein.

Orbites des corps célestes pour les anciens Grecs : Eudoxe de Cnide

Tout commence par Pythagore (autour de 550 avant notre ère). Son école fort ésotérique apporte deux avancées considérables. Tout d’abord, les Pythagoriciens tiennent pour principe premier des choses le nombre. Ce début de mathématisation du monde est promis à un brillant et long avenir. Ensuite, les Pythagoriciens proposent une vision toute nouvelle sur la géométrie. Le fameux théorème de Pythagore (le carré de l’hypoténuse de tout triangle rectangle …) était déjà connu en pratique des Égyptiens, qui avaient noté cette particularité dans tel ou tel triangle particulier. L’apport crucial de Pythagore, c’est de poser que ceci est valable pour tout triangle rectangle, début de systématisation de la géométrie, début d’une vision scientifique moderne, se dégageant d’un savoir purement pratique (tel que l’était, par exemple, celui des Égyptiens antiques).

Platon (autour de 400 avant notre ère) propose un modèle du cosmos basé sur des sphères imbriquées (on reconnaît là l’influence de la mathématisation du monde proposée par les Pythagoriciens). La Terre est au centre, entourée des sphères de l’eau, de l’air et du feu. Les astres se meuvent au-delà, à des distances croissantes (vient d’abord la Lune, puis les autres planètes connues et le Soleil, et enfin la sphère des étoiles lointaines fixes). Ce modèle est développé par Eudoxe de Cnide (contemporain de Platon) qui postule que les astres se déplacent le long des sphères imbriquées de Platon en suivant des orbites circulaires et uniformes. Nous voici devant le premier modèle explicite d’orbite d’un corps céleste : Eudoxe peut être ainsi considéré comme le premier astronome au sens moderne du terme. Nous allons voir que l’observation récente de GRAVITY est une héritière très lointaine de ce pionnier.

Figure 1 – Les systèmes du monde Copernic (gauche) et d’Eudoxe (à droite) et de. source : Histoire générale des sciences, dir. r. taton, tome ii.

Orbites des corps célestes de la renaissance à l’époque classique : Kepler

Malgré les développements considérables apportés par Ptolémée (au Ier siècle de notre ère) au modèle d’Eudoxe, on peut considérer que les éléments de base de la compréhension du cosmos n’ont pas évolué de façon radicale avant le XVIe siècle. Cette gigantesque plage de temps illustre bien le caractère véritablement stupéfiant des avancées des VIe et Ve siècles de la Grèce antique. Il revient à trois scientifiques des XVIe et XVIIe siècles de proposer le cadre conceptuel suivant : Nicolas Copernic (~1530), Tycho Brahé (~1580) et Johannes Kepler (~1610). La révolution copernicienne consiste à placer non plus la Terre, mais le Soleil au centre du cosmos. Les astres sont toujours considérés en orbite circulaire et uniforme autour du Soleil (voir la Figure 1 qui compare le système du monde hérité d’Eudoxe à celui de Copernic). Tycho Brahé réalise des observations d’une superbe précision, et sur une très grande quantité de sources, qui seront la base de la systématisation suivante, entreprise par Kepler au tournant du XVIIe siècle.

Kepler est le véritable point de référence auquel doit se comparer le résultat de l’équipe GRAVITY. Faisant la synthèse des apports de Copernic et de Tycho, il aboutit aux fameuses lois de Kepler, qui apportent deux éléments nouveaux fondamentaux. Tout d’abord, il a la première intuition du rôle de moteur joué par le Soleil dans le mouvement des astres, alors que les descriptions précédentes se contentaient d’entériner le fait que les astres tournent, soit autour de la Terre, soit autour du Soleil, sans voir de lien de cause à effet entre la présence du corps central et le mouvement des astres autour de celui-ci. Ensuite, Kepler est amené, grâce aux superbes observations de Tycho, à battre en brèche la théorie du mouvement circulaire et uniforme des astres (datant d’Eudoxe, donc de 2000 ans en arrière) et à le remplacer par un mouvement elliptique. Avec Newton (~1680), sa loi du mouvement et sa loi de gravitation universelle, les avancées de Kepler sont confirmées et incluses dans un système d’explication beaucoup plus vaste, qui forme l’une des pierres angulaires de l’astronomie jusqu’à Einstein.

Orbites des corps célestes de la relativité générale : Einstein

Einstein est l’héritier direct de Newton. C’est lui qui reformule les lois de la gravitation en 1915, aboutissant aux lois de la relativité générale, qui englobent et dépassent considérablement la théorie newtonienne. Ce n’est pas le lieu ici d’expliquer son cheminement. Il convient par contre de discuter l’une des conséquences de la relativité générale sur les orbites des corps célestes. Einstein aboutit à la prédiction que les orbites des planètes autour du Soleil ne doivent pas suivre des ellipses kepleriennes. Elles vont peu à peu se décaler pour former une rosace, dans un mouvement de précession du périhélie, le point de l’orbite le plus rapproché du Soleil (Figure 2). Einstein se souvient alors que l’astronome français Le Verrier avait mis en évidence en 1859 à l’Observatoire de Paris le fait que la planète Mercure (la plus proche du Soleil, et donc la plus fortement soumise à sa gravitation) exhibait un mouvement inexpliqué, en désaccord avec les lois de Kepler et de Newton. Einstein se jette sur ce problème et détermine ce que prédit sa propre théorie. Celle-ci explique exactement l’incohérence rapportée par Le Verrier. Einstein, d’après ce qu’il a lui-même rapporté, « est resté sans voix pendant plusieurs jours à cause de [s]on excitation » suite à cette toute première vérification expérimentale de sa nouvelle théorie, qui valide son travail acharné réalisé pendant la décennie qui précède. La mesure récente de l’équipe GRAVITY est la dernière vérification expérimentale de ce même effet, dans un contexte très différent.

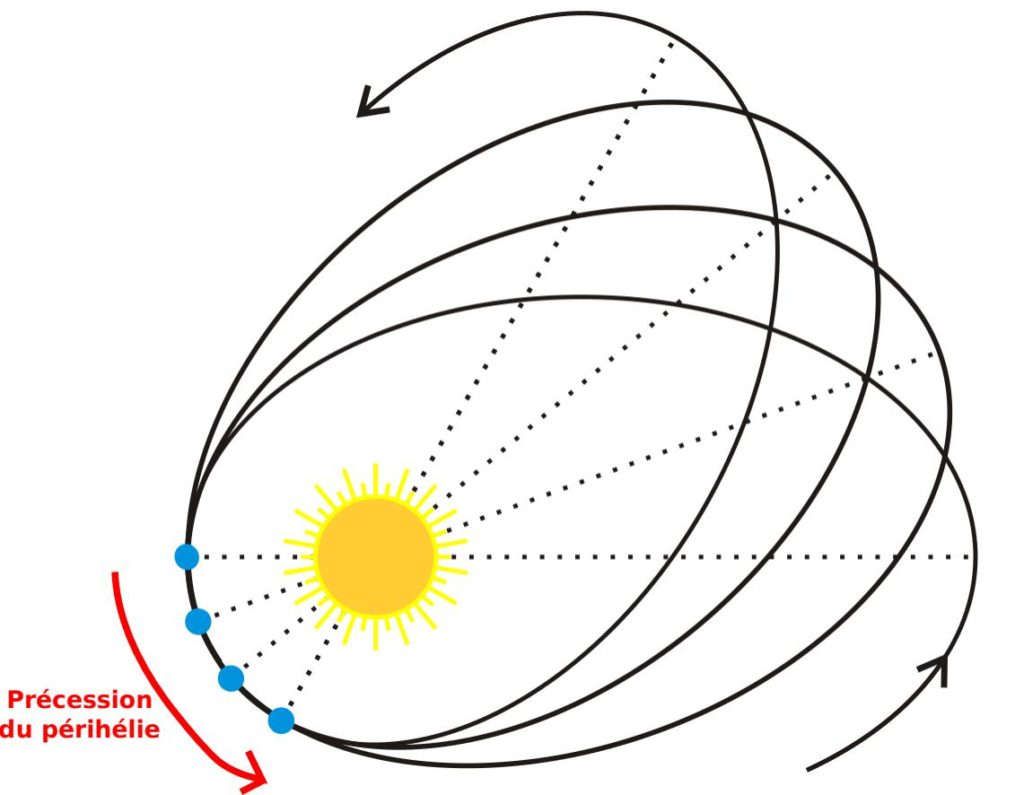
Figure 2 – orbite d’une planète autour du soleil d’après la relativité générale. L’ellipse suivie par la planète se décale peu à peu, entraînant le périhélie dans un lent mouvement de précession indiqué par la succession des cercles bleus (très exagéré bien entendu sur ce schéma). (source : modifié à partir de Wikipedia – article apsidal precession).

Détecter la précession de Schwarzschild sur l’orbite de l’étoile S2 : GRAVITY

L’instrument GRAVITY du Very Large Telescope (VLT) de l’ESO a déjà été présenté dans l’Astronomie Magazine par deux articles de Guy Perrin (avril 2011, octobre 2016). Rappelons seulement ici qu’il s’agit de recombiner la lumière issue des quatre télescopes géants de 8 mètres de diamètre du VLT, afin de réaliser un interféromètre en longueur d’onde infrarouge. Cet instrument, qui a vu sa première lumière en 2016, permet ainsi d’atteindre une précision de 30 microsecondes d’angle dans la mesure du déplacement d’un objet sur le ciel. Il faut s’attarder un instant sur ce chiffre. Il s’agit de la taille angulaire d’un cheveu situé à Barcelone et vu depuis Paris… Cette stupéfiante précision a été cruciale dans la détection dont nous allons parler maintenant.

GRAVITY observe en particulier les abords du trou noir de 4 millions de fois la masse du Soleil qui se trouve au centre de notre Galaxie, Sagittarius A* (Sgr A* dans la suite). Cet objet compact est entouré d’un amas d’étoiles dont la plus proche, appelée S2, parvient à son péricentre à 120 unités astronomiques seulement du trou noir (la taille du système solaire environ, voir la Figure 3). A cette distance, des effets de relativité générale sur l’orbite sont attendus, et en particulier l’effet de précession du péricentre, le même que celui qui affecte Mercure autour du Soleil.

L’objectif de la collaboration GRAVITY était de mettre en évidence la précession du péricentre de l’étoile S2 autour de Sgr A*. On parle de précession de Schwarzschild pour préciser qu’on s’intéresse à l’effet obtenu près d’un trou noir considéré comme sans rotation, appelé trou noir de Schwarzschild. Cette dénomination fait référence au découvreur de cet objet, Karl Schwarzschild, qui publia la première solution de trou noir (sans savoir alors qu’il s’agissait de ce type d’objet exotique) en janvier 1916 (soit 2 mois seulement après qu’Einstein ait publié son propre article sur les équations de la relativité générale en novembre 1915).

Il convient d’insister sur le fait que, si l’effet observé par GRAVITY est le même que celui étudié par Einstein dès 1915, le contexte est entièrement différent. La détection de l’effet de précession du péricentre dans l’environnement proche d’un trou noir supermassif est une validation beaucoup plus puissante de la théorie que cette même validation dans l’environnement solaire.

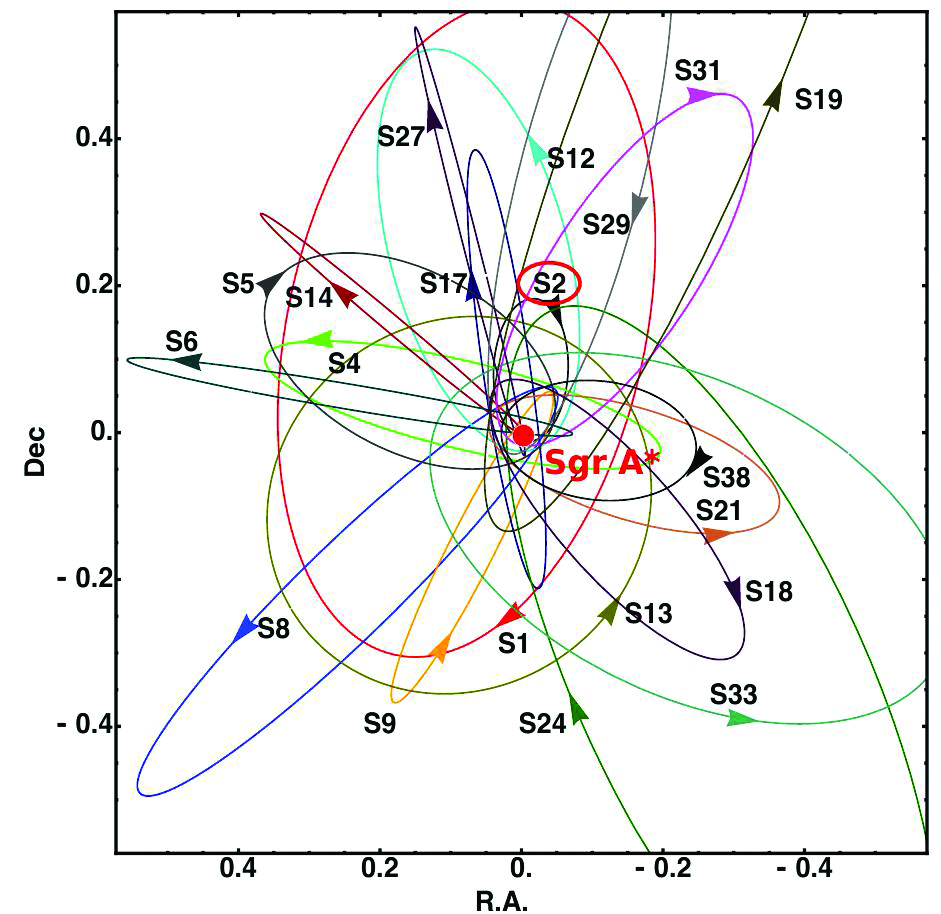
Figure 3 – L’amas d’étoiles situé autour du trou noir supermassif sgr A* au centre de la Galaxie. L’étoile s2 observée par Gravity, la plus proche du trou noir, est entourée en rouge. (Gillessen et al. ,2009)

En quoi consiste la détection par GRAVITY

La détection d’un mouvement de précession du péricentre nécessite à la fois un suivi sur le très long terme de l’étoile S2 (qui a une période orbitale de 15 ans), et une précision de mesure extrême au moment du passage au péricentre. La très longue base temporelle a été rendue possible par les observations continues de S2 effectuées depuis 2002 par la caméra infrarouge NACO du VLT. Les données GRAVITY ont quant à elles permis de suivre avec une précision fantastique le passage de S2 à son péricentre en mai 2018. C’est vraiment la combinaison de ces deux jeux de données (avec l’ajout des données spectroscopiques obtenues par l’instrument SINFONI du VLT) qui a permis une détection claire cette année.

Une fois les données orbitales enregistrées par NACO et GRAVITY, il a fallu ajuster un modèle théorique d’orbite à la trajectoire de S2. L’équipe GRAVITY a utilisé une approximation de la relativité générale, le formalisme post-Newtonien, qui permet de simplifier le problème tout en conservant une précision suffisante pour le cas traité ici. La Figure 4 montre le résultat crucial de l’article récent de la collaboration GRAVITY. Le modèle post-Newtonien ajuste parfaitement les données, alors qu’un modèle n’incluant pas la précession de Schwarzschild est exclu. Une étude statistique précise a permis de démontrer que la détection de la précession de Schwarzschild peut être considérée comme décisive.

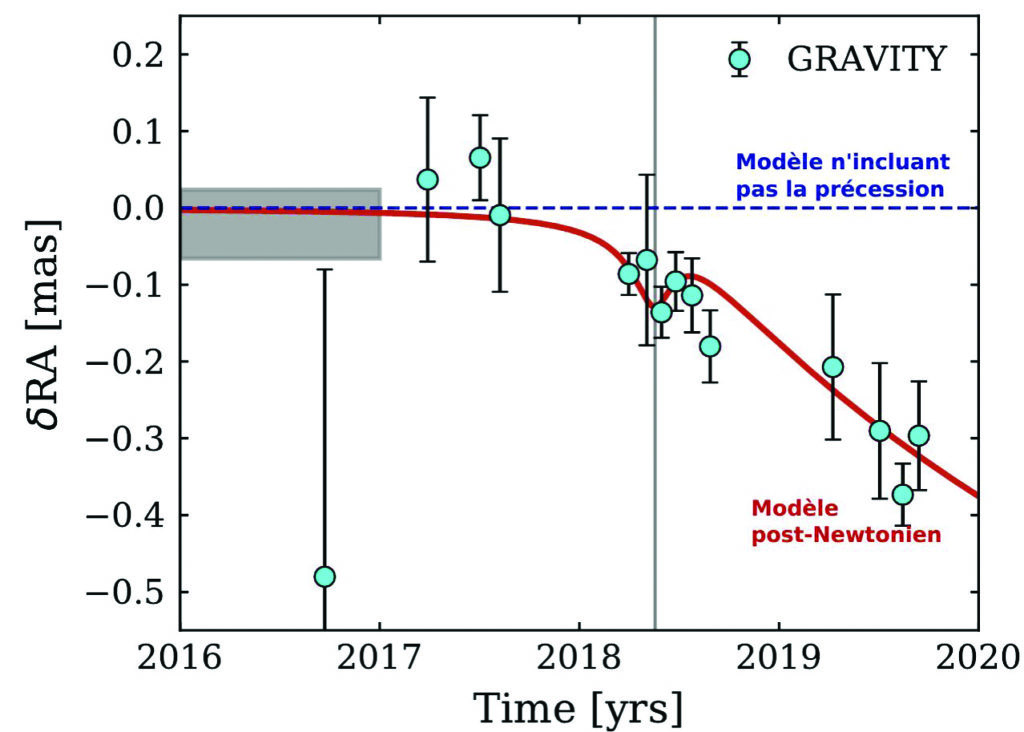
Figure 4 – Détection par Gravity de la précession de schwarzschild sur l’orbite de l’étoile s2. Les points de données en couleur cyan sont parfaitement ajustés par le modèle post- newtonien (approximation de la relativité générale complète, en rouge), alors qu’un modèle n’incluant pas la précession de schwarzschild (en bleu) est exclu. (Gravity collaboration, 2020)

De 1915 à 2020

Comme l’avait fait Einstein en 1915 pour Mercure, l’équipe GRAVITY a pu monter le parfait accord entre la prédiction de la relativité générale et la mesure de la précession de Schwarzschild de l’orbite de l’étoile S2. La Figure 5 compare une lettre d’Einstein portant sur son test de 1915 sur Mercure avec la formule de la précession de Schwarzschild utilisée dans l’article récent de la collaboration GRAVITY. C’est bien le même phénomène qui est étudié !

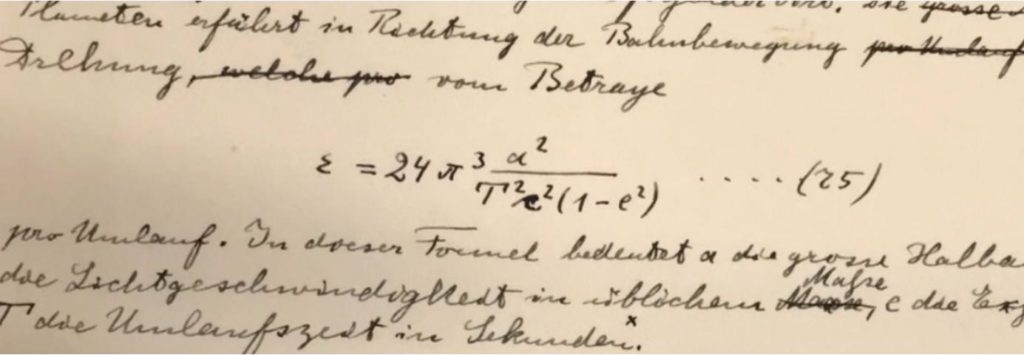
FIgure 5 – Texte d’einstein de 1915 relatif à la détection du mouvement de précession relativiste de mercure autour du soleil validant sa théorie. (en Médaillon) extrait de l’article de la collaboration Gravity mettant en évidence le même effet sur l’étoile s2 autour du trou noir supermassif au centre de notre Galaxie. Nous laissons à nos lecteurs les plus assidus le soin de montrer l’équivalence des deux formules.

Frédéric VINCENT | CNRS – Observatoire de Paris

« Entrées précédentes

Entrées suivantes »