L’équipe internationale en charge de l’instrument GRAVITY a annoncé récemment la détection de la précession de Schwarzschild sur l’orbite de l’étoile S2, la plus proche du trou noir supermassif au centre de la Voie Lactée.

Pour comprendre ce que cette détection signifie, il est utile de faire un pas en arrière et de considérer l’évolution des idées sur la notion d’orbite des corps célestes, avant de se lancer dans le cœur du sujet des détails de cette détection. Nous allons voir que la mesure de GRAVITY constitue une dernière étape sur une route jalonnée depuis deux millénaires et demi par Eudoxe de Cnide, Kepler et Einstein.
Orbites des corps célestes pour les anciens Grecs : Eudoxe de Cnide
Tout commence par Pythagore (autour de 550 avant notre ère). Son école fort ésotérique apporte deux avancées considérables. Tout d’abord, les Pythagoriciens tiennent pour principe premier des choses le nombre. Ce début de mathématisation du monde est promis à un brillant et long avenir. Ensuite, les Pythagoriciens proposent une vision toute nouvelle sur la géométrie. Le fameux théorème de Pythagore (le carré de l’hypoténuse de tout triangle rectangle …) était déjà connu en pratique des Égyptiens, qui avaient noté cette particularité dans tel ou tel triangle particulier. L’apport crucial de Pythagore, c’est de poser que ceci est valable pour tout triangle rectangle, début de systématisation de la géométrie, début d’une vision scientifique moderne, se dégageant d’un savoir purement pratique (tel que l’était, par exemple, celui des Égyptiens antiques).
Platon (autour de 400 avant notre ère) propose un modèle du cosmos basé sur des sphères imbriquées (on reconnaît là l’influence de la mathématisation du monde proposée par les Pythagoriciens). La Terre est au centre, entourée des sphères de l’eau, de l’air et du feu. Les astres se meuvent au-delà, à des distances croissantes (vient d’abord la Lune, puis les autres planètes connues et le Soleil, et enfin la sphère des étoiles lointaines fixes). Ce modèle est développé par Eudoxe de Cnide (contemporain de Platon) qui postule que les astres se déplacent le long des sphères imbriquées de Platon en suivant des orbites circulaires et uniformes. Nous voici devant le premier modèle explicite d’orbite d’un corps céleste : Eudoxe peut être ainsi considéré comme le premier astronome au sens moderne du terme. Nous allons voir que l’observation récente de GRAVITY est une héritière très lointaine de ce pionnier.

Figure 1 – Les systèmes du monde Copernic (gauche) et d’Eudoxe (à droite) et de. source : Histoire générale des sciences, dir. r. taton, tome ii.
Orbites des corps célestes de la renaissance à l’époque classique : Kepler
Malgré les développements considérables apportés par Ptolémée (au Ier siècle de notre ère) au modèle d’Eudoxe, on peut considérer que les éléments de base de la compréhension du cosmos n’ont pas évolué de façon radicale avant le XVIe siècle. Cette gigantesque plage de temps illustre bien le caractère véritablement stupéfiant des avancées des VIe et Ve siècles de la Grèce antique. Il revient à trois scientifiques des XVIe et XVIIe siècles de proposer le cadre conceptuel suivant : Nicolas Copernic (~1530), Tycho Brahé (~1580) et Johannes Kepler (~1610). La révolution copernicienne consiste à placer non plus la Terre, mais le Soleil au centre du cosmos. Les astres sont toujours considérés en orbite circulaire et uniforme autour du Soleil (voir la Figure 1 qui compare le système du monde hérité d’Eudoxe à celui de Copernic). Tycho Brahé réalise des observations d’une superbe précision, et sur une très grande quantité de sources, qui seront la base de la systématisation suivante, entreprise par Kepler au tournant du XVIIe siècle.
Kepler est le véritable point de référence auquel doit se comparer le résultat de l’équipe GRAVITY. Faisant la synthèse des apports de Copernic et de Tycho, il aboutit aux fameuses lois de Kepler, qui apportent deux éléments nouveaux fondamentaux. Tout d’abord, il a la première intuition du rôle de moteur joué par le Soleil dans le mouvement des astres, alors que les descriptions précédentes se contentaient d’entériner le fait que les astres tournent, soit autour de la Terre, soit autour du Soleil, sans voir de lien de cause à effet entre la présence du corps central et le mouvement des astres autour de celui-ci. Ensuite, Kepler est amené, grâce aux superbes observations de Tycho, à battre en brèche la théorie du mouvement circulaire et uniforme des astres (datant d’Eudoxe, donc de 2000 ans en arrière) et à le remplacer par un mouvement elliptique. Avec Newton (~1680), sa loi du mouvement et sa loi de gravitation universelle, les avancées de Kepler sont confirmées et incluses dans un système d’explication beaucoup plus vaste, qui forme l’une des pierres angulaires de l’astronomie jusqu’à Einstein.
Orbites des corps célestes de la relativité générale : Einstein
Einstein est l’héritier direct de Newton. C’est lui qui reformule les lois de la gravitation en 1915, aboutissant aux lois de la relativité générale, qui englobent et dépassent considérablement la théorie newtonienne. Ce n’est pas le lieu ici d’expliquer son cheminement. Il convient par contre de discuter l’une des conséquences de la relativité générale sur les orbites des corps célestes. Einstein aboutit à la prédiction que les orbites des planètes autour du Soleil ne doivent pas suivre des ellipses kepleriennes. Elles vont peu à peu se décaler pour former une rosace, dans un mouvement de précession du périhélie, le point de l’orbite le plus rapproché du Soleil (Figure 2). Einstein se souvient alors que l’astronome français Le Verrier avait mis en évidence en 1859 à l’Observatoire de Paris le fait que la planète Mercure (la plus proche du Soleil, et donc la plus fortement soumise à sa gravitation) exhibait un mouvement inexpliqué, en désaccord avec les lois de Kepler et de Newton. Einstein se jette sur ce problème et détermine ce que prédit sa propre théorie. Celle-ci explique exactement l’incohérence rapportée par Le Verrier. Einstein, d’après ce qu’il a lui-même rapporté, « est resté sans voix pendant plusieurs jours à cause de [s]on excitation » suite à cette toute première vérification expérimentale de sa nouvelle théorie, qui valide son travail acharné réalisé pendant la décennie qui précède. La mesure récente de l’équipe GRAVITY est la dernière vérification expérimentale de ce même effet, dans un contexte très différent.
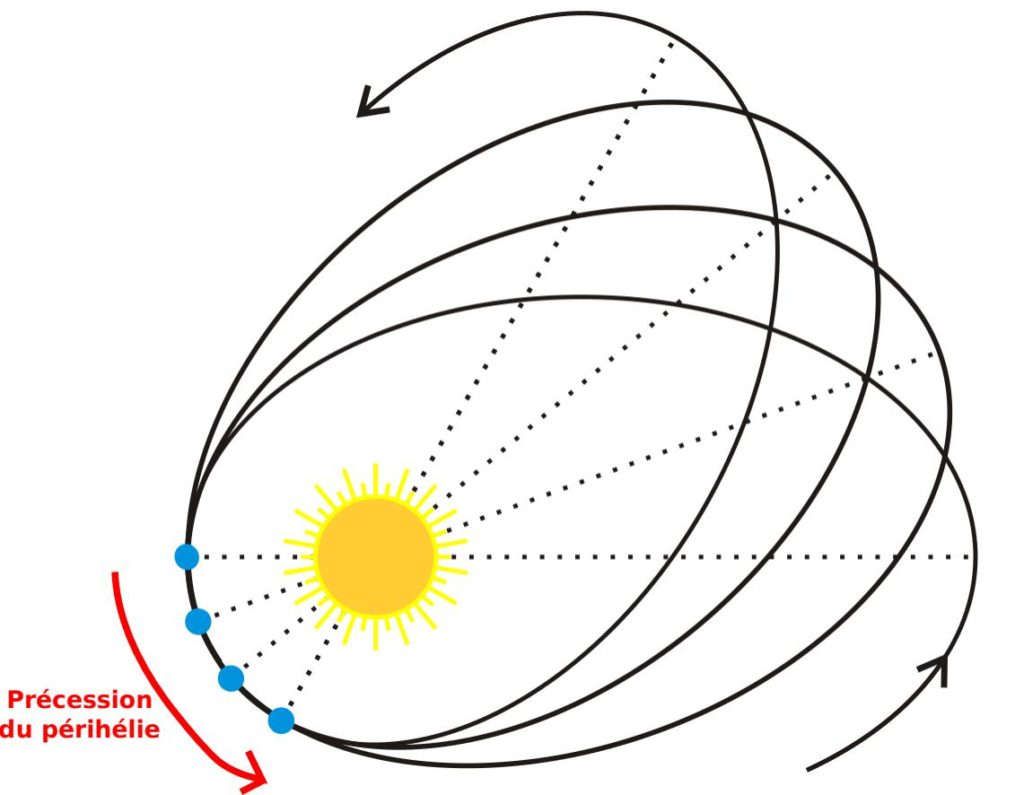
Figure 2 – orbite d’une planète autour du soleil d’après la relativité générale. L’ellipse suivie par la planète se décale peu à peu, entraînant le périhélie dans un lent mouvement de précession indiqué par la succession des cercles bleus (très exagéré bien entendu sur ce schéma). (source : modifié à partir de Wikipedia – article apsidal precession).
Détecter la précession de Schwarzschild sur l’orbite de l’étoile S2 : GRAVITY
L’instrument GRAVITY du Very Large Telescope (VLT) de l’ESO a déjà été présenté dans l’Astronomie Magazine par deux articles de Guy Perrin (avril 2011, octobre 2016). Rappelons seulement ici qu’il s’agit de recombiner la lumière issue des quatre télescopes géants de 8 mètres de diamètre du VLT, afin de réaliser un interféromètre en longueur d’onde infrarouge. Cet instrument, qui a vu sa première lumière en 2016, permet ainsi d’atteindre une précision de 30 microsecondes d’angle dans la mesure du déplacement d’un objet sur le ciel. Il faut s’attarder un instant sur ce chiffre. Il s’agit de la taille angulaire d’un cheveu situé à Barcelone et vu depuis Paris… Cette stupéfiante précision a été cruciale dans la détection dont nous allons parler maintenant.
GRAVITY observe en particulier les abords du trou noir de 4 millions de fois la masse du Soleil qui se trouve au centre de notre Galaxie, Sagittarius A* (Sgr A* dans la suite). Cet objet compact est entouré d’un amas d’étoiles dont la plus proche, appelée S2, parvient à son péricentre à 120 unités astronomiques seulement du trou noir (la taille du système solaire environ, voir la Figure 3). A cette distance, des effets de relativité générale sur l’orbite sont attendus, et en particulier l’effet de précession du péricentre, le même que celui qui affecte Mercure autour du Soleil.
L’objectif de la collaboration GRAVITY était de mettre en évidence la précession du péricentre de l’étoile S2 autour de Sgr A*. On parle de précession de Schwarzschild pour préciser qu’on s’intéresse à l’effet obtenu près d’un trou noir considéré comme sans rotation, appelé trou noir de Schwarzschild. Cette dénomination fait référence au découvreur de cet objet, Karl Schwarzschild, qui publia la première solution de trou noir (sans savoir alors qu’il s’agissait de ce type d’objet exotique) en janvier 1916 (soit 2 mois seulement après qu’Einstein ait publié son propre article sur les équations de la relativité générale en novembre 1915).
Il convient d’insister sur le fait que, si l’effet observé par GRAVITY est le même que celui étudié par Einstein dès 1915, le contexte est entièrement différent. La détection de l’effet de précession du péricentre dans l’environnement proche d’un trou noir supermassif est une validation beaucoup plus puissante de la théorie que cette même validation dans l’environnement solaire.
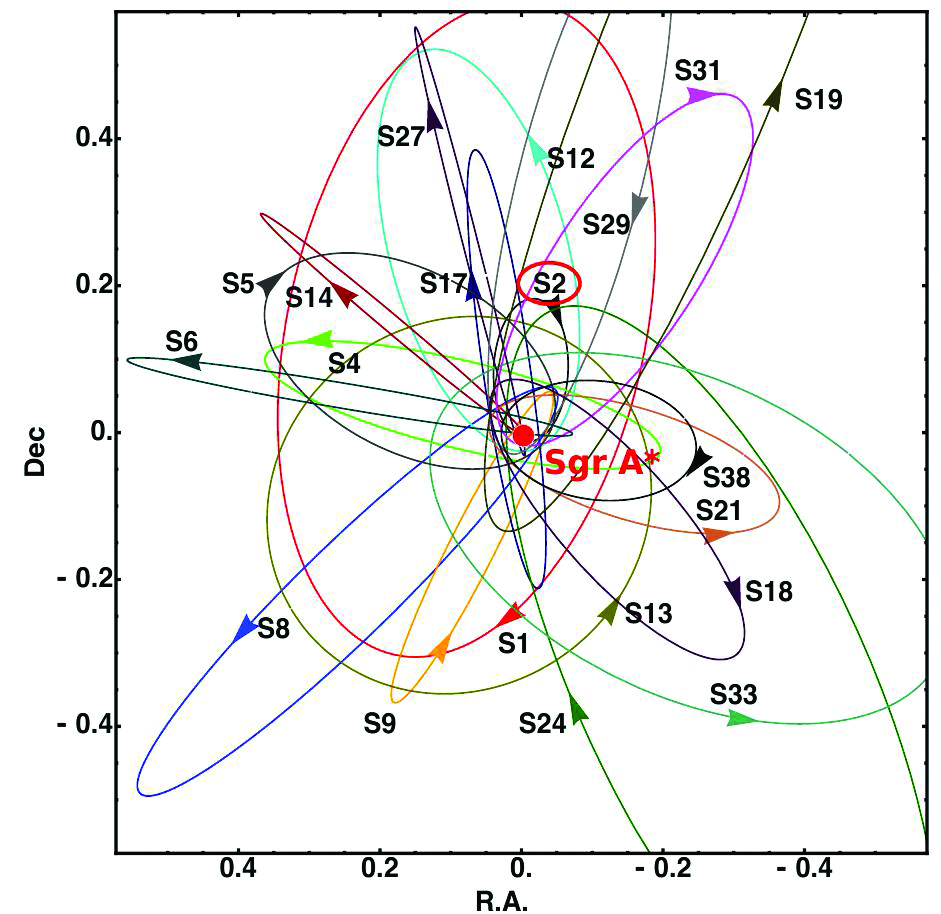
Figure 3 – L’amas d’étoiles situé autour du trou noir supermassif sgr A* au centre de la Galaxie. L’étoile s2 observée par Gravity, la plus proche du trou noir, est entourée en rouge. (Gillessen et al. ,2009)
En quoi consiste la détection par GRAVITY
La détection d’un mouvement de précession du péricentre nécessite à la fois un suivi sur le très long terme de l’étoile S2 (qui a une période orbitale de 15 ans), et une précision de mesure extrême au moment du passage au péricentre. La très longue base temporelle a été rendue possible par les observations continues de S2 effectuées depuis 2002 par la caméra infrarouge NACO du VLT. Les données GRAVITY ont quant à elles permis de suivre avec une précision fantastique le passage de S2 à son péricentre en mai 2018. C’est vraiment la combinaison de ces deux jeux de données (avec l’ajout des données spectroscopiques obtenues par l’instrument SINFONI du VLT) qui a permis une détection claire cette année.
Une fois les données orbitales enregistrées par NACO et GRAVITY, il a fallu ajuster un modèle théorique d’orbite à la trajectoire de S2. L’équipe GRAVITY a utilisé une approximation de la relativité générale, le formalisme post-Newtonien, qui permet de simplifier le problème tout en conservant une précision suffisante pour le cas traité ici. La Figure 4 montre le résultat crucial de l’article récent de la collaboration GRAVITY. Le modèle post-Newtonien ajuste parfaitement les données, alors qu’un modèle n’incluant pas la précession de Schwarzschild est exclu. Une étude statistique précise a permis de démontrer que la détection de la précession de Schwarzschild peut être considérée comme décisive.
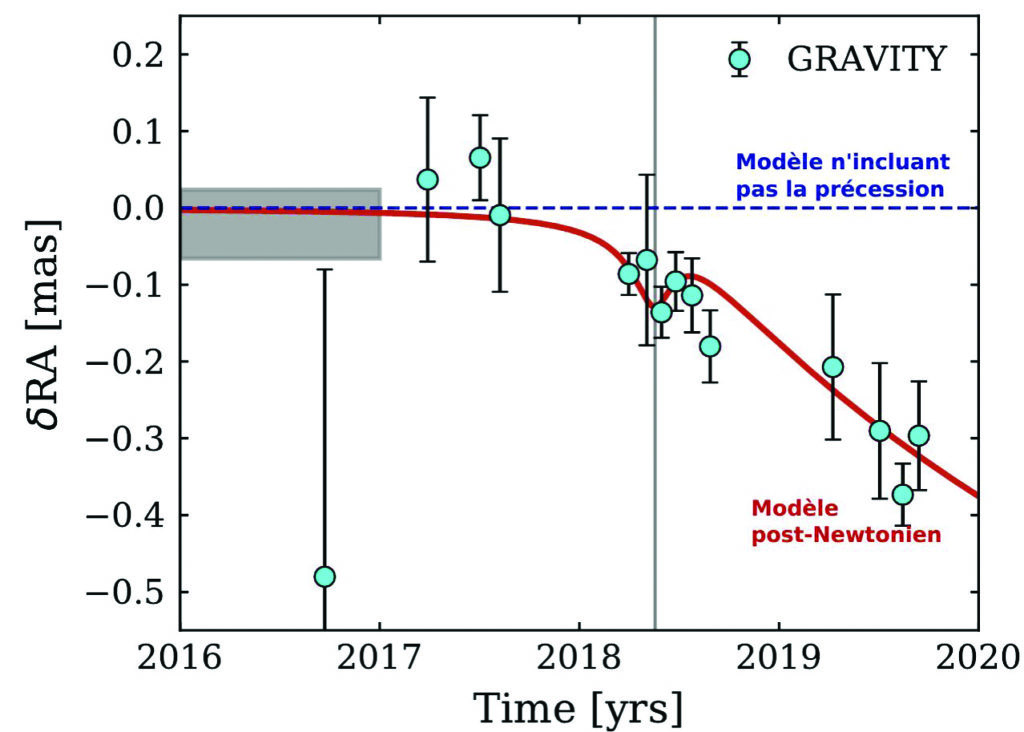
Figure 4 – Détection par Gravity de la précession de schwarzschild sur l’orbite de l’étoile s2. Les points de données en couleur cyan sont parfaitement ajustés par le modèle post- newtonien (approximation de la relativité générale complète, en rouge), alors qu’un modèle n’incluant pas la précession de schwarzschild (en bleu) est exclu. (Gravity collaboration, 2020)
De 1915 à 2020
Comme l’avait fait Einstein en 1915 pour Mercure, l’équipe GRAVITY a pu monter le parfait accord entre la prédiction de la relativité générale et la mesure de la précession de Schwarzschild de l’orbite de l’étoile S2. La Figure 5 compare une lettre d’Einstein portant sur son test de 1915 sur Mercure avec la formule de la précession de Schwarzschild utilisée dans l’article récent de la collaboration GRAVITY. C’est bien le même phénomène qui est étudié !
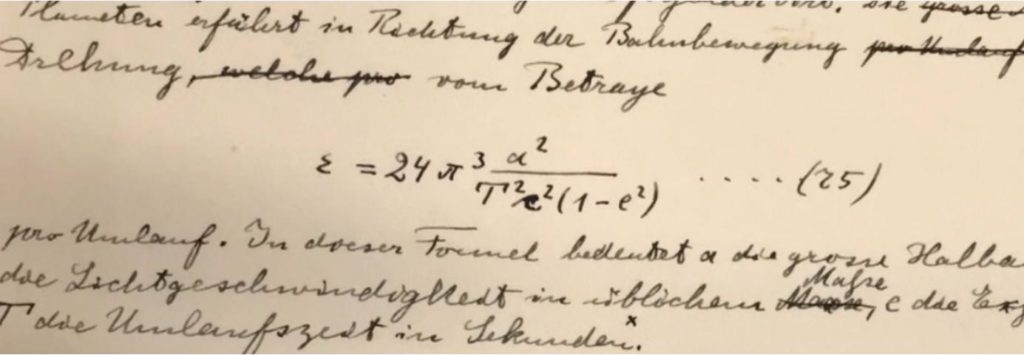
FIgure 5 – Texte d’einstein de 1915 relatif à la détection du mouvement de précession relativiste de mercure autour du soleil validant sa théorie. (en Médaillon) extrait de l’article de la collaboration Gravity mettant en évidence le même effet sur l’étoile s2 autour du trou noir supermassif au centre de notre Galaxie. Nous laissons à nos lecteurs les plus assidus le soin de montrer l’équivalence des deux formules.
Frédéric VINCENT | CNRS – Observatoire de Paris
