Le Soleil est une étoile magnétique, dont l’activité intense a un impact direct sur notre société moderne et technologique. Elle est actuellement modulée par un cycle d’activité de 11 ans. En a-t-il toujours été ainsi ? Cet état cyclique du magnétisme solaire perdurera-t-il au cours de son évolution ? Afin de répondre à ces questions clés concernant notre étoile, une équipe internationale, dont des chercheurs français, a mené à bien trois études sur l’origine du magnétisme et de la rotation du Soleil et des étoiles de type solaire (via le mécanisme physique dit de dynamo fluide) dans une approche « Soleil au cours du temps ».

Les grandes étapes de l’existence du Soleil
Le Soleil est passé par plusieurs phases au cours de sa vie. Tout a commencé au sein du milieu interstellaire (espace entre les étoiles au sein d’une galaxie) par l’effondrement gravitationnel (contraction sous sa propre masse à la suite d’une déstabilisation) d’un nuage de poussière et de gaz neutre (principalement du dihydrogène), appelé nuage moléculaire. Les mouvements présents au sein du nuage ont alors été amplifiés durant cette contraction originelle par conservation du moment cinétique : l’ensemble a acquis et amplifié sa rotation de la même façon qu’un patineur effectuant une pirouette accélère sa vitesse de rotation en rapprochant les bras de son corps [1] (fig. 2). Une fois que la densité a suffisamment augmenté, les forces de pression se sont opposées à l’effondrement, formant ce que l’on appelle une protoétoile (du grec protos signifiant « premier », « au début de ») et dont nous proposons de suivre l’évolution rotationnelle simplifiée sur la figure 1 :
– Couplage au disque : la rotation de la protoétoile est passée tout d’abord dans sa phase jeune par un plateau, c’est-à-dire un intervalle de temps où elle n’a pas varié. La rotation est demeurée constante sur plusieurs millions d’années tant que l’étoile ne se découplait pas de son disque de matière primordiale (ou disque d’accrétion). Ce dernier se forma autour d’elle par combinaison de la force gravitationnelle et de la force centrifuge durant la contraction du nuage.
– Fin de la contraction : une fois le disque d’accrétion dissipé (par exemple par sublimation ou par formation de planètes), la rotation de l’étoile a de nouveau accéléré par effet de la contraction toujours en cours (phase de pré-séquence principale ou PMS) pour atteindre les vitesses de rotation les plus élevées [2]. Une fois que les conditions de température et pression en son cœur furent suffisantes pour déclencher la fusion de l’hydrogène par réactions nucléaires, l’effondrement s’est arrêté et la protoétoile est devenue ce que l’on appelle communément une étoile. Ce point critique dans l’évolution stellaire s’appelle la ZAMS (zero age main sequence).
– Vers un lent ralentissement : l’étoile est alors entrée dans une phase, toujours actuelle, nommée séquence principale, où elle transforme son hydrogène en hélium. Cette phase durera 10 milliards d’années dans le cas du Soleil. Sa rotation ralentit maintenant, cette fois-ci par perte de moment cinétique via son vent de particules magnétisé. Ce scénario de l’histoire rotationnelle de notre étoile est confirmé par l’observation d’amas d’étoiles de différents âges, que nous représentons sur la figure 1 par les petits disques de couleurs avec barres d’erreur. En particulier, il a été proposé par Skumanich en 1972, puis Barnes en 2003, que le ralentissement des étoiles de type solaire suit une loi du type Ω(t) ~ t–1/2, laquelle implique qu’elles convergent toutes vers une même rotation à partir de l’âge des Hyades (soit environ 650 à 800 millions d’années). Cette relation directe entre âge et taux de rotation des étoiles de type solaire a été dénommée gyrochronologie (des mots grecs gyros, « rotation », chronos, « âge » et logos, « étude »).

Simulation 3D de la convection et de la dynamo d’une étoile semblable au Soleil pour comprendre l’évolution de la rotation interne et du magnétisme. En jaune/marron : vitesse radiale de la convection (montée/descente) ; en blanc : lignes de champ magnétique obtenues par extrapolation des valeurs en surface de la simulation. (A. Strugarek, Q. Noraz, A. S. Brun)
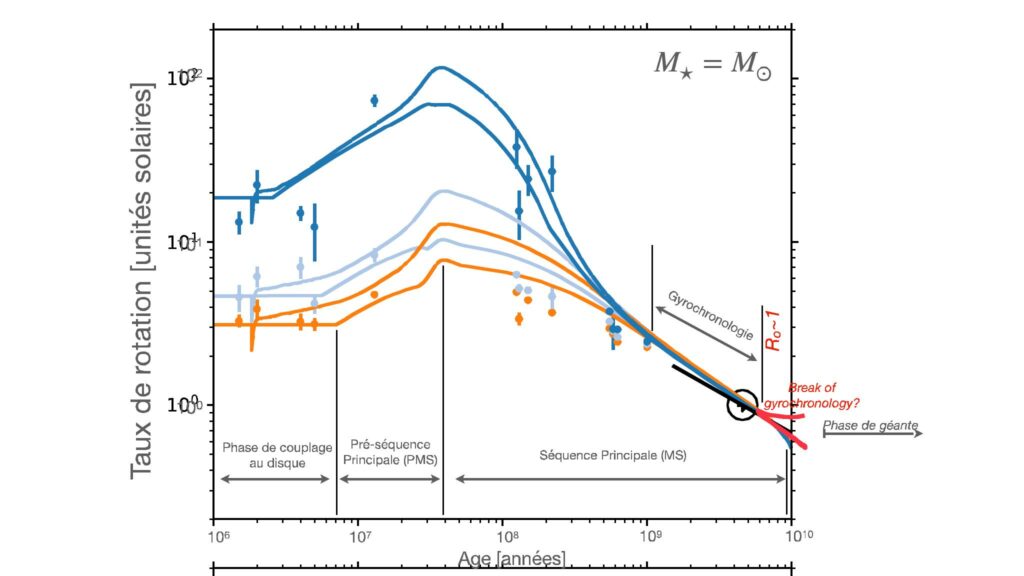
Figure 1. Évolution rotationnelle d’une étoile de 1 masse solaire sur les temps séculaires. Trois rotations initiales représentatives de la distribution observée dans les amas ouverts d’étoiles sont utilisées (rotateurs lents en orange, médians en bleu clair et rapides en bleu foncé). Les lignes solides représentent la rotation de l’enveloppe convective et celles pointillées de leur intérieur radiatif. Les petits cercles pleins avec barres d’erreur représentent les observations d’amas d’étoiles. Plusieurs phases rotationnelles sont identifiables : constante par ancrage à un disque de matière, en accélération par effet de contraction de l’étoile, puis décélération par freinage par vent magnétisé stellaire. La phase où toutes les courbes (quelle que soit leur vitesse initiale) convergent est la période évolutive où la gyrochronologie (la datation des étoiles par leur taux de rotation) est a priori possible, sauf si celle-ci s’arrête pour les étoiles âgées ayant un nombre de Rossby plus grand que 1 comme proposée récemment par certains auteurs. (Adapté de Ahuir et al., 2021)
La rotation non uniforme du Soleil
Cependant, la rotation globale d’une étoile de type solaire ne suffit pas à caractériser entièrement comment celle-ci tourne. En effet, le Soleil est constitué de plasma, qui est un état fluide de la matière [3]. Différentes parties de l’étoile peuvent alors avoir des mouvements indépendants les unes des autres, via une subtile redistribution de moment cinétique (nécessitant des simulations 3D pour leur étude et caractérisation), qui implique que tout ne tourne pas d’un bloc du centre à la surface. Ainsi, l’étoile présente un profil de rotation dite différentielle. Ces différentes vitesses s’organisent en fonction de la structure thermique de l’étoile, qui se décompose en deux grandes régions dans le cas du Soleil :
– L’intérieur radiatif : après que l’énergie thermique a été créée au centre par les réactions de fusion nucléaire, elle est évacuée vers la surface de l’étoile. Dans cet intérieur profond, la température et la densité sont très élevées et cela rend la matière transparente à la lumière : l’énergie thermique est alors principalement transportée par le rayonnement (c’est-à-dire par les photons)[4]. Cette zone est dite stable et possède une rotation dite « solide » : le taux de rotation est majoritairement constant, faisant tourner la zone interne radiative d’un seul bloc en 28 jours.
– L’enveloppe convective : à mesure que l’on s’éloigne du centre de l’étoile, l’opacité de la matière au rayonnement augmente, diminuant le libre parcours moyen [5] des photons, jusqu’à atteindre une localisation où les photons ne transportent plus l’intégralité de l’énergie thermique en direction de la surface. L’interaction des photons avec la matière dépose alors assez d’énergie pour modifier localement le gradient de température au point de déclencher l’instabilité convective. Le processus de convection transporte l’énergie thermique par mouvements macroscopiques de matière dans l’enveloppe externe du Soleil. À la manière d’une casserole d’eau frémissante lorsqu’elle est suffisamment chauffée par-dessous, la matière chaude monte jusqu’à la surface, tandis que la matière froide plus dense redescend. La zone convective du Soleil s’étend depuis la surface sur 30 % du rayon de l’étoile, mais cette profondeur change en considérant des étoiles de masses différentes. Cette enveloppe s’étend plus profondément pour les étoiles moins massives, tandis qu’elle est plus fine pour des étoiles plus massives, et disparaît totalement pour les étoiles dont la masse dépasse deux fois celle du Soleil. La convection redistribue le moment cinétique, et donc modifie les vitesses de rotation au sein de cette zone. Dans le cas du Soleil, on observe par exemple que la zone équatoriale tourne en 25 jours, tandis que les régions polaires tournent en 35 jours.
L’interface entre la zone radiative en rotation solide et la zone convective externe en rotation différentielle est ainsi une région où les vitesses de rotation changent fortement. Elle est nommée en ce sens tachocline (du grec táchos et klínô, signifiant « vitesse » et « inclinaison/pente ») et est visible sur le profil de rotation solaire illustré en figure 3.
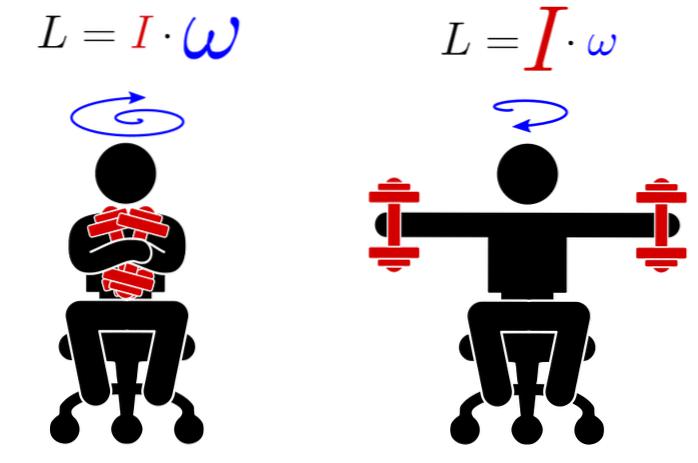
Figure 2. En considérant la conservation du moment cinétique L du système (humain + haltères), l’augmentation (la diminution) du moment d’inertie I, en écartant (regroupant) les bras, diminuera (augmentera) la vitesse angulaire de rotation w. (Source : fr.differbetween.com)
La production de champ magnétique grâce à la rotation différentielle
Cette rotation différentielle des étoiles favorise notamment la création d’un champ magnétique, grâce au processus de dynamo fluide. De manière similaire à une lampe alimentée par la dynamo d’un vélo, cette dernière permet de transformer l’énergie mécanique en énergie électromagnétique. Dans une étoile, ce processus dynamo fluide est la propriété que possède un plasma de générer par ses mouvements et par auto-induction un champ magnétique et de le maintenir. En effet, s’il n’est pas entretenu, le champ magnétique décroît : les courants électriques de la dynamo, intimement liés au champ magnétique, se dissipent en produisant de la chaleur, comme dans n’importe quel conducteur électrique résistif. On parle de dissipation du champ magnétique par diffusion ohmique. Seuls certains écoulements peuvent amplifier et maintenir un champ magnétique contre sa diffusion naturelle, ce qui est le cas des écoulements turbulents au sein du Soleil. En effet, l’association de la convection turbulente et de la rotation différentielle confère au plasma des propriétés d’étirement, de cisaillement et d’enroulement nécessaires à la mise en place de la dynamo fluide.
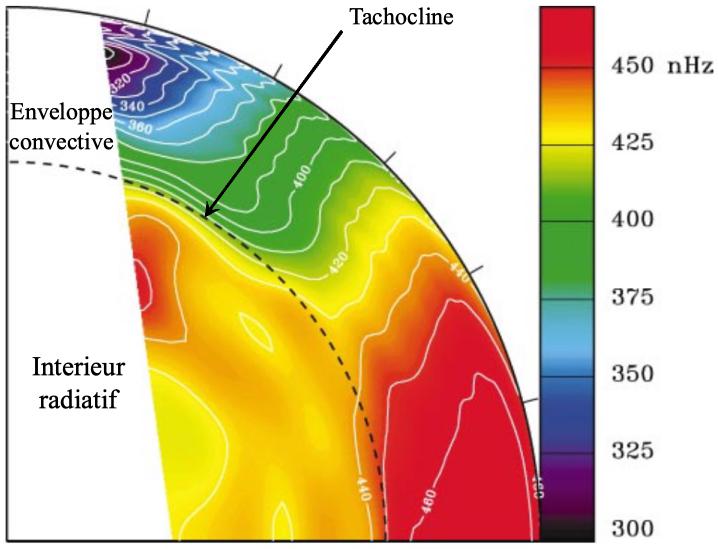
Figure 3. Rotation différentielle du Soleil. Coupe méridienne du profil de rotation de l’hémisphère Nord solaire. On y remarque la rotation solide de l’intérieur radiatif en jaune (28 jours), séparé par la tachocline (en pointillé) de l’enveloppe convective en rotation différentielle. La partie équatoriale de cette dernière (en rouge) est plus rapide (~25 jours) que celle de la région polaire (en violet/noir), pouvant ralentir jusqu’à 38 jours. Source : Thompson et al. (2003).
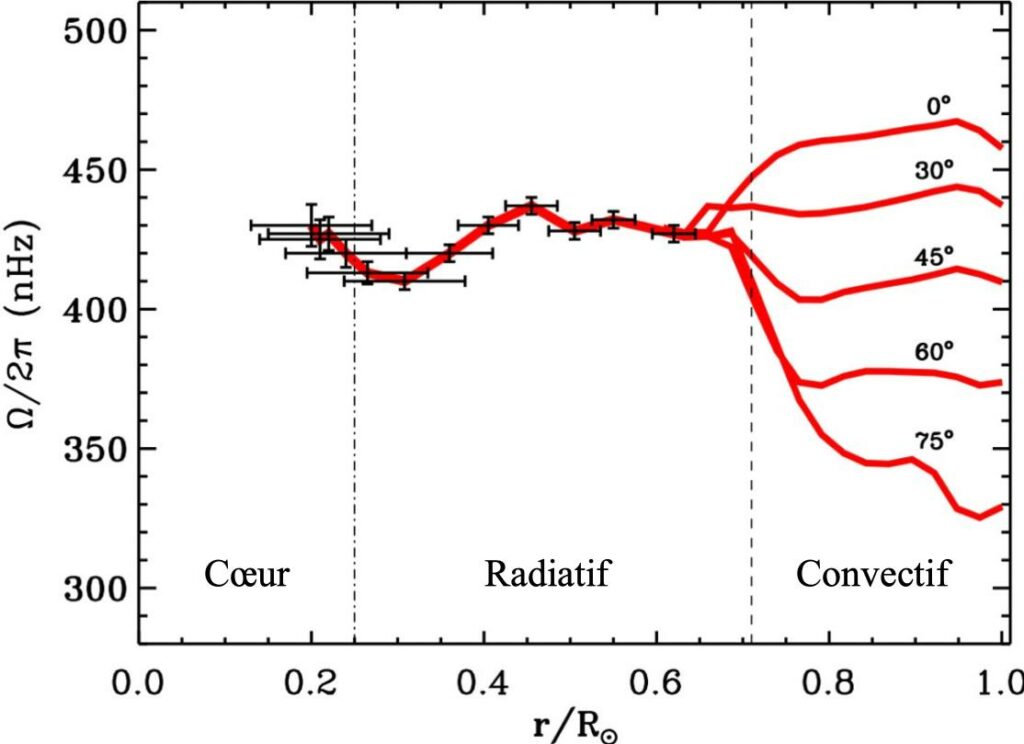
Profils radiaux de cette même rotation pour des latitudes particulières (0, 30, 45, 60 et 75°). On remarque le regroupement des différentes courbes, représentant le passage de la rotation différentielle à la rotation solide, et définissant la « tachocline ». (Garcia et al., 2007)
Pour décrire le champ magnétique d’une étoile, les chercheurs ont l’habitude de l’illustrer par l’intermédiaire de lignes de champ magnétique : lignes imaginaires illustrées en figures 4 et 5, indiquant le sens et l’intensité du champ magnétique et le long desquelles se déplacent en s’enroulant (mouvement dit « giratoire ») les particules chargées. On voit en figure 4 le champ magnétique représenté en deux composantes, usuellement utilisées pour le décomposer mathématiquement et l’étudier. La première est la composante dite poloïdale, contenue dans le plan de l’étoile passant par les deux pôles (plan méridien) et comparable à la géométrie des aimants que nous utilisons au quotidien (voir figure 5). La seconde est nommée composante toroïdale, en référence à la forme de « tore/donut » que prend cette dernière, et qui est contenue dans le plan perpendiculaire à l’axe de rotation. La géométrie globale du champ magnétique peut varier selon les étoiles. En particulier, elle structure et guide la couronne solaire, et par conséquent l’éjection de particules chargées, à l’origine du « vent » stellaire magnétisé visible sur la figure 4.
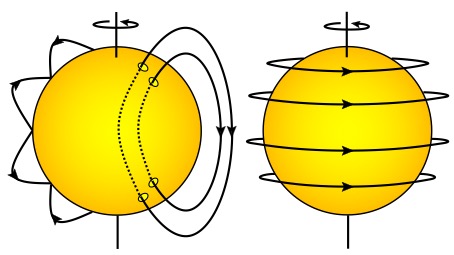
Figure 4. Composantes usuellement utilisées pour décrire le champ magnétique stellaire à grande échelle. À gauche : composante dite
« poloïdale », contenue dans le plan méridien de l’étoile. Le côté droit de l’étoile représente la composante dipolaire (une boucle à grande échelle), tandis que le côté gauche représente une composante multi- polaire (ici la composante hexadécapolaire avec les 4 boucles).
À droite : composante dite « toroïdale », contenue dans le plan perpendiculaire à l’axe de rotation.
Le vent solaire et le ralentissement de la rotation
Au travers de ce vent, l’étoile perd de la masse et donc du moment cinétique. En effet, de façon similaire au patineur écartant ses bras pour ralentir la rotation de sa pirouette, ce vent magnétisé génère un effet de bras de levier. L’amplitude de ce couple dépend notamment de l’intensité et de la géométrie du champ magnétique créé, et abaisse progressivement le taux de rotation de l’étoile, comme nous le voyons en figure 1. Une rotation plus rapide a tendance à générer un champ magnétique plus intense, et donc un freinage par vent magnétisé d’autant plus important (courbe bleu foncé). À l’inverse, une rotation plus faible est à l’origine d’un champ généralement moins intense, il est donc impacté par un freinage plus faible (courbe orange). Cette boucle de rétroaction « rotation -> dynamo -> magnétisme -> vent -> freinage -> rotation » est à l’origine de la convergence des étoiles de même masse (ici une masse solaire) vers la loi de Skumanich Ω(t) ~ t–1/2, et permet ainsi la gyrochronologie.

Figure 5. Illustration du champ magnétique d’un aimant usuel en utilisant de la limaille de fer. Cette limaille est alors orientée par le magnétisme, en traçant les « lignes de champ ». (Newton Henry Black, Practical Physics, 1913)
Les cycles d’activité du Soleil ont-ils toujours existé ?
Ainsi, pendant que la rotation de l’étoile diminuait sur des durées de l’ordre du milliard d’années, l’intensité globale du champ magnétique en faisait généralement de même. Cependant, la dynamo fluide a pu parfois conduire à des variabilités cycliques de l’intensité et l’orientation de ce champ sur des temps bien plus courts ! De tels changements de polarité et d’intensité ont tout d’abord pu être mis en évidence pour la dynamo terrestre, avec des traces d’inversions passées des pôles magnétiques, observées dans l’aimantation de certaines roches volcaniques et illustrées en figure 6 (lire l’encadré 2 et la note [6]).
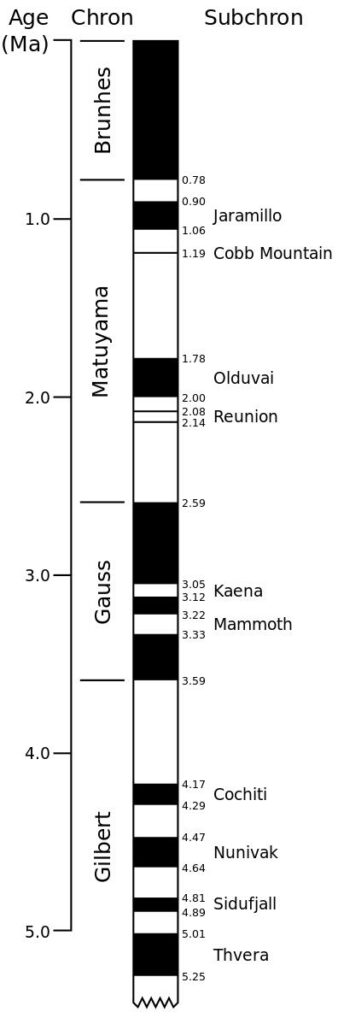
Figure 6. Polarité géomagnétique pendant la fin de l’ère cénozoïque (de –5 millions d’années à nos jours). Les zones sombres indiquent les périodes de polarité dite « normale », tandis que les zones claires indiquent une polarité « inverse ». Les transitions noir/blanc correspondent donc au renversement global de la composante poloïdale (voir figure 4) du champ magnétique terrestre. On remarque que le dernier renversement remonte à 780 000 ans. (U.S. Geological Survey Open-File Report 03-187)
Sur le Soleil, des inversions similaires de l’orientation magnétique globale (dite « polarité ») sont observées de manière cyclique tous les 11 ans, et sont illustrées en figure 7 (sur la figure 4, leur effet revient à inverser le sens des flèches). On observe aussi durant ces cycles un changement de la fréquence d’apparition des structures magnétiques à sa surface, les tâches solaires, dont le nombre atteint son maximum tous les 11 ans. On parle de « maximums d’activité », et ceux-ci sont séparés par des « minimums d’activité » pendant lesquels ces structures sont absentes de la surface. Le dernier minimum solaire est survenu en décembre 2019, date depuis laquelle l’activité repart à la hausse, et atteindra un prochain pic, attendu autour de 2025. Des traces de cycles magnétiques ont également été détectées pour d’autres étoiles de type solaire, allant de quelques années à quelques dizaines d’années. Il est alors important de comprendre comment ces cycles sont contrôlés dans leur ensemble, afin de mieux comprendre l’activité du Soleil et l’impact qu’elle pourrait avoir sur nos sociétés technologiques. En effet, rappelons que la Terre baigne dans la lointaine atmosphère du Soleil, laquelle est turbulente et magnétique.
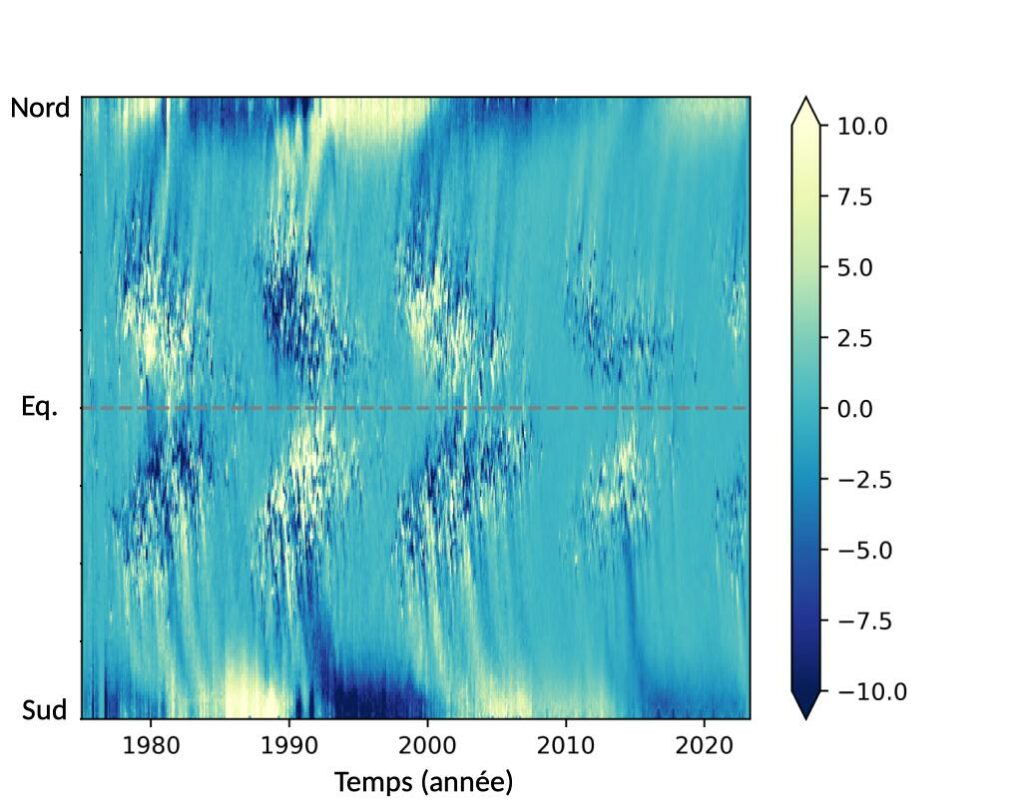
Figure 7. « Diagrammes papillon » du Soleil de 1976 à 2022. Il s’agit d’une représentation temps-latitude du champ magnétique de surface. La couleur blanc/bleu représente un champ pointant vers l’extérieur/l’intérieur du Soleil (une polarité positive/négative), mesuré ici en gauss (10 000 gauss = 1 tesla). Nous voyons différents maximums d’activité en 1981, 1991, 2000 et 2012, dessinant des formes d’ailes, et séparés par les minimums d’activité de 1976, 1986, 1996, 2008 et 2019. (Construit à partir des données KPNO, GONG, SOLIS & MDI)
Ainsi, allant de pair avec le changement du taux de rotation de l’étoile, le niveau d’activité magnétique de l’étoile est lui aussi modifié au cours de sa vie. On observe en effet que les étoiles jeunes tournent rapidement et sont très actives, tandis que les plus vieilles semblent moins actives et plus lentes. Cependant, la gyrochronologie a possiblement été remise en cause par les données du satellite Kepler (van Saders et al. 2016). Comme illustré en figure 1, le freinage des étoiles de type solaire s’arrêterait vers l’âge du Soleil (environ 4,5 milliards d’années), ce qui signifie que le vent ne serait plus aussi efficace pour extraire le moment cinétique des étoiles âgées. Cela pourrait s’expliquer par exemple par un changement de géométrie globale du champ magnétique solaire/stellaire, ou une modification de leur perte de masse. Il faut donc mieux caractériser la boucle complexe de rétroaction « dynamo -> magnétisme -> vent -> freinage -> rotation -> dynamo » pour comprendre l’évolution séculaire du magnétisme des étoiles de type solaire, et la possible existence d’un changement de régime magnéto-rotationnel.
Un nombre clé pour caractériser l’évolution de la rotation et du magnétisme solaires
En ce sens, il a récemment été montré que ces changements de régimes peuvent être délimités via une quantité appelée nombre de Rossby « Ro » (lire l’encadré 3). Ce nombre permet de caractériser comment la rotation globale d’une étoile influence sa dynamique convective interne. À masse équivalente, les étoiles jeunes en rotation rapide auront un nombre de Rossby plus faible, tandis que les étoiles plus âgées tournant lentement auront un nombre de Rossby plus élevé. Si l’on regarde maintenant des étoiles de masses différentes, une étoile aura un nombre de Rossby d’autant plus élevé qu’elle est massive.
Grâce à des simulations numériques menées sur les supercalculateurs situés dans les centres français, une équipe de chercheurs français accompagnés de collègues internationaux a développé des simulations de la dynamo des étoiles de type solaire avec ce but précis (résultats publiés dans Brun et al., 2022). En changeant la masse et la rotation, et donc le nombre de Rossby des étoiles simulées (au nombre de 15), ils ont pu explorer différents états de rotation interne de l’étoile, et par conséquent de son magnétisme.
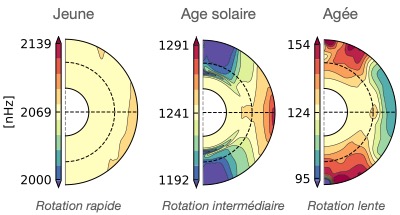
Figure 8. Profils de rotation dans une coupe méridienne de trois simulations dynamos convectives 3D d’une étoile de type solaire à différents taux de rotation globale (nombres de Rossby Ro : Ro < 0,2 (gauche), Ro ~0,2-0,7, Ro > 1 (droite)). Les régions rouges représentent un taux de rotation plus grand que la rotation globale (jaune pâle), tandis que les régions bleues représentent des taux de rotation plus faibles. (Adapté de Noraz et al., 2022b)
Pour illustrer cela, nous montrons sur la figure 8 trois états de rotation caractéristiques de l’étude :
– Un état de rotation quasi solide pour les rotateurs rapides : Ro faible – étoile jeunes.
– Un état de rotation dit solaire, avec un équateur rapide et des pôles lents : Ro et âges intermédiaires. Il est caractéristique du Soleil, mais aussi d’étoiles comme Ɛ Eridani ou 61 Cygni A.
– Un état de rotation dit antisolaire, avec des pôles rapides et un équateur lent : Ro élevé – étoiles potentiellement âgées. De tels profils ont déjà été détectés pour des étoiles géantes rouges, mais restent à confirmer pour des étoiles de type solaire.
Certains profils de rotation favorisent les cycles d’activité magnétique, d’autres pas
Ce changement de profil de rotation interne affecte alors directement le comportement de la dynamo, certaines dynamos présentant alors des cycles et d’autres non. Sur la figure 9, nous montrons un diagramme de synthèse de l’état magnétique des étoiles selon leur nombre de Rossby, obtenu grâce à l’étude paramétrique publiée en 2022. On peut remarquer trois grandes classes :
– des dynamos cycliques à période courte (< 2 ans) pour les petits nombres de Rossby (en haut) ;
– des cycles longs pour les nombres de Rossby intermédiaires similaires au Soleil (au milieu) ;
– et enfin des dynamos sans cycle (« stationnaires ») pour les nombres de Rossby supérieurs à 1 (en bas).

Figure 9. « Diagrammes papillon » simulés pour les 3 types de dynamos. Il s’agit d’une représentation temps- latitude des polarités du champ magnétique poloïdal (en haut) et toroïdal (au milieu et en bas). La couleur rouge/bleu représente une polarité positive/négative. Trois cas de dynamos sont ainsi illustrés, soit avec un cycle magnétique court pour les plus faibles Ro (en haut), un cycle long de type solaire (au milieu) et sans cycle (en bas) pour les Ro les plus élevés. (Adapté de Brun et al., 2022)
« Antisolaire » : les étoiles dont le pôle tourne plus vite que l’équateur
Il semblerait donc que pour les rotateurs lents, un état de rotation antisolaire amène bien à la perte du cycle de la dynamo, qui devient alors stationnaire. Afin de confirmer cet état stationnaire dans le cas d‘une rotation antisolaire, l’équipe de chercheurs a entrepris une étude spécifique des dynamos antisolaires (publiée dans Noraz et al. 2022a), à partir d’un modèle à 2 dimensions réduit, mais plus rapide en temps de calcul, afin d’étendre l’espace des paramètres couverts.
Une partie de cette étude est résumée dans la figure 10, où sont illustrés différents chemins pour la boucle dynamo. Les conclusions confirment, comme dans le cas des simulations 3D, que les profils de rotation antisolaire donnent en majorité des dynamos sans cycle. Dans le cas solaire (ligne du bas #3), la boucle dynamo annule et renverse le champ aux pôles. On voit que les flèches du champ poloïdal se sont renversées entre la première et la dernière image de la rangée (dirigées vers le haut initialement, puis vers le bas finalement). Dans le cas antisolaire (ligne du haut #1), la boucle dynamo renforce au contraire, dans la plupart des cas, le champ aux pôles, et les flèches du champ poloïdal ne se renversent alors pas (elles restent orientées vers le haut). Néanmoins, des cycles magnétiques restent possibles avec rotations antisolaires, pour des modèles de dynamo spécifiques (ligne du milieu #2). Une détection de cycles magnétiques pour de telles étoiles (ou l’absence de cycles) serait donc une contrainte énorme pour différencier quel type de dynamo agit réellement au sein du Soleil, et prédire comment celui-ci évoluera. En attendant, il semble donc que les rotateurs lents aient une réelle probabilité d’avoir un magnétisme non cyclique.

Figure 10. Différents chemins possibles pour une dynamo stellaire. L’effet dit Ω à gauche, transforme les lignes de champ magnétique poloïdales (voir figure 4) en champ toroïdal par la rotation différentielle (cisaillement grande échelle). Son sens dépend du type de profil de rotation (solaire ou antisolaire). L’effet-α, à droite, permet de représenter l’impact de la convection hélicoïdale, transformant à l’inverse les lignes de champ toroïdales en composante poloïdale. En bas #3 : cas de référence solaire où la polarité magnétique globale est inversée à la fin de la boucle (dynamo AC). En haut #1 : cas de référence antisolaire où le cisaillement Ω est inversé, tout en considérant une paramétrisation α similaire. Cela conduit à une dynamo stationnaire sans cycle (dynamo DC). Au milieu #2 : cas antisolaire où le sens de l’effet-α est inversé, considérant alors le changement de nature de la convection à la base de l’enveloppe convective (passage d’un mouvement cyclonique à anticyclonique dans l’hémisphère Nord, et inversement pour l’hémisphère Sud). Ce cas très particulier conduit à une solution cyclique, comme dans le cas solaire. (Adapté de Noraz et al., 2022a).
Cela veut-il dire pour autant que la géométrie magnétique globale principale de la simulation a changé ? Par exemple, passant de la domination d’un dipôle grande échelle (structures poloïdales de droite, schématisées en haut à gauche de la figure 4) à une structure de champ magnétique petites échelles, dite multipolaire (structures poloïdales de gauche schématisées en figure 4) ? Si tel était le cas, l’efficacité du freinage de la rotation par le vent en serait fortement réduite, car la taille du bras de levier appliqué par le champ magnétique le serait tout autant. Quand l’équipe de chercheurs étudie la géométrie magnétique globale des dynamos antisolaires et la compare aux rotateurs rapides, elle ne remarque cependant pas de changement flagrant de l’amplitude du dipôle (ou des autres composantes grandes échelles du champ magnétique). En effet, la figure 11 représente l’amplitude du dipôle dans les 15 simulations en fonction du nombre de Rossby, et la compare aux observations astronomiques. On remarque bien que, pour les Ro < 1, l’accord entre simulations et observations (courbes violette et noire) est très bon, confortant les auteurs que les simulations sont robustes et réalistes.
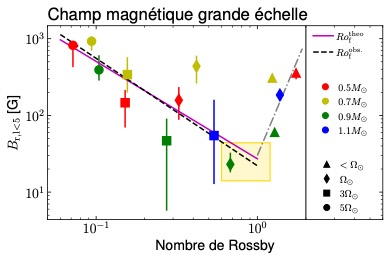
Figure 11. Amplitude du champ magnétique à grande échelle en fonction du nombre de Rossby dans les 15 simulations de dynamo convective stellaire. Les différentes couleurs/formes représentent les différentes masses/taux de rotation des étoiles simulées (exprimées en unité solaire ☉). Les barres reliées aux points représentent l’amplitude de variation de ce champ à grande échelle, qui peut être forte pour les cas à dynamo cycliques. Enfin, les courbes violette et noire représentent la tendance des simulations/observations pour Ro < 1. Le carré jaune pâle représente un possible minimum magnétique où certaines étoiles pourraient être piégées un certain temps, s’écartant ainsi de la relation classique rotation-âge (ou gyrochronologie). (Adapté de Brun et al., 2022)
A contrario, quand on considère les cas à Ro > 1, on remarque que l’amplitude de ceux-ci ne suit pas la même tendance, ni même une baisse encore plus abrupte de l’amplitude du dipôle. Bien au contraire, on voit une possible remontée du champ magnétique dipolaire. Le dipôle magnétique de la dynamo stationnaire au sein des rotateurs lents n’est donc pas négligeable ; au contraire, il semble même dominant. Dès lors, il semble peu probable que ce soit la disparition du dipôle magnétique qui mette en pause le ralentissement des étoiles suggéré par l’étude Kepler citée plus haut. Il est cependant intéressant de noter sur la figure 11 l’existence possible d’un minimum local du champ magnétique grande échelle vers l’âge du Soleil, indiqué par la petite boîte jaune. On peut donc se poser la question de savoir si des étoiles pourraient y rester « coincées », expliquant ainsi leur inefficacité à ralentir selon la loi de Skumanich en Ω(t) ~ t–1/2 (c.-à-d. la rotation de l’étoile ralentit comme l’inverse de la racine carrée du temps : plus l’étoile est âgée, moins elle tourne vite sur elle-même). Mais une fois ce minimum passé, les étoiles retrouvent a priori un freinage plus intense. La durée de cette phase de « calage/décrochage » (stalling en anglais) dépend de la forme du minimum, soit pour faire simple en forme de U ou de V. Cela peut avoir des conséquences sur l’âge des étoiles vieilles auquel on devrait ajouter cette période de stalling, pour corriger la gyrochronologie.
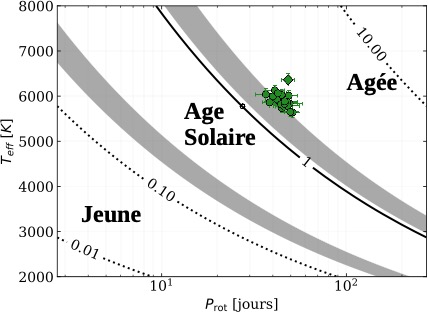
Figure 12. Représentation des étoiles candidates au profil antisolaire dans les observations Kepler, après filtrage et diagnostic en nombre de Rossby. On y retrouve notamment KIC 7189915, une étoile très similaire au Soleil, ainsi que KIC 12117868, une cible intéressante pour l’astéro-sismologie. (Adapté de Noraz et al., 2022b)
Dans ce contexte, l’équipe de chercheurs a entrepris l’identification d’étoiles candidates dans les données du satellite Kepler, dont le profil de rotation pourrait être antisolaire, afin de confirmer dans cette première étape l’existence de ce profil dans les vieilles étoiles de type solaire (Noraz et al., 2022b). La figure 12 représente ainsi un diagramme de la température de surface (effective) en fonction de la période de rotation en jour. Les étoiles de l’échantillon Kepler ayant un grand nombre de Rossby observationnel, et donc susceptibles de posséder une rotation antisolaire, sont marqués d’un symbole vert. Il s’agira maintenant de dédier un programme d’observations pour vérifier leur possible profil de rotation inversé, mais aussi pour caractériser leur champ magnétique. Cela nous apportera alors des informations sur la forme exacte du minimum de la figure 11, et donc sur le potentiel écart à la gyrochronologie illustré en figure 1. Cela permettra enfin de suivre leur activité magnétique sur le long terme, afin de savoir si elle est stationnaire ou cyclique.
Ce scénario magnéto-rotationnel des étoiles guidera en partie la mission spatiale de l’ESA PLATO pour lequel la France est fortement impliquée. En effet, la compréhension du magnétisme et de ses variabilités améliore la détection d’exoplanètes, souvent perturbée par l’activité magnétique de l’étoile hôte. L’étude sur le magnétisme des étoiles permet non seulement de reconstruire leur histoire magnéto-rotationnelle, mais peut également aider à mieux caractériser les nombreuses exoplanètes présentes dans notre environnement proche, et ainsi mieux contraindre nos connaissances sur les possibilités de vie au sein de notre Galaxie.
Par Quentin NORAZ, Allan Sacha BRUN & Antoine STRUGAREK, DAp-AIM/OSUPS

Publié dans le magazine L’Astronomie Juin 2023
Notes :
- Le moment cinétique est une grandeur utilisée pour décrire l’état général de rotation d’un système physique. Ainsi, comme la quantité de mouvement (« l’élan ») d’un système en translation uniforme ne sera pas modifiée si aucune force nette ne lui est appliquée (3e loi de Newton : principe d’inertie), le moment cinétique d’un système en rotation n’est pas modifié si aucun couple ne lui est appliqué. En considérant une conservation de cette grandeur, la vitesse de rotation peut être modifiée de façon caractéristique si la répartition des masses autour de l’axe de rotation l’est aussi (voir l’exemple de la pirouette du patineur et illustration en figure 2).
- La sublimation est le changement d’état d’un corps depuis l’état solide vers l’état gazeux, sans passer par l’état liquide.
- Le plasma est considéré comme le quatrième état de la matière, en plus de solide, liquide et gazeux. Il s’agit plus exactement d’un gaz ionisé, c’est-à-dire au sein duquel les électrons ont assez d’énergie pour se séparer des atomes. Au sein du Soleil, cet état est atteint grâce aux conditions extrêmes de température en son sein, allant de quelques milliers de degrés à sa surface, jusqu’à plusieurs millions en son centre.
- Le transport de l’énergie thermique par conduction (contact direct entre un corps chaud et un corps froid) est négligeable au sein des étoiles de type solaire.
- Le libre parcours moyen est la distance moyenne parcourue par une particule ou un photon, entre deux impacts successifs.
- Lorsque la croûte terrestre se forme au niveau d’une dorsale océanique par remontée de magma, certaines roches de ce dernier enregistrent l’aimantation globale présente lors de leur solidification. Les mouvements tectoniques engendrés vont alors éloigner progressivement ces roches de la dorsale par formation de nouvelles roches plus récentes, et permettent ainsi de remonter l’histoire du champ magnétique terrestre à mesure que l’on regarde des roches de plus en plus éloignées de la dorsale.
Références :
■ Noraz Q., Breton S. N., Brun A. S., García R. A., Strugarek A., Santos A. R. G., Mathur S., Amard L., 2022, Astronomy & Astrophysics, 667, A50, 2022.
■ Brun A. S., Strugarek A., Noraz Q., Perri B., Varela J., Augustson K., Charbonneau P., Toomre J., 2022, Astrophysical Journal, 926, 21, 2022.
■ Noraz Q., Brun A. S., Strugarek A., Depambour G., Astronomy & Astrophysics, 658, A144, 2022.
■ Ahuir J., Strugarek A., Brun A.-S., Mathis S., Astronomy & Astrophysics, 650, A126, 2021.
■ Strugarek A. et al., Science, 357, 185, 2017.
■ Van Saders J. L. et al., Nature , 529, 2016.
■ Thompson M. J. et al., « The Internal Rotation of the Sun », Annual Review of Astronomy and Astrophysics, 41, 2003, 599.
■ Garcia R. A. et al., « Tracking Solar Gravity Modes: The Dynamics of the Solar Core », Science, 316, 2007, 1591.
■ Monchaux R. et al., Physics of Fluids 21, 035108, 2009.
■ C. M. Cooper et al., Physics of Plasmas 21, 013505, 2014.
■ Newton Henry Black, Practical Physics, 1913.
