Introduction
La théorie de la gravitation d’Einstein, appelée également Relativité Générale, a fait l’objet d’une intense couverture médiatique ces dernières années. En effet, il y a eu tout d’abord le centenaire de la première publication de la théorie complète publiée par Einstein en novembre 1915, puis la détection des ondes gravitationnelles en septembre 2015 et annoncée le 11 février 2016, qui apportait en même temps la première preuve sérieuse de l’existence des trous noirs. Par la suite, nous avons eu le centenaire de cette fameuse observation de la déflexion de la lumière par le Soleil lors de l’éclipse de 1919 dont il sera question dans cet article. Enfin, plus récemment, trois prix Nobel de physique sont directement en lien avec la Relativité Générale, tout d’abord en 2017 pour le développement des détecteurs d’ondes gravitationnelles et leur observation, en 2019 pour les découvertes théoriques en cosmologie physique et enfin en 2020 pour les trous noirs. Cela fait beaucoup pour une théorie, développée par un seul homme, en quelques années, sans que ce soit en réponse à une crise ou l’aboutissement d’un long processus collectif d’avancées successives plus ou moins erratiques : la théorie est née du cerveau d’un seul homme, quasiment sous sa forme finale en novembre 1915, et n’a pratiquement pas été altérée depuis. Cela contraste avec la lente émergence de la mécanique quantique, l’autre pilier de la physique moderne, fruit de décennies de travaux sur l’électron, les atomes, le rayonnement et dont les principes fondamentaux font encore l’objet d’âpres discussions sans que cela ne remette en cause ses succès extraordinaires.
Ce texte a pour but de revenir sur l’éclipse solaire de 1919, sur le rôle de Sir Arthur Eddington dans la mesure de la position des étoiles durant l’éclipse totale et par la suite la confirmation quantitative de la prédiction d’Einstein, par opposition à celle déduite d’une application (hasardeuse ou audacieuse selon les cas) de la théorie Newtonienne à la lumière. Ce sujet a fait l’objet de multiples publications, d’ouvrages entiers même, et de controverses non dénuées d’arrières plans politiques. Ce texte n’en est qu’un simple résumé et ne prétend à aucune originalité dans son contenu. Il aura le mérite, je l’espère, de montrer qu’un résultat scientifique n’est pas noir ou blanc, et que, s’il n’est pas répété, confirmé, amplement discuté et validé, il ne peut à lui seul faire basculer une théorie.
Contexte
La possibilité d’une déviation gravitationnelle du trajet de la lumière n’émerge pas du jour au lendemain avec la publication de la théorie de la gravitation par Albert Einstein en novembre 1915 et mai 1916. Lui-même a tout d’abord abordé cette question dès 1907 comme conséquence du principe d’équivalence. Les calculs menés entre 1907 et la découverte des équations du champ de la théorie en 1915, donnaient une déviation conforme au calcul newtonien, c’est à dire ce que l’on obtiendrait en appliquant la mécanique Newtonienne à une particule passant au bord du Soleil avec la vitesse de la Lumière. Comme les effets gravitationnels ne dépendent pas de la masse du corps influencé, on peut effectuer ces calculs sur une particule de masse quelconque, par exemple en attribuant au photon un masse proportionnelle à son énergie. On trouve alors que la déviation pour un rayon lumineux passant à la distance de la terre du centre du Soleil serait de 0,85 seconde d’arc (un angle d’une seconde d’arc vaut 1/3600ème de degré). Un angle extrêmement faible, dont Einstein doutait de la possibilité de le mesurer, bien qu’il eût déjà songé que la seule méthode envisageable était d’observer les étoiles durant une éclipse totale. Il va d’ailleurs pousser des astronomes de Berlin à entreprendre cette tâche.
La trajectoire de la lumière des étoiles passe au-plus près du Soleil et, pendant l’éclipse, il est possible de les voir, au moins sur une plaque photographique. C’est donc une configuration optimale pour l’observation optique, avec la condition supplémentaire d’avoir quelques étoiles brillantes dans le voisinage solaire. En comparant leurs positions relatives avec celles enregistrées dans des conditions normales, ou bien à partir de positions cataloguées, il est en principe possible de tester la prédiction. Mais au-delà du principe élémentaire, et comme souvent en astronomie, la réalité se heurte à la faiblesse du signal par rapport aux effets systématiques et aux erreurs aléatoires. Nous sommes au début du XXe siècle, et l’astronomie de position à la seconde de degré n’est pas le quotidien des astronomes.
Avant d’en venir à la prévision finale de la Relativité Générale, notons dès maintenant qu’Einstein n’est pas le premier à faire ce calcul et cette prédiction. Tout d’abord l’influence possible de la gravitation sur la lumière a été anticipée par le Révérend J. Michell (1724-1793) en 1785, dans un tout autre cadre, mais qui se trouve être en relation avec une autre prédiction de la théorie d’Einstein. Il s’est demandé ce que ferait la lumière émise à la surface d’une étoile si sa masse était telle que la vitesse de libération devenait plus élevée que la vitesse de la lumière. Son avis était que la lumière ne pourrait échapper à la force d’attraction et en conséquence que l’étoile resterait invisible. Chacun a compris qu’il s’agit là d’une anticipation du phénomène de trou noir dans son expression la plus élémentaire. Son calcul était parfaitement correct et le rayon donné correspond au rayon de Schwarzschild pour un objet de la densité du Soleil, mais dont le rayon serait 497 fois sa valeur actuelle. Cette même idée a été brillamment reprise par P.S Laplace dans son Exposé du Système du Monde et la notoriété de l’auteur a contribué à sa diffusion.

Figure 1: Effet de la gravité sur la lumière chez le Révérend J. Michell en 1784. Le texte décrit le cas où la vitesse de libération d’une étoile égale la vitesse de la lumière.
Encore plus proche du problème soulevé par Einstein, est le calcul effectué en 1801 et publié en 1804 par l’astronome allemand Johann Georg von Soldner (1776-1833) dans le cadre de la théorie corpusculaire. Le calcul aboutit au résultat classique de la déflexion en physique newtonienne. En conclusion il mentionne, non pas la détection de l’effet par l’observation, mais la contrainte que cela ferait peser sur des observations d’astronomie de position lors d’une observation hypothétique d’étoiles proches du soleil : Wenn man Fixsterne sehr nahe an der Sonne beobachten konnte, so wurde man wohl darauf Rücksicht nehmen müssen (Si l’on pouvait observer des étoiles très proches du Soleil, il faudrait tenir compte de cet effet, tout en notant qu’en pratique l’amplitude est négligeable). Il ne figure aucune mention de la nécessité d’une éclipse solaire pour détecter et mesurer le phénomène. Pour Soldner le résultat obtenu ne souffre pas de doute, c’est une conséquence de la physique newtonienne, triomphante à cette époque, et l’important en est la conséquence pour les observations astronomiques. Il n’est pas question de tester une proposition théorique, mais de prendre en compte, potentiellement, un effet jusqu’ici négligé. Einstein va se trouver dans un tout autre contexte avec la prédiction relativiste.
La publication de Soldner a sombré dans l’anonymat le plus total et il est probable qu’il n’a pas été le seul à faire ce calcul. L’action de la gravitation étant indépendante de la masse, il s’imposait dans le cadre de la théorie corpusculaire. L’introduction du photon par Einstein et la quantification des échanges entre la lumière et la matière ont aussi ravivé l’analogie, mais durant le XIXe siècle la lumière est une onde et la gravité n’agit pas sur une onde. On pense aujourd’hui qu’Einstein ignorait ce résultat, et c’est une autre logique, celle du principe d’équivalence, qui l’a amené à sa propre estimation de l’effet de la gravitation sur la lumière et à aboutir au même résultat dans ses travaux préliminaires à la relativité générale en 1907 et 1911. Lorsque le résultat de Soldner est revenu à la surface, cette identité a servi de prétexte aux opposants d’Einstein pour l’accuser de plagiat et pour le discréditer comme scientifique. Mais l’identité n’était que superficielle et masquait une différence profonde sur les principes.
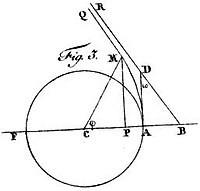
Figure 2 – Figure accompagnant l’article de Soldner pour expliquer son calcul de la déviation de la lumière par la gravitation solaire.
Nous en arrivons au calcul final d’Einstein, résultant de l’application des lois du mouvement dans la nouvelle théorie de la gravitation, telle qu’elle apparaît en novembre 1915 et dans le détail en 1916. Le cadre géométrique est maintenant complet et l’ensemble est plus riche que le simple principe d’équivalence. La déflexion prédite est maintenant de 1,75 seconde d’arc au lieu de 0,87, soit deux fois plus importante qu’en théorie newtonienne. Ce n’est pas une erreur de calcul qui aurait échappé à Einstein et qu’il a corrigée après quelques années. Non, le point important n’est pas tant l’importance de l’écart, mais l’existence d’une différence entre les deux prédictions. Il se trouve que le facteur deux est favorable à la détection, mais là n’est pas l’essentiel. La valeur d’Einstein n’est pas une correction à la prédiction issue de la gravitation de Newton, mais un résultat 100% différent, et constitue donc une prédiction critique permettant de trancher entre les deux théories, au moins sur ce point (le test sur la lumière est de ce point de vue moins important que celui du périhélie de Mercure qui dépend d’une prédiction plus spécifique à la théorie d’Einstein). Mais le calcul Newtonien appliqué à la lumière est totalement étranger à la théorie électromagnétique, tout comme la gravitation n’intervient nulle part dans la théorie de Maxwell.
Si ce calcul classique est sans aucun doute valable mathématiquement, rien ne garantit qu’il ait un sens physique. Le fait de calculer un angle de déviation qui ne dépend pas de la masse des particules, ne prouve en rien que la gravité agit sur la lumière. Ce n’est pas crucial pour la survie de la théorie. Dans la théorie de la relativité, il en va tout autrement, les principes concernant la structure de l’espace temps et la propagation de la lumière sont bien plus fondamentaux que les propriétés physiques de la lumière comme onde ou particule. Ce n’est plus l’action de la gravité sur la lumière qui est calculée mais la géométrie de la trajectoire lumineuse dans l’espace-temps. La lumière suit la courbure de cet espace et les effets observationnels ne sont plus identiques à ceux déduits d’une ligne droite ou courbe de l’espace euclidien. Ne pas voir la déviation des rayons lumineux prédits par le calcul classique ne remet absolument pas en cause la mécanique newtonienne, mais juste son application à un cas qui n’appartient pas au monde de cette théorie, surtout depuis que la lumière est devenue une onde. La déviation pourrait réellement être nulle dans ce cas, alors que pour la relativité générale, on toucherait au fondement même de la théorie : au principe d’équivalence et à la structure non euclidienne de l’espace-temps.
Ainsi il y a bien plus à tester qu’un facteur deux entre les deux prédictions, il s’agit d’une prédiction tout court, issue d’une nouvelle théorie. Il est presque plus important de constater qu’il y a une déviation, que d’obtenir un accord numérique avec la prédiction.
On peut aussi y voir un autre enjeu : admettons que l’observation confirme nettement la valeur classique. C’est bien entendu très gênant pour Einstein, mais dans le fond, c’est une nouvelle théorie, très exotique, qui doit faire ses preuves et beaucoup seront heureux qu’elle soit invalidée. Mais dans le même temps, ce serait un nouveau triomphe pour Newton, avec la preuve que la gravité agit sur les ondes lumineuses, comme si c’étaient des particules. Ce serait une question importante pour la physique, mais également une confirmation supplémentaire de l’universalité de la loi de la gravitation. Pour des Anglais affairés dans la préparation de l’expédition, c’est une affaire très sérieuse.
Préparation de l’expédition
L’éclipse de 1919 n’est pas la première tentative et l’idée de recourir à une éclipse remonte aux premiers calculs d’Einstein. On a tenté de profiter de l’éclipse du 10 octobre 1912 qui traversait le Brésil et dont la durée ne dépassait pas 2 minutes. Une expédition argentine et une américaine de l’observatoire de Lick s’y attellent mais l’observation n’a pas eu lieu en raison du mauvais temps. Les anglais étaient également présents à cette éclipse avec en particulier A. Eddington qui goûtait là à sa première entreprise astronomique de terrain, mais les objectifs n’étaient pas liés à la mesure de la déviation de la lumière.
La prochaine éclipse totale (durée 2min20s) a eu lieu le 21 août 1914, peu après le début de la première guerre mondiale. Les équipes allemandes qui s’y étaient préparées durent rebrousser chemin sur la route de la Crimée, après la déclaration de guerre entre l’Allemagne et la Russie.
Une belle éclipse au nord de l’Amérique du sud (Colombie, Venezuela) a lieu le 3 février 1916, puis une qui traverse les États-Unis le 8 juin 1918, mais de durée très courte, environ 1min20s durant cette phase proche de la fin de l’éclipse. En 1916 impossible d’organiser une expédition d’observation et aucun résultat exploitable n’est sorti des quelques clichés de celle de 1918.
On en arrive à la grande éclipse du 29 mai 1919, avec une durée approchant les 7min au maximum de l’éclipse, et 5min20s pour les lieux retenus. Cette éclipse ayant lieu fin mai, le Soleil se trouve dans la constellation du Taureau, très proche des Hyades, un champ dense riche en étoiles brillantes. La configuration est pratiquement idéale : longue éclipse, lieux accessibles qui ne sont pas perdus au bout du monde et un beau champ d’étoiles de référence. Une circonstance que l’on peut qualifier d’unique et qui ne se retrouvera pas avant longtemps.
Les éclipses suivantes ont lieu en 1921, sur la zone antarctique, et en 1922 sur l’Australie, avec une durée dépassant les 5 minutes. Cette dernière sera mise à profit pour confirmer le résultat de 1919, sans l’améliorer, mais pour l’heure, je me limite à l’éclipse historique de 1919.
Deux expéditions britanniques sont montées, initiées par l’astronome royal, et directeur de l’Observatoire de Greenwich, Franck Watson Dyson (1868-1938). L’une doit se rendre sur la côte nord-est du Brésil, à Sobral, et l’autre dans le golfe de Guinée, sur l’île de Principe de l’archipel Sao-Tomé et Principe (Figure 3). Andrew Crommelin (1865-1939) de l’Observatoire de Greenwich, est le chef de l’expédition du Brésil et, Arthur Stanley Eddington (1882-1944) directeur de l’Observatoire de Cambridge, celui de l’expédition africaine. Eddington est de loin le plus jeune, mais jouit déjà d’une notoriété certaine, après des études extrêmement brillantes à Cambridge et un passage par Greenwich.
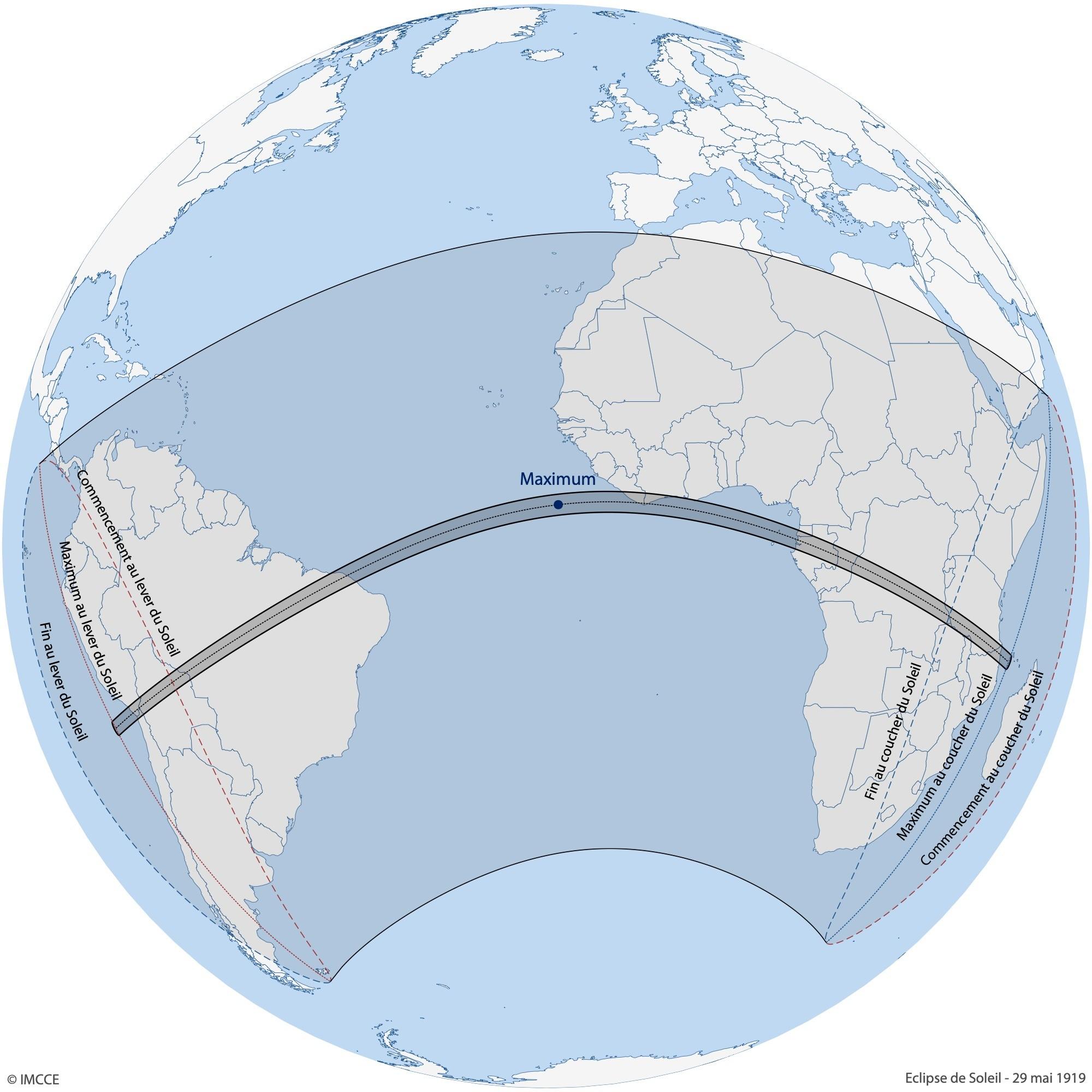
Figure 3 – Ligne de centralité de l’éclipse solaire du 29 mai 1919 (crédit : IMCCE)
Les astronomes ont été suffisamment convaincants lors de la défense de leur cause pour obtenir d’une même nation le financement de deux expéditions pour une campagne autour d’une éclipse de Soleil. C’est un fait inhabituel qui montre bien que l’enjeu est de taille. Et pourtant, l’objectif ne réside bien que dans cette mesure : il n’a pas été ajouté dans la proposition d’observations de physique solaire, d’étude de la couronne, pour muscler le projet et lui garantir un retour scientifique. Ce choix est délibéré et apparaît explicitement dans une communication d’Eddington publiée dans The Observatory : It is intended to concentrate entirely on the one problem of gravitation and light ; other eclipse problems can be postponed to a future occasion, but no equally favourable opportunity of measuring the deflection of light will occur for many years (L’intention est de se concentrer entièrement sur le seul problème de la gravitation et de la lumière ; les autres problèmes liés aux éclipses peuvent être reportés à une occasion ultérieure, mais aucune occasion aussi favorable de mesurer la déviation de la lumière ne se présentera avant de nombreuses années).

Figure 4 – Champ stellaire de la constellation du Taureau lors de l’éclipse du 29 mai 1919 à Principe. Les étoiles les plus brillantes sont de magnitude 5. Réalisé avec Sky Safari
Arthur Eddington est un excellent mathématicien et a eu l’opportunité de se plonger dans les premiers articles d’Einstein sur la théorie de la gravitation dès 1916 et d’en comprendre la portée. A cette date, ils sont peu nombreux à avoir cette expertise. Il a publié en 1918 (puis une seconde édition en 1920) un rapport sur la Théorie Relativiste de la Gravitation qui sera suivi en 1923 d’une monographie The Mathematical Theory of Relativity. Cet ouvrage, tout à fait lisible aujourd’hui, montre sa compréhension profonde de la théorie et sa maîtrise technique d’un nouvel environnement mathématique qu’il s’est approprié. En tant qu’ouvrage d’enseignement, il est demeuré pendant plusieurs décennies le seul exposé complet accessible aux chercheurs et à des étudiants avancés, à côté du Raum, Zeit Materie de H. Weyl publié à la même époque, mais plus difficile d’accès. Son ouvrage le plus célèbre et le plus utilisé dans la communauté astronomique demeure sans aucun doute le Internal constitution of stars publié en 1926 et qui a formé des générations d’astrophysiciens stellaires. Eddington n’est ni un observateur, ni un spécialiste des instruments astronomiques, mais un grand théoricien, et on peut être surpris de le voir en charge d’une mission de terrain aussi incertaine qu’exigeante.

Figure 5 – Arthur S. Eddington (1882-1944) autour de 1920.
Et effectivement la présence d’Eddington est le résultat d’un concours de circonstances tout à fait improbables, et en partie rendues possibles par la Guerre. Eddington vient d’une famille de Quakers, et est donc pacifiste et objecteur de conscience. Son pacifisme et l’absence de préjugés nationalistes ont peut être contribué à ce qu’il lise et mette en avant, dans le monde anglo-saxon, l’œuvre d’un savant allemand dès 1918. Il donnera plusieurs conférences à Cambridge et à la Royal Society sur la théorie d’Einstein. Toujours est-il que, pour lui éviter de partir au front ou d’être contraint à un service de soutien aux armées, F. Dyson prend sa plume pour appuyer la nécessité de maintenir Eddington dans ses activités en insistant sur le besoin impérieux de ses compétences pour une expédition de la plus haute importance : Newton ou Einstein, il en allait de l’intérêt national. Eddington obtient un report d’une année de son exemption de service et quelques mois plus tard l’Armistice est signée.
Le triple enjeu (Einstein, Newton ou autre chose) est bien perçu par Eddington comme on peut le voir sur la conclusion de sa publication dans The Observatory de mars 1919 (Figure 6).
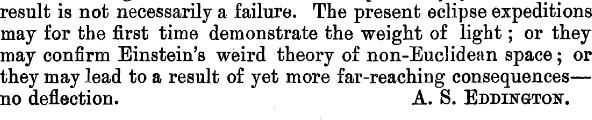
Figure 6 – Paragraphe de conclusion de l’article d’Eddington dans The Observatory dans lequel il présente l’expédition à venir et ses motivations.
Eddington embarque en mars 1919 pour le voyage vers le golfe de Guinée. Dans l’île de Principe, les astronomes sont équipés d’un astrographe et d’un lot de plaques photographiques. L’installation est prête dès le milieu du mois de mai. L’éclipse se déroule en début d’après-midi et toute la matinée du 29 se passe sous la pluie et le vent. Le ciel se dégage partiellement vers 13h, et c’est entre les nuages que les clichés, 16 au total, sont réalisés, sans vraiment savoir ce qu’il y a dessus. Eddington développe les plaques sur place et effectue les premières mesures de la position des étoiles sur deux plaques avant de rentrer en Angleterre. Il suspecte que le signal montre une déviation et qu’elle semble aller dans le sens de la valeur d’Einstein de 1916.
Les résultats
Ce n’est qu’après le retour des deux expéditions que l’analyse détaillée a pu être conduite par Dyson, Eddington et Davidson. Si les conditions météorologiques ont été difficiles en Afrique, cela n’a pas été le cas à Sobral où le ciel s’est bien dégagé lors de l’éclipse en milieu de matinée, ce qui permit de prendre plusieurs clichés durant les 5 min de la totalité. Il y avait deux astrographes sur place et sur l’un des deux on s’est rendu compte, après les observations, que la température avait modifié la mise au point, rendant les images diffuses et inexploitables pour des mesures de position. Heureusement, les plaques du deuxième instrument se sont avérées d’excellente qualité.
Les mesures des plaques faites en août 1919, donnèrent une déviation de 1,6 ± 0,30 seconde d’arc pour les données de Principe et 1,98 ± 0,12 seconde d’arc pour Sobral. La moyenne pondérée de l’ensemble des déterminations était de 1,65 seconde d’arc pour la déviation au limbe solaire. Après discussion des résidus et des diverses sources d’erreurs, le résultat final de la publication était 1,61 ± 0,30 seconde d’arc, accompagnée du commentaire essentiel suivant :… the accuracy seems sufficient to give a fairly trustworthy confirmation of Einstein’s theory, and to render the half-deflection at least very improbable (la précision semble suffisante pour donner une confirmation assez fiable de la théorie d’Einstein, et pour rendre la demi-déviation au moins très improbable). L’affaire semble entendue et penche fortement pour Einstein.
Dès le 27 septembre 1919, Einstein avait reçu le télégramme suivant de H. A. Lorentz :
Eddington found star displacement at the sun’s edge preliminary between nine-tenth second and double that. Many greetings. Lorentz (Eddington a trouvé que le déplacement des étoiles au bord du soleil était préliminairement entre neuf dixièmes de seconde et le double. Salutations. Lorentz).
Rien de final, mais suffisant pour anticiper les résultats officiels qui seraient révélés quelques semaines plus tard. L’information se propage dans le milieu universitaire berlinois à tel point qu’il reçoit les félicitations de Max Planck et d’autres collègues. La presse locale commence également à frémir.
Pour Einstein, une information plus certaine lui arrive lors d’un court séjour à Leyde, chez Lorentz. Le 23 octobre, l’astronome Hertzsprung lui fait part d’une lettre venant de Eddington indiquant que la mesure précise des plaques photographiques donne sa valeur théorique de la déviation de la lumière. Deux jours plus tard, lors d’une séance de l’Académie d’Amsterdam, Lorentz parle de la théorie de la relativité et des résultats des expéditions anglaises, tout en insistant sur le fait que ce sont des résultats provisoires.
Ces résultats furent annoncés de façon solennelle lors d’une réunion conjointe de la Royal Society et de la Royal Astronomical Society dans le bâtiment historique de Burlington House (Londres) le 6 novembre 1919, et sous forme finale (Figure 7) dans les Philosophical Transactions de la Royal Society. La salle était comble, l’ambiance électrique, et après l’annonce des résultats par Dyson, Crommelin, Eddington et la défaite de Newton, J.J. Thomson le célèbre physicien, prix Nobel et Président de la Royal Society, déclare : This is the most important result obtained in connection with the theory of gravitation since Newton’s day (Il s’agit du résultat le plus important obtenu en rapport avec la théorie de la gravitation depuis l’époque de Newton). La presse et le monde s’emparent de l’événement et, dès le lendemain, le Times de Londres titra Revolution in Science : New theory of the universe : Newtonian ideas overthrown (Révolution dans la science : Nouvelle théorie de l’univers : les idées newtoniennes renversées). Le New-York Times ne fut pas en reste, quelques heures plus tard, avec Lights all askew in the heavens : Einstein’s theory triumphs (Des lumières de travers dans les cieux : la théorie d’Einstein triomphe). Du jour au lendemain, A. Einstein était devenu une figure médiatique mondiale. Cette attention ne s’est pas démentie durant toute sa vie et son prestige bien au-delà.

Figure 7 – Page de titre et sommaire de l’article de Dyson, Eddington et Davidson sur la mesure de la déflexion de la lumière lors de l’éclipse totale de 1919. La publication contient la première observation de la déflexion de la lumière par le Soleil et sa mesure qui s’accorde avec les calculs d’Einstein.
Bien entendu, ce n’est pas la fin de l’histoire et tout le monde n’accepte pas ce résultat immédiatement. Comme dans toute série de mesures avec un signal relativement comparable à la précision, on peut discuter sans fin de la sous-estimation des erreurs, du choix des observations rejetées et de l’ampleur des effets systématiques. Les aspects parfois subjectifs de la pondération entre les deux sites d’observation furent aussi des arguments mis en avant par le camp du doute. Au-delà de la discussion scientifique, se mêlent à ces controverses, des relents anti-allemands, très ancrés juste après la Guerre, et des attitudes antisémites également à l’égard d’Einstein. Tout ceci est très documenté et a fait l’objet de recherches approfondies.
Toutefois, il est difficile d’accuser l’anglais Eddington d’avoir cherché à favoriser la valeur double par rapport à la valeur newtonienne, bien qu’il fût lui-même persuadé de la justesse de la théorie. Le traitement a été répété, examiné dans les moindres détails par la suite, tant que l’idée que le résultat n’était pas concluant restait vivace, et aujourd’hui les historiens s’accordent sur le fait que la barre d’incertitude est raisonnable.
Si l’on en était resté la, et surtout si le résultat n’avait pas été confirmé par la suite, mais bien des années plus tard, il est certain que cette expérience n’aurait pas la célébrité que l’histoire lui a confiée. Mais les éclipses suivantes, à commencer par celle de 1922, ont initialement plutôt confirmé l’accord avec la valeur d’Einstein et l’histoire, avide de simplification, retient avec de bonnes raisons que les mesures de Principe et de Sobral ont à elles seules consacré la théorie d’Einstein aux dépens de celle de Newton.
Cependant, cela n’a pas été un long fleuve tranquille et, dès 1929, et à plusieurs reprises par la suite, la valeur mesurée de la déflexion autour de 1,75 seconde d’arc a été remise en cause, et donc la confirmation expérimentale de la pertinence de la théorie de la gravitation d’Einstein comparée à celle de Newton. Certains résultats de mesure de la déviation semblent favoriser la valeur newtonienne, alors que d’autres étaient nettement plus élevés que la prédiction relativiste, et jetaient le doute sur le bien fondé de la théorie. Rien de totalement certain n’émerge avec les mesures optiques. Dans une lettre à Einstein de 1952 (lettre 98), Max Born s’interroge suite aux résultats divergents, on dirait réellement que ta formule n’est pas tout à fait exacte. Lors de la grande éclipse de 1973 le résultat n’est pas meilleur que 1,67 ± 0,2 seconde d’arc, soit une précision relative qui n’atteint pas 10%. Ce n’est que dans les années 1970 avec des mesures en ondes radio de la déviation au bord du Soleil, et l’arrivée du test de Shapiro sur les temps de parcours de la lumière que le consensus s’est réalisé en faveur de la Relativité Générale. D’autres succès allaient suivre et aujourd’hui ce sont des écarts à la théorie d’Einstein qui sont recherchés, mais jusqu’à maintenant sans succès.
Conclusion
On n’a pas fini de discuter du coût critique des observations de 1919 et de la confirmation, ou pas, des prédictions d’Einstein. Dans les manuels d’histoire des sciences, cette expérience est donnée comme exemple d’une expérience critique : une théorie est rejetée (Newton), une autre (Einstein) semble meilleure pour décrire la nature. Une théorie physique n’est pas vraie au sens mathématique du terme, elle est simplement plus juste à un moment donné pour expliquer les faits empiriques. Ce qui semblait être vrai au soir du 6 novembre 1919 (test critique), a été contesté quelques années plus tard. Même si les mesures récentes donnent raison à Eddington, cela n’efface pas cette longue période de doute, permettant à chaque camp de crier victoire, d’un côté ou de l’autre, au gré des mesures.
Le 6 novembre 1919 encore, la théorie de Newton, c’est à dire ses fondements, est en lambeaux. Cela ne l’empêche pas de rester pendant plusieurs dizaines d’années encore, le modèle quasi-parfait pour calculer avec une très haute précision les mouvements planétaires ou ceux des sondes spatiales. Les effets relativistes, nécessaires aujourd’hui, sont introduits dans un cadre newtonien, avec des termes correctifs dans la force ou le potentiel, et non avec tout l’habillage rigoureux des équations du mouvement relativiste. Donc même une théorie invalidée par les faits, peut conserver une très grande valeur pour comprendre la nature.
A mon avis, l’expérience de Principe et de Sobral, si elle n’est pas critique dans un sens épistémologique strict, mérite ce qualificatif dans le sens qu’elle a amené la relativité générale dans le monde des tests expérimentaux et lui a conféré le statut de théorie non spéculative. Pour la relativité générale (et pour Einstein) plus rien ne sera comme avant à partir de cette date. Si ce n’est pas une expérience critique, c’est bien une étape critique.
François Mignard, directeur de recherche au Laboratoire Lagrange de l’Observatoire de la Côte d’Azur
