L’âge du Système solaire est aujourd’hui estimé à 4,567 milliards d’années. La détermination de cet âge, ainsi que les datations d’autres événements très anciens ont été rendues possibles grâce à la mise au point de chronomètres géochimiques très précis basés sur la désintégration de certains isotopes radioactifs.

Vue d’artiste de la nébuleuse protosolaire. (Crédit : NASA/JPL-Caltech)
On sait aujourd’hui que la Terre est âgée d’environ 4,55 milliards d’années (Ga). La naissance du Système solaire est nécessairement antérieure, et on l’estime à 4,567 Ga (un chiffre particulièrement facile à retenir…). À l’échelle de la vie humaine, ou même de la durée d’une civilisation, il est difficile d’imaginer ce que représentent ces âges plus que canoniques. Et comme pour accentuer le caractère insondable de ces durées, on ne disposait pas, jusque vers le début du xxe siècle, de méthode fiable pour les évaluer. Comme nous allons le voir, les datations du Système solaire, de la Terre, ainsi que celles d’autres événements très anciens découlent de la découverte de la radioactivité au tournant des xixe et xxe siècles. Toutefois, si les scientifiques ont vite compris qu’ils pourraient établir des chronomètres à partir de la désintégration radioactive de certains éléments, la mise au point de ces chronomètres a pris plusieurs décennies [1], et la précision actuelle des mesures nécessite des appareils extrêmement performants.
Isotopes radioactifs et chronomètres géochimiques
Avant d’entrer plus en détail dans les méthodes de datation, il est important de revenir sur la notion d’isotope radioactif. Rappelons pour commencer que les isotopes d’un élément donné sont des atomes qui possèdent le même nombre de protons (et donc le même numéro atomique, qui définit l’élément en question), mais un nombre de neutrons différent, et donc une masse différente. Certains isotopes sont instables, c’est-à-dire qu’ils se transforment en un autre élément (leur numéro atomique change) soit par émission d’un noyau d’hélium (radioactivité α ; le numéro atomique de l’élément diminue de deux unités), soit par transformation d’un neutron en proton avec émission d’un électron (radioactivité β–, l’isotope « monte » d’un numéro atomique) ou d’un proton en neutron avec émission d’un positron (radioactivité β+ ; l’isotope « descend » un numéro atomique). C’est par exemple le cas du célébrissime isotope 14C du carbone (qui se désintègre par radioactivité β–), ainsi que des isotopes 26Al de l’aluminium (radioactivité β+), 40K du potassium (radioactivité β– et β+) et de tous les isotopes de l’uranium, dont le 235U et le 238U (radioactivité α). On ne peut pas prédire quand exactement un noyau particulier va se désintégrer. En revanche, on peut calculer précisément le temps nécessaire pour que la moitié d’une population initiale d’isotopes d’un élément donné se désintègre. Ce temps, appelé demi-vie, est différent pour chaque isotope. Il est par exemple de 5 700 ans pour le 14C et de 717 000 ans pour l’26Al, ce qui peut sembler très long, mais est très court à l’échelle des temps géologiques et en comparaison des demi-vies du 238U (0,7 Ga), du 40K (1,25 Ga) et du 238U (4,47 Ga) [2].
C’est cette propriété statistique : la demi-vie étant à la base des méthodes de datation (on parle aussi de chronomètre) géochimique, l’idée est que, si l’on connaît la quantité d’un isotope dans un échantillon de roche (ou autre) à l’instant où l’événement que l’on souhaite dater se produit, on peut, en mesurant la quantité de cet isotope encore présente aujourd’hui, en déduire le temps écoulé depuis cet événement (fig. 1). En fonction de l’ancienneté supposée d’un événement, on aura recours à des isotopes (chronomètres) de demi-vie plus ou moins longue. Le 14C est très prisé par les archéologues, car il permet de dater des échantillons préhistoriques (os, bois ou tout autre résidu de matière organique) jusqu’à environ 50 000 ans dans le passé. Pour les événements géologiques remontant à des millions, voire des milliards d’années, il faudra faire appel à des chronomètres impliquant des isotopes à longue durée de vie, comme les isotopes de l’uranium (235U et 238U), le 40K ou encore l’isotope 87Rb du rubidium, dont la demi-vie est de 49,7 Ga. Dit comme cela, tout paraît simple. Ça l’est beaucoup moins en pratique, la difficulté principale (mais pas unique) étant de déterminer les teneurs initiales des isotopes impliqués dans les chaînes de désintégration que l’on souhaite utiliser. Pour contourner cette difficulté, les scientifiques ont recours à différentes astuces. Avant d’illustrer cela avec un chronomètre particulièrement important, remontons le temps jusqu’au début du xxe siècle.
-
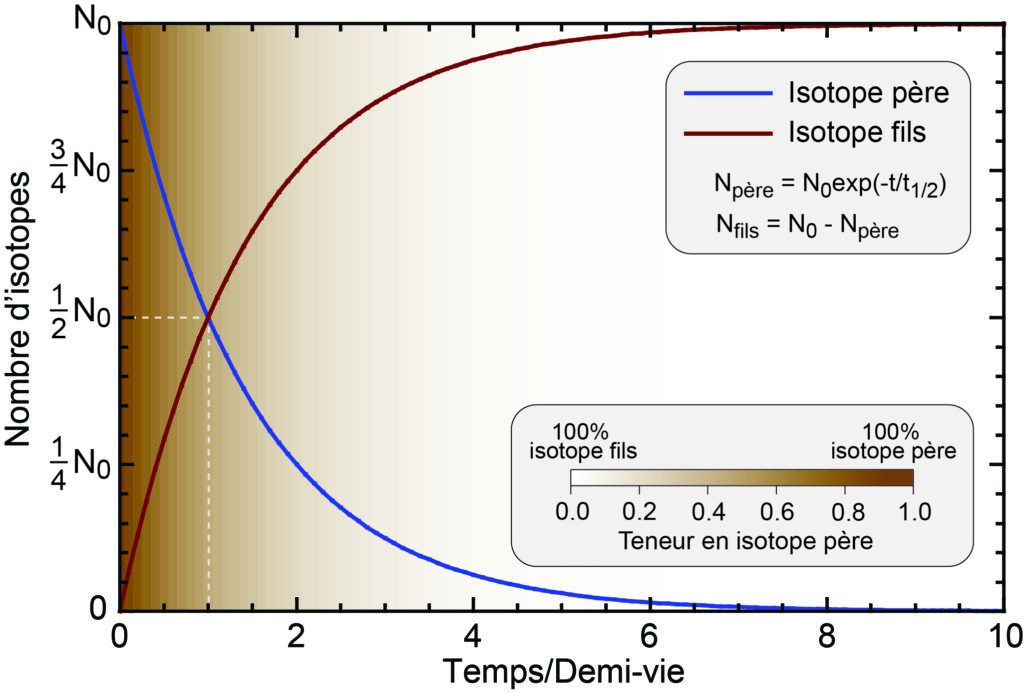
1. Décroissance radioactive d’un isotope père (courbe bleue) en un isotope fils (courbe rouge). L’axe des abscisses est gradué en unités de temps divisé par la demi-vie de l’isotope père, et le fond de couleur représente la teneur en élément père en fonction du temps. Le nombre d’isotopes pères diminue exponentiellement au cours du temps à partir d’une population initiale (de N0 atomes dans cet exemple). Ce nombre est divisé par deux après un temps égal à une demi-vie de l’isotope père (ligne en tirets), et au bout d’un temps égal à une dizaine de fois cette demi-vie, l’isotope père a quasiment disparu tandis que le nombre d’isotopes fils est très proche de N0. (Crédit : Frédéric Deschamps)
Un peu d’histoire
C’est Pierre Curie qui, le tout premier, a compris que la radioactivité pourrait être utilisée pour dater les roches de façon absolue. En 1902, alors que ce phénomène venait juste d’être découvert, il avait en effet remarqué que l’activité du radium diminuait de moitié tous les 4 jours environ [3]. Ernest Rutherford et Frédéric Soddy lui ont vite emboîté le pas, d’une part en montrant que le phénomène de radioactivité correspond à la transformation d’un élément père en un élément fils accompagnée de l’émission d’une particule énergétique (par exemple, un noyau d’hélium dans le cas de la radioactivité α), d’autre part en définissant le concept de demi-vie. Ils identifient également des chaînes de désintégration radioactives (plus précisément certaines étapes de celles-ci), en particulier celles de l’uranium et du thorium. En 1905, ces découvertes amènent Robert Strutt (Lord Rayleigh) à proposer une méthode de datation basée sur la mesure de la quantité d’hélium contenu dans les roches, méthode vite abandonnée, car il s’aperçoit que l’hélium contenu dans les roches peut facilement s’échapper vers l’atmosphère. De son côté, Bertram Boltwood parvient à établir que le produit final de la désintégration de l’uranium est le plomb. Il en déduit que la mesure des teneurs en ces éléments dans une roche devrait permettre de dater cette dernière. Les mesures qu’il réalise sur différents types de roches s’échelonnent entre 400 millions d’années (Ma) et 2,2 Ga. Un peu plus tard, entre 1908 et 1913, Soddy identifie des étapes supplémentaires des chaînes de désintégration, et propose le concept d’isotope, concept rapidement validé, notamment pour l’uranium et le plomb. Les travaux de Soddy ont aussi permis de clarifier les chaînes de désintégration radioactives en identifiant certains produits de ces chaînes à des isotopes d’éléments déjà connus [4]. Tous les ingrédients (ou presque) sont désormais en place pour mettre au point les méthodes de datation radioactive fiables et établir des échelles de temps géologiques (et planétologiques) absolues.
C’est à cela que s’attachera le géologue Arthur Holmes (fig. 2) pendant plus de trois décennies [5]. Dès 1911, Holmes entreprend de dater, à l’aide du chronomètre uranium-plomb (U-Pb), les roches caractéristiques des différentes strates (ou couches) géologiques. Jusqu’à l’avènement des datations radiochronologiques, la succession de ces couches offrait une chronologie relative permettant de classer les événements du plus jeune au plus ancien, mais pas de donner un âge à la Terre. En 1935, Holmes publie une échelle absolue jusqu’au début du Cambrien (qu’il estime à 510 Ma ; à comparer avec la valeur aujourd’hui admise de 542 Ma). Il remarque aussi que certaines roches (précambriennes) sont âgées de 1,9 Ga et plus, et que par conséquent la Terre et le Système solaire sont encore plus vieux. Toutefois, la précision de la méthode utilisée par Holmes repose sur l’hypothèse que tous les isotopes du plomb sont issus de désintégrations radioactives, ce qui est inexact. À partir des années 1940, géologues et physiciens cherchent donc un moyen de contourner ce problème. Holmes remarque qu’en utilisant conjointement les chaînes de désintégration des isotopes 235U et 238U, qui aboutissent chacune à un isotope différent du plomb, il est possible de déduire un temps absolu sans que l’on ait besoin de connaître les teneurs initiales relatives en ces isotopes. C’est essentiellement cette idée qui est mise en œuvre dans le chronomètre Pb-Pb (plomb-plomb), que nous allons maintenant décrire plus en détail.

2. À partir du chronomètre uranium-plomb (U-Pb), Arthur Holmes (en haut) a réalisé les premières datations absolues des séquences stratigraphiques établies par les géologues. Vers le milieu des années 1940, il a également développé le chronomètre plomb-plomb (Pb-Pb), simultanément et indépendamment mis au point par le physicien Friedrich Houtermans. Vers le milieu des années 1950, le géochimiste Clair Patterson (en bas) a affiné les méthodes de mesure, ce qui lui a permis de déterminer l’âge de la Terre en appliquant le chronomètre Pb-Pb aux météorites de Canyon Diablo. (Crédits : Geological Society of Glasgow et California Institute of Technology)
Le chronomètre Pb-Pb
Le chronomètre Pb-Pb, mis au point simultanément et indépendamment par Arthur Holmes et par le physicien Friedrich Houtermans dans les années 1940, est l’un des chronomètres les plus utilisés par les scientifiques pour dater les roches. Comme il est basé sur la désintégration des isotopes 235U et 238U de l’uranium (dont on a vu que les demi-vies sont très longues), ce chronomètre est particulièrement adapté à la datation des événements très anciens. Ainsi, c’est ce chronomètre que Clair Patterson (fig. 2) a utilisé en 1956 pour déterminer l’âge de la Terre à partir des météorites de Canyon Diablo. Il a également été utilisé pour dater les échantillons de roches lunaires rapportés par les missions Apollo et, plus récemment, par la sonde chinoise Chang’e-5. Pour contourner le problème des teneurs initiales en éléments père et fils (ici, les isotopes de l’uranium et du plomb), la méthode Pb-Pb combine deux chaînes de désintégrations radioactives (fig. 3) : d’une part, la désintégration de 235U en 207Pb via une dizaine de désintégrations intermédiaires, et d’autre part la désintégration de 238U en 206Pb, en passant, là aussi, par une quinzaine de réactions intermédiaires. Les isotopes 207Pb et 206Pb, dont on mesure les teneurs actuelles dans l’échantillon (roche terrestre ou météorite) que l’on souhaite dater, sont, évidemment, tous deux stables. Chacune de ces deux chaînes radioactives fait intervenir de nombreux isotopes intermédiaires, tous radioactifs, mais de demi-vies très inférieures aux demi-vies de 235U et 238U. Autrement dit, c’est la première étape de chacune de ces chaînes (désintégrations de 235U en 231Th, et de 238U en 234Th) qui contrôle les temps nécessaires à la formation et l’accumulation de 207Pb et 206Pb dans les roches. L’astuce consiste à mesurer aussi la teneur en 204Pb, un autre isotope du plomb, puis à calculer les rapports d’abondance 207Pb/204Pb et 206Pb/204Pb. Le 204Pb est lui aussi stable et surtout il n’est le produit d’aucune chaîne de désintégration radioactive. Sa teneur est donc restée la même au cours du temps, depuis la formation de la roche et jusqu’au moment de la mesure. Les mesures des teneurs en 204Pb, 206Pb et 207Pb sont ensuite répétées en différents points (minéraux) de la roche. On obtient alors des valeurs des rapports 207Pb/204Pb et 206Pb/204Pb a priori différentes pour chaque point, mais qui doivent s’aligner le long d’une droite. Cela tient au fait que lors de la formation de la roche, l’abondance totale en plomb (c’est-à-dire la somme des abondances de tous les isotopes de cet élément) a pu varier d’un endroit à l’autre de cette roche, tandis que les abondances relatives de chaque isotope étaient, elles, constantes. On peut alors montrer que la pente de cette droite ne dépend que du rapport actuel entre les isotopes 235U et 238U (235U/238U, lequel est remarquablement constant à 1/137,88 d’une roche ou d’une météorite à l’autre), et… du temps écoulé depuis la formation de la roche. La mesure de la pente de la droite 207Pb/204Pb vs 206Pb/204Pb, que l’on appelle aussi isochrone, permet ainsi de mesurer l’âge d’une roche. À noter que certains travaux préfèrent représenter 207Pb/206Pb en fonction de 204Pb/206Pb : la présentation est différente, mais la méthode reste la même.
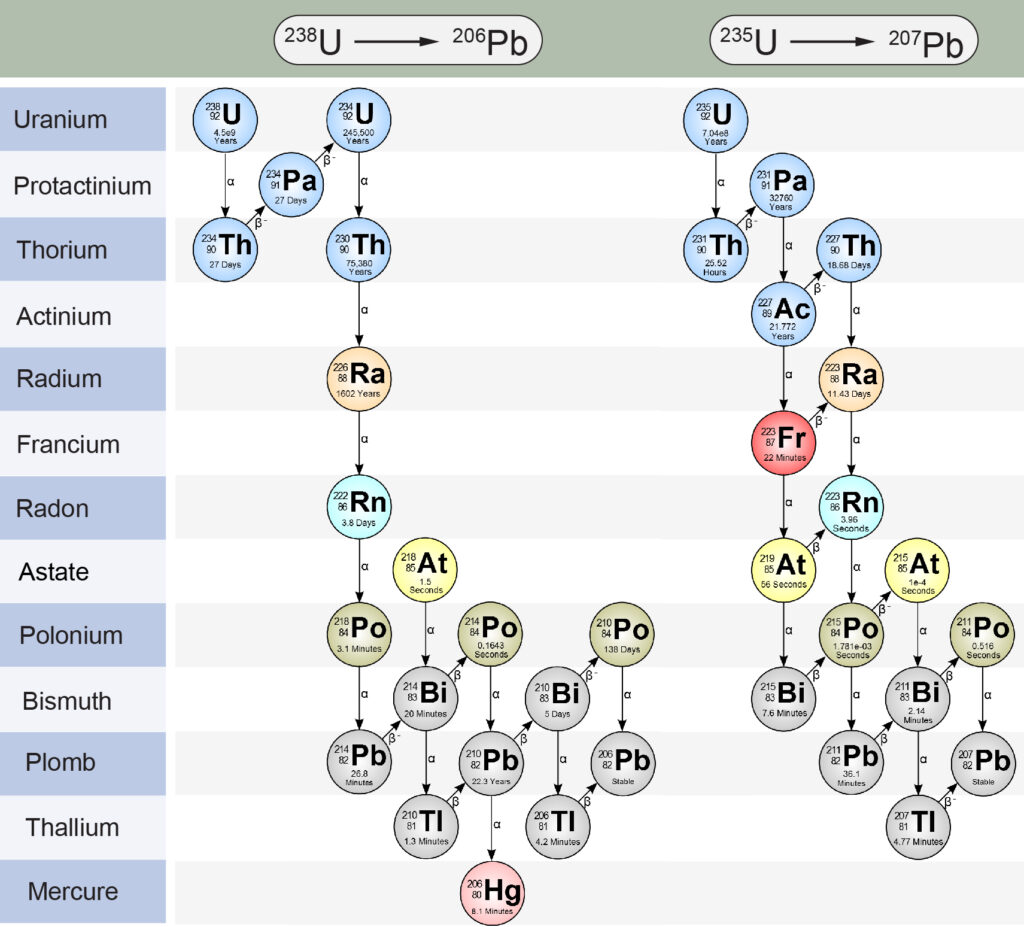
3. Les chaînes de désintégration radioactives du 238U vers le 206Pb et du 235U vers le 207Pb impliquées dans le chronomètre Pb-Pb. Chacune de ces chaînes fait intervenir une succession de désintégrations α (émission d’un noyau d’hélium) et β– (transformation d’un neutron en proton), avec des demi-vies différentes (temps indiqué au bas de chaque case). Les demi-vies du 238U et du 235U étant beaucoup plus longues que celles des autres isotopes impliqués, la durée totale nécessaire pour aboutir au 206Pb et au 207Pb est largement dominée par la première désintégration de chaque chaîne (238U en 234Th et du 235U en 231Th). (Crédit : modifié d’après Washington University in St-Louis)
L’âge du Système solaire
Il est maintenant temps de répondre à la question posée dans le titre de cet article. Le petit détour par le chronomètre Pb-Pb n’aura pas été inutile, car c’est précisément avec cette méthode appliquée aux inclusions calcium-aluminium (les fameuses CAI ; fig. 4) contenues dans certaines chondrites carbonées que plusieurs équipes ont pu, au début des années 2010, déterminer l’âge du Système solaire (fig. 5). Comme leur nom l’indique, les CAI sont composées de minéraux riches en calcium et en aluminium, qui sont très réfractaires (au sens physique de ce terme), car ils condensent à des températures supérieures à 1 700 K. C’est pourquoi on pense que ces grains sont les premiers matériaux à avoir condensé dans la nébuleuse protosolaire, et que cela a dû se produire très peu de temps après l’allumage du Soleil, alors que ce dernier était très actif. Par extension, leur formation est un excellent jalon pour dater la naissance du Système solaire, et ce d’autant plus que l’on peut, grâce au chronomètre Pb-Pb, mesurer leur âge de façon absolue.
D’autres systèmes isotopiques que le chronomètre Pb-Pb ont également été utilisés pour dater les CAI. Ceux-ci parviennent à des résultats quasiment identiques. Par exemple, le chronomètre néodyme-uranium (Nd-U), qui représente le rapport 235U/238U en fonction du rapport 144Nd/238U, donne un âge légèrement supérieur (4,566 Ga), mais compatible avec les âges prédits par le chronomètre Pb-Pb. Les barres d’erreur sur les mesures (que l’on oublie parfois de mentionner) sont de quelques centaines de milliers d’années, donc très petites. Cette précision élevée est l’occasion de dire un mot sur les mesures des rapports isotopiques elles-mêmes. Celles-ci sont réalisées avec des spectromètres de masse (fig. 6), dont le principe est de séparer les ions contenus dans un gaz ou un fluide en fonction de leur masse (plus exactement en fonction du rapport entre leur masse et leur charge électrique, m/q), d’abord en les accélérant grâce à un champ électrique, puis en les faisant passer à travers un champ magnétique avant de les envoyer vers un réseau de détecteurs. La trajectoire de ces ions est fonction du rapport m/q, si bien que des ions de masses différentes arrivent sur différents détecteurs. On peut ainsi compter les quantités respectives de différents isotopes (ionisés) contenus dans un matériau donné, et déterminer la composition isotopique de ce matériau. Lorsque l’on souhaite déterminer l’âge d’un échantillon rocheux, il faut au préalable ajouter un système de chauffage permettant de vaporiser et d’ioniser cet échantillon. Les isotopes des éléments impliqués dans les chronomètres géochimiques sont souvent présents en très petites quantités (quelques millionièmes de la masse totale). Cela nécessite des mesures très précises, auxquelles les spectromètres de masse modernes ont accès.

4. Détail de la météorite d’Allende montrant des inclusions riches en calcium et en aluminium (CAI). (Crédit : G. J. McPherson et A. Boss, 2011)
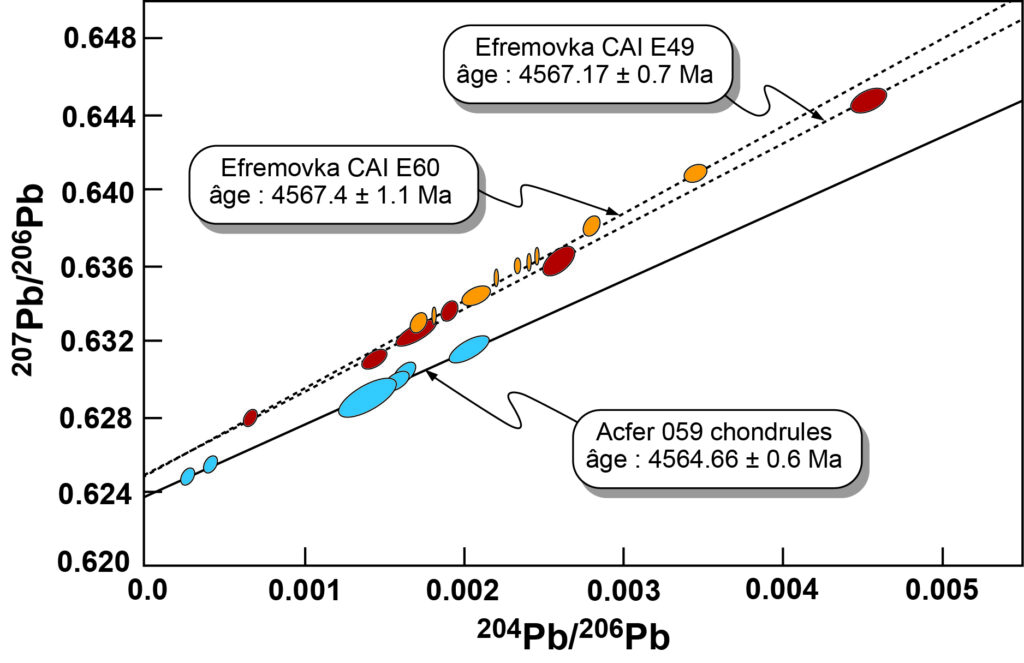
5. Détermination de l’âge du Système solaire à partir de la mesure des rapports isotopiques du plomb (chronomètre Pb-Pb) dans les inclusions calcium-aluminium (CAI) de météorites chondrites carbonées (ici Efremovka). Les mesures effectuées sur différents échantillons d’une CAI donnée s’alignent le long d’une droite dont la pente permet de déterminer l’âge de cette CAI. Les âges mesurés pour deux CAI de la météorite Efremovka sont quasiment identiques, à 4,567 Ga. La datation de chondrules dans d’autres météorites (ici Acfer), toujours avec le chronomètre Pb-Pb, montre que ces chondrules sont plus jeunes que les CAI de quelques millions d’années. (Crédit : Amelin et al., 2010)
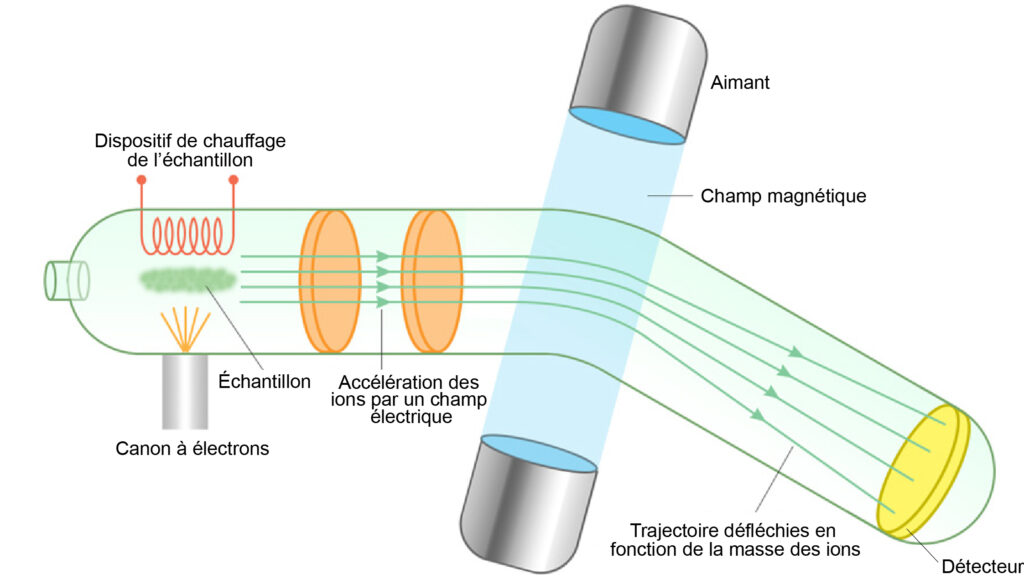
6. Principe du spectromètre de masse. Cet appareil permet de séparer des ions de masses différentes en les accélérant avec un champ électrique, puis en les soumettant à un champ magnétique qui défléchit leur trajectoire en fonction de leur masse (les masses les plus faibles subissant une déflexion plus importante). (Crédit : ChemistryLearnier.com)
Le chronomètre Pb-Pb est très utile, car il permet de déterminer l’âge absolu d’une roche ou d’une météorite. Pour reconstruire l’histoire du Système solaire, les scientifiques ont aussi mis au point des chronomètres relatifs, qui permettent de mesurer le temps écoulé entre deux événements particuliers dont on ne connaît pas forcément l’âge absolu. On peut comparer les chronomètres relatifs à un sablier : on ne sait pas exactement quand le sablier a été retourné, mais on connaît très précisément le temps nécessaire pour qu’une quantité de sable donnée s’écoule du compartiment du haut vers le compartiment du bas. L’avantage des chronomètres relatifs est qu’ils peuvent s’appuyer sur des isotopes de demi-vie relativement courte (quelques millions d’années ou moins) présents dans les matériaux primitifs du Système solaire. Ces isotopes sont aujourd’hui éteints, mais ils ont laissé des signatures, sous forme d’éléments fils, dans les roches. Par exemple, en mesurant la quantité de ces éléments fils dans deux échantillons d’âges a priori différents, on peut mesurer le temps écoulé entre les formations de ces deux échantillons. Prenons deux exemples concrets. Le premier exemple est basé sur l’isotope 26Al de l’aluminium et permet de poser une limite supérieure au temps écoulé entre l’explosion de la supernova qui a ensemencé le Système solaire (et dont les ondes de choc ont sans doute provoqué la contraction du nuage de gaz qui en est à l’origine) et la formation des premiers matériaux de ce Système. L’26Al est essentiellement produit dans les supernovæ, et il se désintègre en 26Mg, le second isotope le plus abondant du magnésium. Sa demi-vie est relativement courte, 717 000 ans, si bien qu’une population initiale d’26Al est considérée comme éteinte au bout d’une dizaine de millions d’années. La présence de 26Mg dans les météorites est en soi un indice que le Système solaire s’est formé très rapidement et peu de temps après l’explosion de la supernova, quelques dizaines de millions d’années au plus, car il indique que de l’26Al était bien présent au moment où ces météorites se sont formées. Bien sûr, il faut tenir compte du fait que du 26Mg était déjà présent lors de la formation du Système solaire et a été lui aussi incorporé dans les météorites. Pour cela les géochimistes mesurent les rapports 26Mg/24Mg et 27Al/24Mg et représentent dans un graphique le premier en fonction du second. L’alignement de ces mesures le long d’une droite indique un enrichissement en 26Mg par rapport à une valeur que l’on ne connaît pas forcément, et donc la présence initiale d’26Al. Le second exemple implique les isotopes 182Hf de l’hafnium et 182W du tungstène, et permet de dater la formation des noyaux planétaires (figure). Le 182Hf se désintègre en 182W avec une demi-vie de 8,9 millions d’années, donc, là encore, relativement courte. Par ailleurs, l’hafnium est lithophile, c’est-à-dire qu’il se lie préférentiellement avec les roches, tandis que le tungstène est, au contraire, sidérophile, c’est-à-dire qu’il se lie avec le fer. Lors de la formation du noyau, le fer va entraîner avec lui le tungstène présent à cet instant vers le centre de la planète (ou du planétésimal), mais pas l’hafnium. Si le noyau se forme tardivement (100 millions d’années ou plus), toute la population de 182Hf initialement présente aura, au moment de cette formation, eu le temps de se désintégrer en 182W. Ce dernier sera alors entraîné par le fer dans le noyau, et il n’en restera presque plus dans le manteau. À l’inverse, dans le cas d’une formation précoce, du 182Hf sera toujours présent dans le manteau après que le noyau se sera formé, et sa désintégration y produira, par la suite, du 182W. La quantité de 182W présente aujourd’hui dans le manteau terrestre (ou dans les météorites qui sont issues des manteaux des planétésimaux) permet donc d’estimer à quel moment planètes et planétésimaux se sont différenciés. Les mesures montrent que cela s’est produit assez tôt dans l’histoire du Système solaire, entre 30 et 40 Ma après la formation des inclusions calcium-aluminium (CAI).
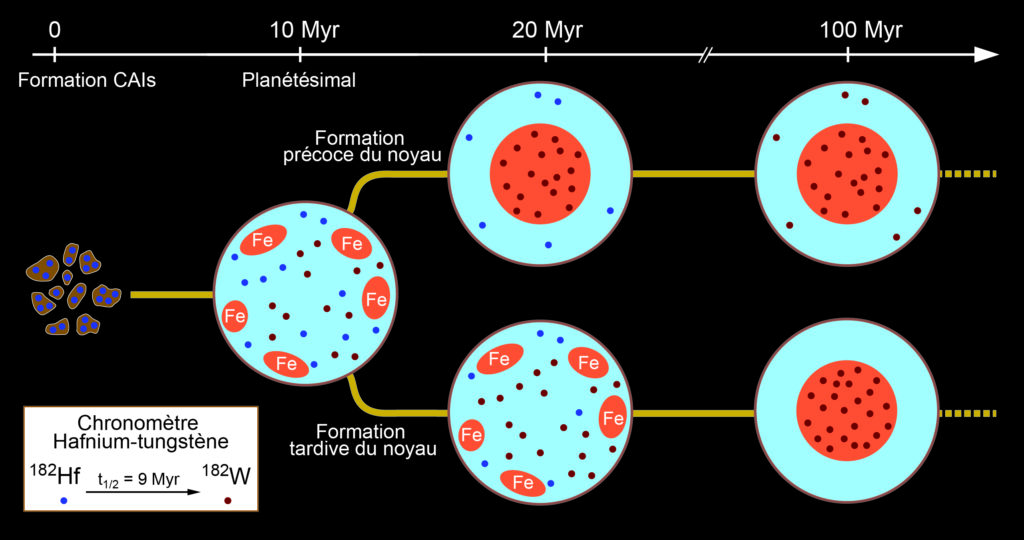
Le chronomètre hafnium-tungstène et la formation des noyaux planétaires. Lors de leur formation, les planétésimaux contiennent une certaine quantité de l’isotope 182Hf du hafnium. Ce dernier est instable et se désintègre en 182W du tungstène avec une demi-vie de 9 millions d’années (Myr). Il disparaît entièrement en environ 100 Myr. Le tungstène est sidérophile, c’est-à-dire qu’il se lie facilement avec le fer et qu’il est entraîné par celui-ci lors de la formation du noyau. L’hafnium, à l’inverse, est lithophile et reste dans le manteau. Selon la quantité de 182W présente dans les météorites rocheuses (issues du manteau des planétésimaux), on peut estimer combien de temps après la formation des inclusions calcium-aluminium (CAI) les noyaux des planétésimaux et des planètes rocheuses se sont formés. Les mesures actuelles montrent que ces formations se sont produites entre 30 et 40 Myr après la formation des CAI. (Crédit : F. Deschamps)
L’âge du Système solaire, vraiment ?
Revenons un instant sur l’hypothèse que les CAI se sont formées au tout début de l’histoire du Système solaire, très peu de temps avant que le Soleil ne s’allume. Cette hypothèse est confortée par d’autres indices de nature géochimique, en particulier le fait que certaines CAI présentent une quantité anormalement élevée de l’isotope 10B du bore, liée la désintégration de l’isotope 10Be du béryllium. Le 10Be, dont la demi-vie est relativement courte (1,39 million d’années), résulte lui-même de la spallation (ou décomposition) d’éléments plus lourds sous l’effet de rayonnements à haute énergie, par exemple de rayons X émis par les très jeunes étoiles, avant qu’elles ne rejoignent la séquence principale (phase T Tauri). La présence de 10Be dans les CAI suggère ainsi que ces grains se sont formés à une époque où le Soleil était lui-même au stade T Tauri.
Reste que l’on peut, avec raison, vouloir discuter la façon de définir l’âge du Système solaire ou même celui de la Terre. Les formations de l’un et de l’autre ne sont pas des événements ponctuels, mais comportent plusieurs phases qui s’inscrivent elles-mêmes dans la durée. Ce sont, dans le premier cas, la contraction d’un nuage de gaz, la formation et l’allumage d’une protoétoile en son centre, puis le passage de cette étoile par la phase T Tauri avant qu’elle n’accède à la séquence principale, la condensation de résidus dans le disque protoplanétaire et l’assemblage (l’accrétion) de ceux-ci en planétésimaux. Dans le second cas, la formation de « briques » fondamentales (dont les météorites sont les résidus), l’accrétion de ces briques pour former une proto-Terre, la différenciation de celle-ci en un noyau et un manteau, et sa collision avec une planète plus petite (Théia). Quels événements retenir pour définir la naissance du Système solaire et celle de notre planète ? Pourquoi la formation des CAI dans le premier cas et celle des météorites chondrites carbonées dans le second ? Une manière de répondre à cette question (ou de la contourner) est de remarquer que les séquences d’événements que l’on vient d’esquisser se sont déroulées dans des laps de temps relativement brefs, quelques millions à quelques dizaines de millions d’années. Autrement dit, un mouchoir de poche à l’échelle des temps géologiques. Plusieurs éléments ont permis d’établir cette chronologie, notamment, et là aussi, la mesure des rapports d’abondance de certains isotopes, utilisés cette fois-ci pour définir des échelles de temps relatives (encadré). Par ailleurs, les modèles d’évolution stellaire estiment la durée des phases de contraction du nuage initial et d’allumage de l’étoile à quelques centaines de milliers d’années au total, et celle de la phase T Tauri (au cours de laquelle les CAI se sont formées) à quelques millions d’années. Enfin, l’observation directe (en infrarouge) de planètes dans les disques protoplanétaires de très jeunes étoiles (quelques millions d’années) conforte l’idée que, dans sa prime jeunesse, le Système solaire a évolué très rapidement. Dans ce contexte, la formation des CAI, dont l’âge fournit la datation absolue la plus ancienne et la plus fiable que l’on puisse effectuer, est effectivement un bon point de repère pour dater la formation du Système solaire.
Frédéric DESCHAMPS | IESAS, Taipei, Taïwan
Notes
- Voir à ce sujet les trois derniers chapitres de l’excellent livre de Pascal Richet L’Âge du monde – À la découverte de l’immensité du temps, aux éditions du Seuil. Les lecteurs anglophones pourront aussi se tourner vers The Chronologers’ Quest – The Search for the Age of the Earth, de Patrick Wyse Jackson, paru chez Cambridge University Press.
- À l’inverse, d’autres isotopes ont une demi-vie beaucoup plus courte, par exemple de l’ordre de la seconde pour les isotopes 207Ra et 208Ra du radium, et de quelques milliardièmes de seconde pour certains isotopes exotiques.
- Il s’agissait de l’isotope224Ra, dont la demi-vie est plus précisément de 3,6319 jours.
- Par exemple le thorium-X, première étape de la décroissance du 232Th (dont la demi-vie est de 14,1 Ga), et qui est en fait l’isotope 228Ra du radium, lui-même instable avec une demi-vie de 5,7 ans.
- Arthur Holmes est également le promoteur de l’idée que le manteau terrestre est animé de grands mouvements de convection, en notant qu’en surface, ce mécanisme permet d’entretenir la dérive des continents.

Publié dans le magazine l’Astronomie
